пр5_190
.docxМИНОБРНАУКИ РОССИИ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)
Кафедра ИС
ОТЧЕТ
по лабораторной работе №5 по дисциплине «ИКСиС» Тема: «Формулы Эрланга» Вариант №190
Студент
гр.
Преподаватель Воробьёв А.И.
Санкт-Петербург 2023
Цель работы:
Изучить первую и вторую формулы Эрланга.
Написать программу, реализующую первую формулу Эрланга.
Построить график зависимости вероятности блокировки заявок от интенсивности поступающей нагрузки при числе обслуживающих устройств 2 * n.
Построить график зависимости вероятности блокировок заявок от числа обслуживающих устройств при интенсивности поступающей нагрузки n.
Написать программу, реализующую вторую формулу Эрланга.
Построить график зависимости вероятности ожидания начала обслуживания и средней длины очереди от интенсивности поступающей нагрузки при числе обслуживающих устройств 2 * n.
Построить график зависимости вероятности ожидания начала обслуживания и средней длины очереди от числа обслуживающих устройств при интенсивности поступающей нагрузки n.
Ход выполнения работы: Листинг программного кода 1:
Реализация первой и второй формул Эрланга
1.
import
math
2. import matplotlib.pyplot as plt
3. import numpy as np
4.
5. def erlang_one(A, N):
6. p = 1
7. for i in range(1, N):
8. p = A * p / (i + A * p)
9. return p
10.
-
11. def
erlang_two(A, N):
12.
E = erlang_one(A,
N)
13.
p = (E) / (1 - (A
/ N) * (1 - E))
14.
return p
15.
16. def
queue(A, N):
17.
E = erlang_one(A,
N)
18. n = (N / (N - A)) * ((A * E) / ((N - A) + A * E))
19. return n
Листинг программного кода 2:
Реализация
выводов графиков
1. def |
plot_blocking_probability_A(A_values, N): |
|
2. |
blocking_probabilities = [erlang_one(A, N) for |
A in A_values] |
3. |
|
|
4. |
plt.plot(A_values, blocking_probabilities) |
|
5. |
plt.xlabel('Интенсивность поступающей нагрузки |
(A)') |
6. |
plt.ylabel('Вероятность блокировки (P)') |
|
7. |
plt.title(f'Зависимость вероятности блокировки |
от интенсивности |
нагрузки\nЧисло обслуживающих устройств (N) = {N}')
8. plt.grid(True)
9. plt.show()
10.
11. N_value = 2 * 190 # Число обслуживающих устройств
12. A_values = np.linspace(0.1, 1000, 50) # Интенсивность нагрузки
13.
14. plot_blocking_probability_A(A_values, N_value)
1.
def
plot_blocking_probability_N(N_values,
A):
2. blocking_probabilities = [erlang_one(A, N) for N in N_values]
3.
4. plt.plot(N_values, blocking_probabilities)
5. plt.xlabel('Количество каналов (N)')
6. plt.ylabel('Вероятность блокировки (P)')
8. plt.grid(True)
9. plt.show()
10.
11. A_value = 190 # Интенсивность поступающей нагрузки
12. N_values = np.arange(1, 500, 5) # Число обслуживающих устройств
13.
14. plot_blocking_probability_N(N_values, A_value)
1.
def
plot_waiting_A(A_values,
N):
2. waiting_probabilities = [erlang_two(A, N) for A in A_values]
3. plt.plot(A_values, waiting_probabilities)
4. plt.xlabel('Интенсивность нагрузки (A)')
5. plt.ylabel('Вероятность ожидания начала обслуживания (P)')
6. plt.title(f'Зависимость вероятности ожидания начала обслуживания от интенсивности\nКоличество каналов (N) = {N}')
7. plt.grid(True)
8. plt.show()
9.
10. def plot_queue_A(A_values, N):
11. queue_lengths = [queue(A, N) for A in A_values]
12. plt.plot(A_values, queue_lengths, color='orange')
13. plt.xlabel('Интенсивность нагрузки (A)')
14. plt.ylabel('Средняя длина очереди (n)')
16. plt.grid(True)
17. plt.show()
18.
19. n_value = 190*2 # Число обслуживающих устройств
20. A_values = np.linspace(0.1, 500, 50) # Интенсивность нагрузки
21.
22. plot_waiting_A(A_values, n_value)
23.
24. n_value = 190*2 # Число обслуживающих устройств
25. A_values = np.linspace(0.1, 350, 100) # Интенсивность нагрузки
26.
27. plot_queue_A(A_values, n_value)
1.
def
plot_waiting_N(A,
N_values):
2. waiting_probabilities = [erlang_two(A, N) for N in N_values]
3. plt.plot(N_values, waiting_probabilities)
4. plt.xlabel('Количество каналов (N)')
5. plt.ylabel('Вероятность ожидания начала обслуживания (P)')
6. plt.title(f'Зависимость вероятности ожидания начала обслуживания от количества обслуживающих устройств\nИнтенсивность нагрузки (A) = {A}')
7. plt.grid(True)
8. plt.show()
9.
10.
11. def plot_queue_N(A, N_values):
12. queue_lengths = [queue(A, N) for N in N_values]
13. plt.plot(N_values, queue_lengths, color='orange')
14. plt.xlabel('Количество каналов (N)')
15. plt.ylabel('Средняя длина очереди (n)')
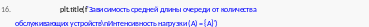
17. plt.grid(True)
18. plt.show()
19.
20. A_value = 190 # Интенсивность поступающей нагрузки
21. N_values = np.arange(1, 300, 200) # Число обслуживающих устройств
22.
23. plot_waiting_N(A_value, N_values)
24.
25. A_value = 190 # Интенсивность поступающей нагрузки
26. N_values = np.arange(200, 500, 5) # Число обслуживающих устройств
27.
28. plot_queue_N(A_value, N_values)
Графики зависимостей:
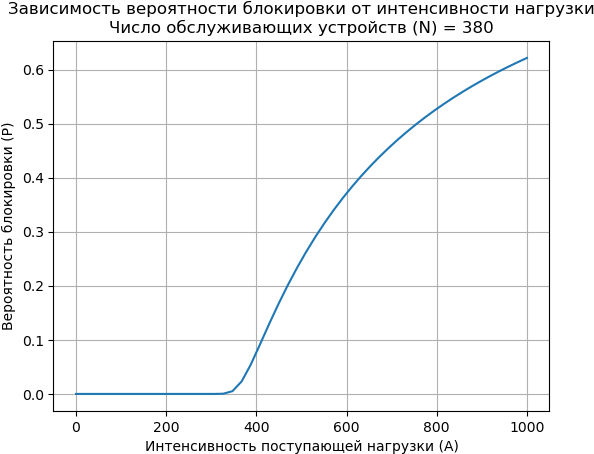
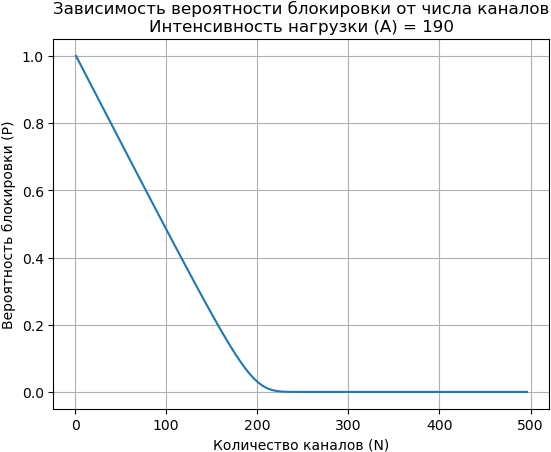
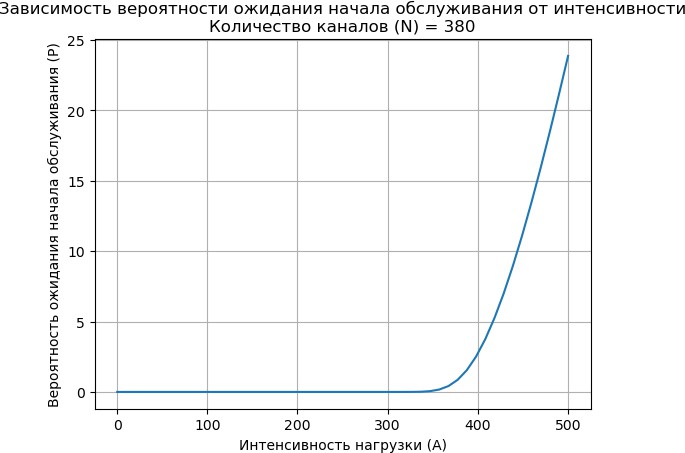
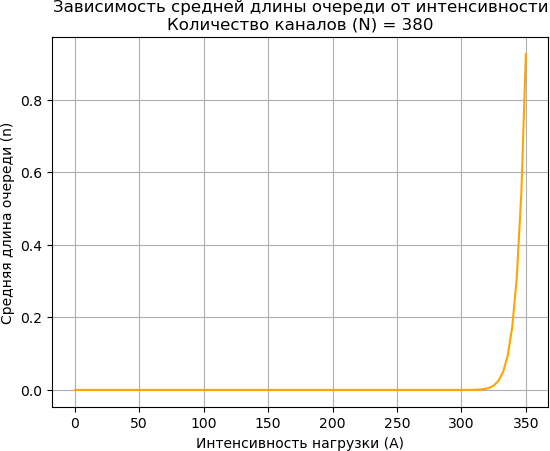
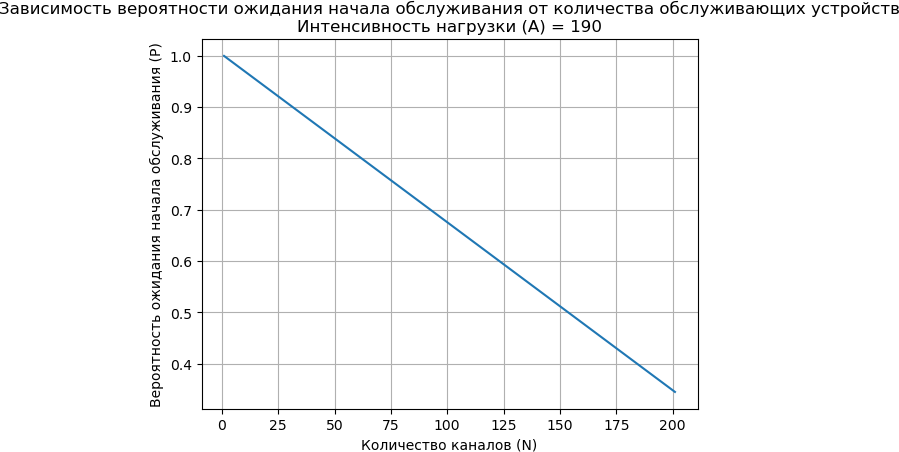
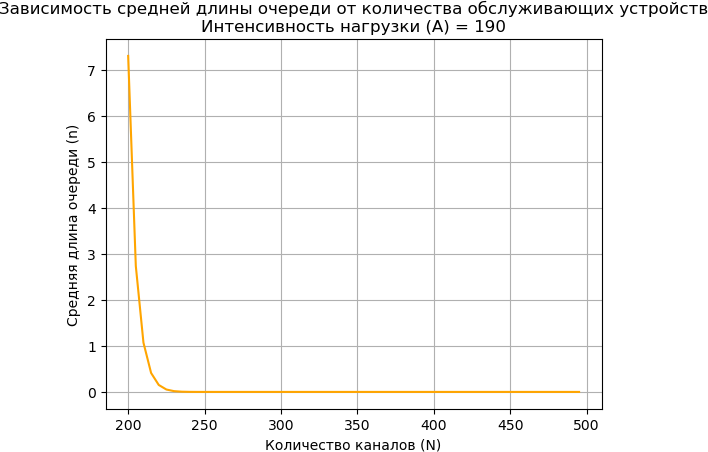
Вывод:
В ходе данной работы были изучены первая и вторая формулы Эрланга.
Были написаны реализации данных формул на языке программирования Python.
При помощи графиков мы можем наглядно увидеть поведение системы при изменении различных параметров.
Формулы Эрланга имеют важное практическое применение в теории массового обслуживания, а именно для расчета вероятности блокировки (отказа) в системе с ограниченными ресурсами.
Поэтому знание данных формул является важным для разработки и оптимизации систем массового обслуживания.