МИНОБРНАУКИ РОССИИ

САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)

Кафедра ИС

ОТЧЕТ

по лабораторной работе №2 по дисциплине «ИКСиС»

Тема: Потоки заявок и освобождений. Время обслуживания.

Вариант №190

Студент гр.

Преподаватель Колбанев М.О.

Санкт-Петербург 2023

Часть 1

1. Временная диаграмма обслуживания 15 заявок CMO G/G/3.

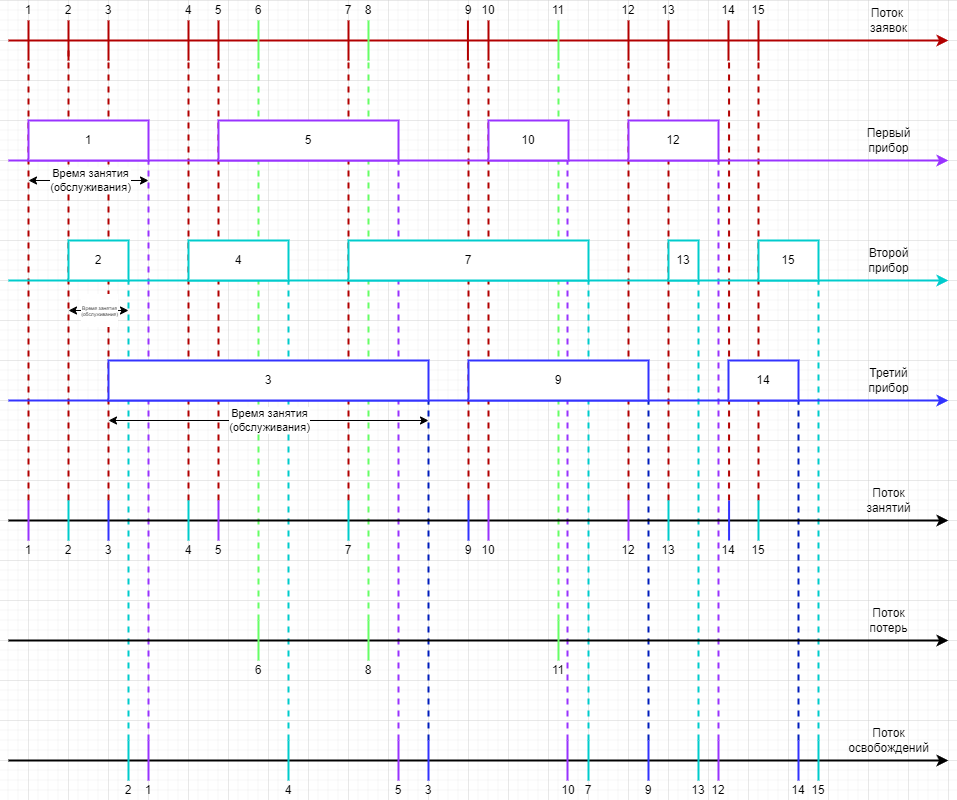
Расчёт средних времён (1 клетка = 1 минута)

Среднее время интервалов времени между поступившими заявками:

4+4+8+3+4+9+2+10+2+7+7+4+6+3

14

= 5.2 мин

Среднее время занятости первого прибора:

12+18+8+9

4

= 11.8 мин

Среднее время занятости второго прибора:

6+8+24+3+6

5

= 9.4 мин

Среднее время занятости третьего прибора:

32+18+7

3

= 19 мин

Среднее время занятости произвольного прибора:

11.8+9.4+19

3

= 13.4 мин

Среднее время между моментами занятий:

4+4+8+3+13+12+2+14+4+6+3

11

= 6.6 мин

Среднее время между моментами потерь:

11+9

2

= 15 мин

Среднее время между моментами освобождений:

2+14+11+3+14+2+7+5+2+8+2

11

= 6.4 мин

2. Временная диаграмма обслуживания 15 заявок CMO G/G/3 (потеря 10 заявок).

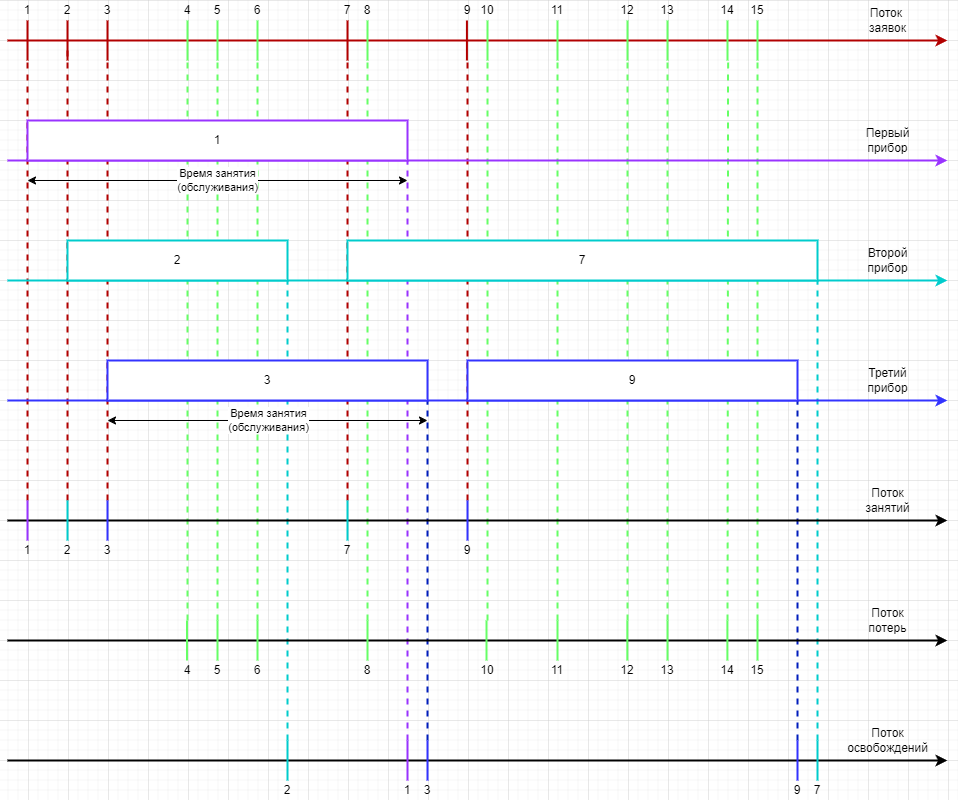
Расчёт средних времён (1 клетка = 1 минута)

Среднее время интервалов времени между поступившими заявками:

4+4+8+3+4+9+2+10+2+7+7+4+6+3

14

= 5.2 мин

Среднее время занятости первого прибора:

38

= 38 мин

1

Среднее время занятости второго прибора:

22+47

2

= 34.5 мин

Среднее время занятости третьего прибора:

32+33

2

= 32.5 мин

Среднее время занятости произвольного прибора:

38+34.5+32.5

3

= 35 мин

Среднее время между моментами занятий:

4+4+24+12

4

= 11 мин

Среднее время между моментами потерь:

3+4+11+12+7+7+4+7+3

9

= 6.4 мин

Среднее время между моментами освобождений:

12+2+37+2

4

= 13.25 мин

3. Временная диаграмма обслуживания 15 заявок CMO G/G/3/2.

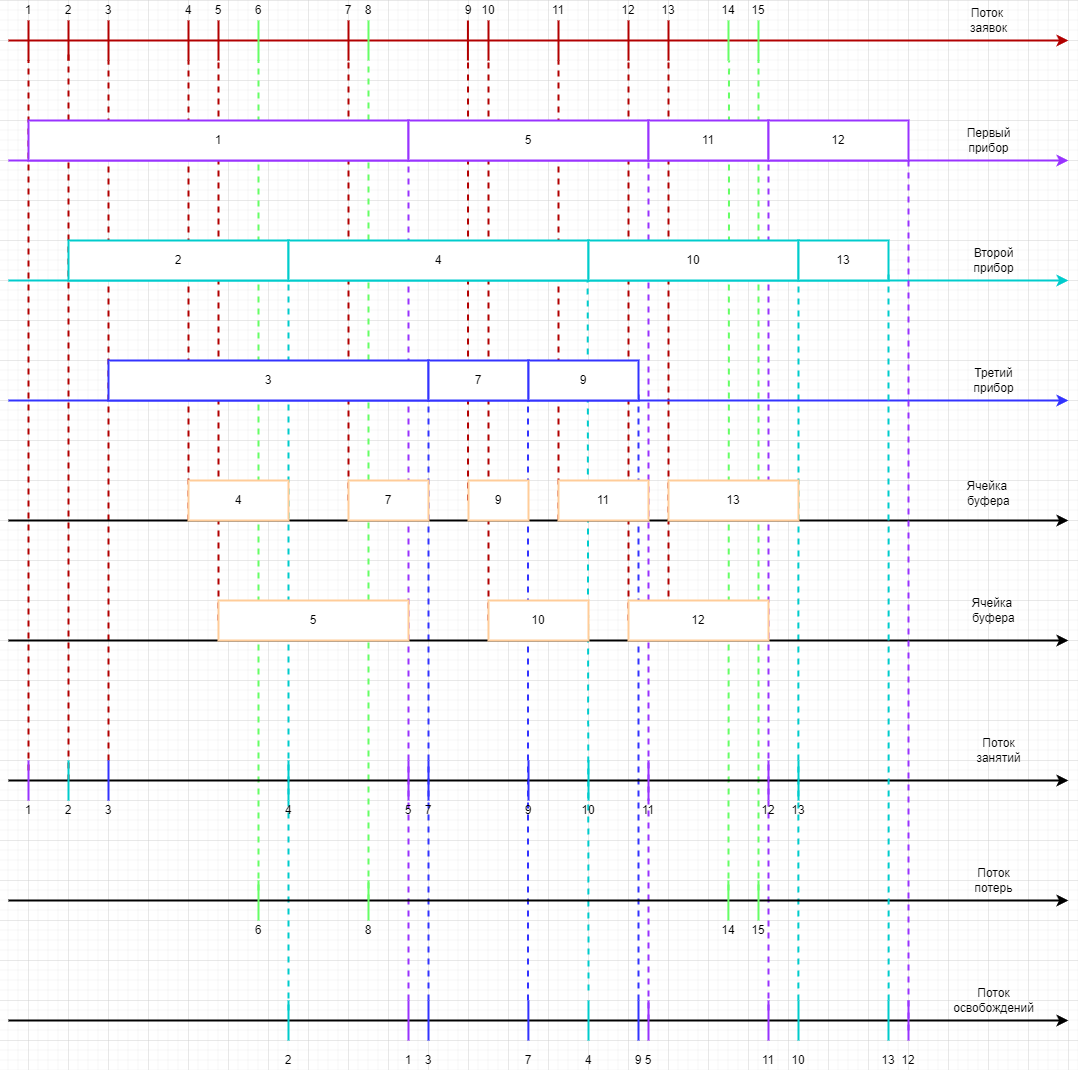
Расчёт средних времён (1 клетка = 1 минута)

Среднее время интервалов времени между поступившими заявками:

4+4+8+3+4+9+2+10+2+7+7+4+6+3

14

= 5.2 мин

Среднее время занятости первого прибора:

38+24+12+14

4

= 22 мин

Среднее время занятости второго прибора:

22+30+21+9

4

= 20.5 мин

Среднее время занятости третьего прибора:

32+10+11

3

= 17.7 мин

Среднее время занятости произвольного прибора:

22+20.5+17.7

3

= 20.1 мин

Среднее время между моментами занятий:

4+4+18+12+2+10+6+6+12+3

10

= 7.7 мин

Среднее время между моментами потерь:

11+36+3

3

= 16.7 мин

Среднее время между моментами освобождений:

12+2+12+6+5+1+12+3+9+2

10

= 6.4 мин

Среднее время пребывания заявки в очереди:

10+8+6+9+13+19+14+10

8

= 11.3 мин

Часть 2

1. Построение графиков функции и плотности трёх экспоненциальных распределений.

Параметры распределений:

1

𝜇² = 190

2

𝜇² = 380

3

𝜇² = 570

Функция распределения:

𝐵⁽𝑡⁾ = 1 − 𝑒^−𝜇𝑡

Графики функции:

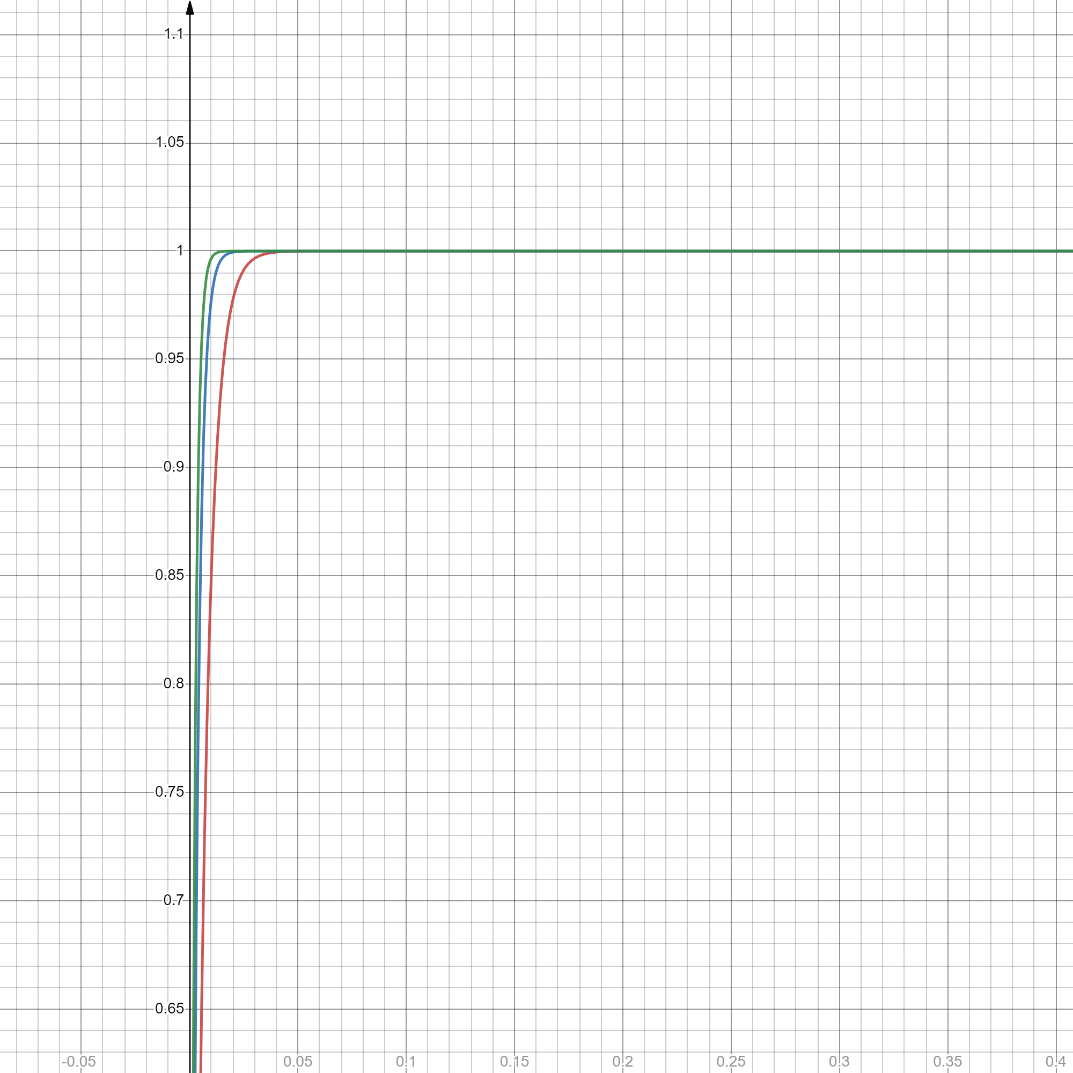
Рисунок 1 - графики функции трёх экспоненциальных распределений

Плотность экспоненциального распределения:

𝑏⁽𝑡⁾ = 𝜇𝑒^−𝜇𝑡

Графики плотности экспоненциального распределения:

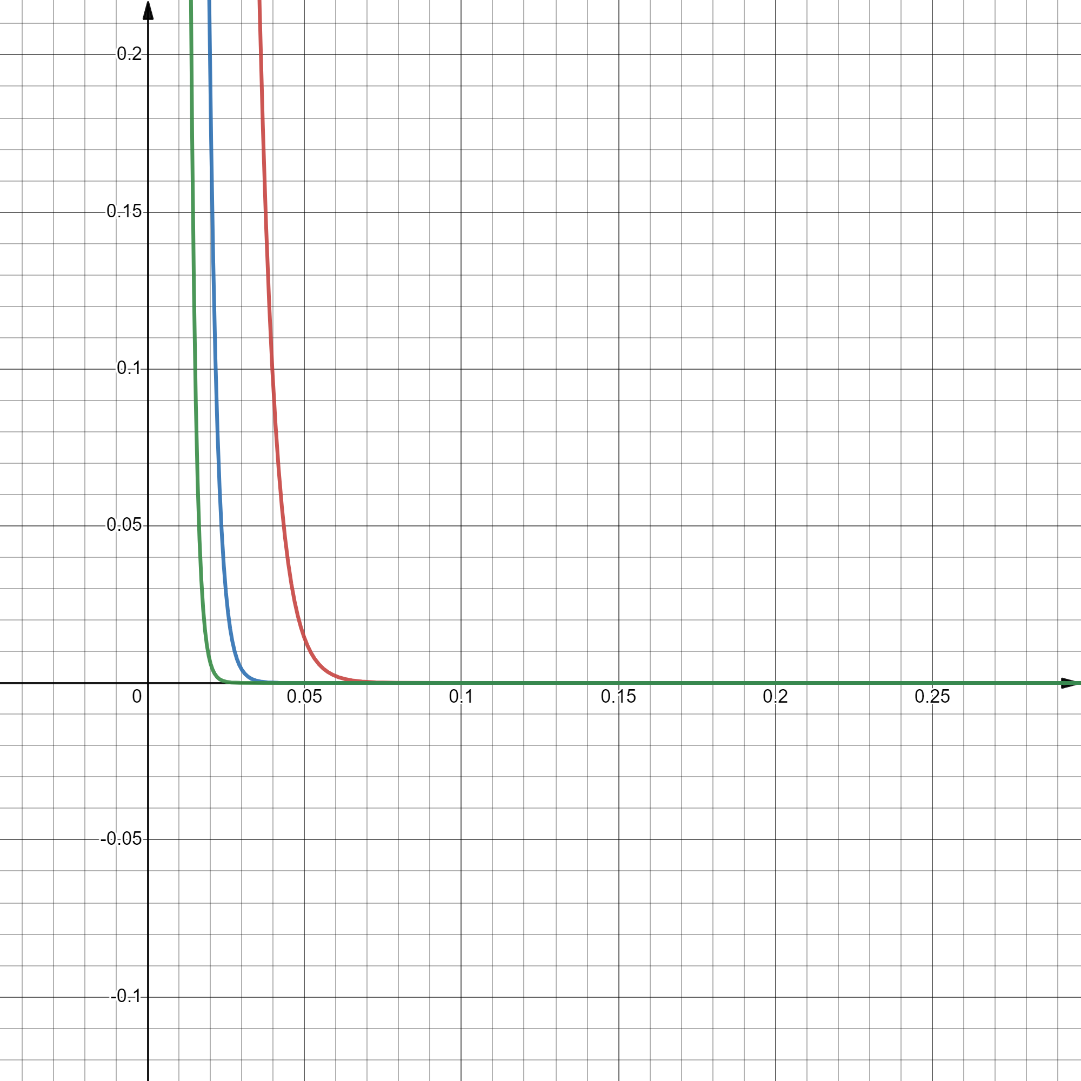
Рисунок 2 - графики плотности экспоненциального распределения

Можно сделать вывод, что чем больше μ, тем больше вероятность малых значений случайной величины.

2. Построение графиков плотности двух гиперэкспоненциальных распределений, полученных как аддитивная смесь из n = 3 экспоненциальных распределений.

Значения параметров:

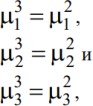
Весовые коэффициенты для первого и второго гиперэкспоненциальных распределений:

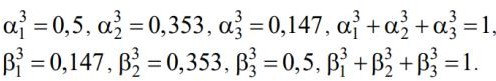
Плотность гиперэкспоненциального распределения:

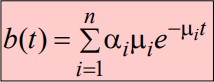
Графики плотности двух гиперэкспоненциальных распределений:

Рисунок 3 - графики плотности двух гиперэкспоненциальных распределений

3. 1

   Построение графика плотности экспоненциального распределения со значением интенсивности 𝜇⁴, вычисленной по формуле:

𝑀^[𝑋^] = ^0.5 + ^0.353 + ^0.147 ≈ 0.003818

190

380

570

1

_𝑀[𝑋] ≈ 261.917

1

График плот.ности экспоненциального распределения со значением интенсивности 𝜇⁴:

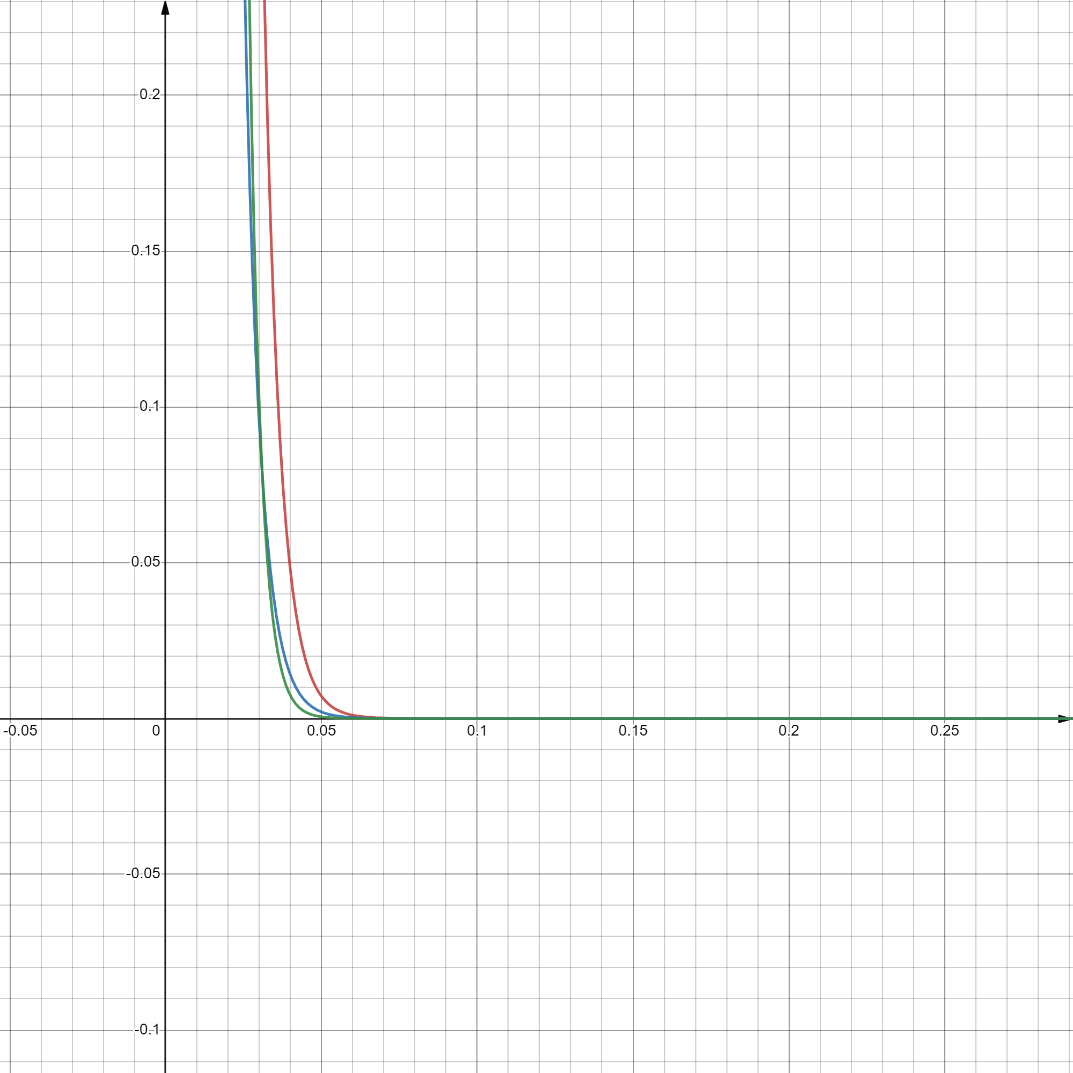
Рисунок 4 - график плотности эксп. распределения

Мм_бзрожн_оанео сса_лднелпча_ььтьрев_шывноед_иедиП_хеярлхиеибнноитляеьхншисивностей

оятнос

4. Построение графика плотности трёх нормированных эрланговских распределений, отличающихся рангом:

Вычисление интенсивностей:

𝜇⁵ = ^{2 ∙ 190} = 126.67

1 ₃

𝜇⁵ = ^126.67 = 42.22

2 ₃

𝜇⁵ = ^126.67 = 25.33

3 ₅

Плотность распределения:

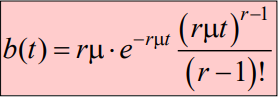
График плотности трёх нормированных эрланговских распределений:

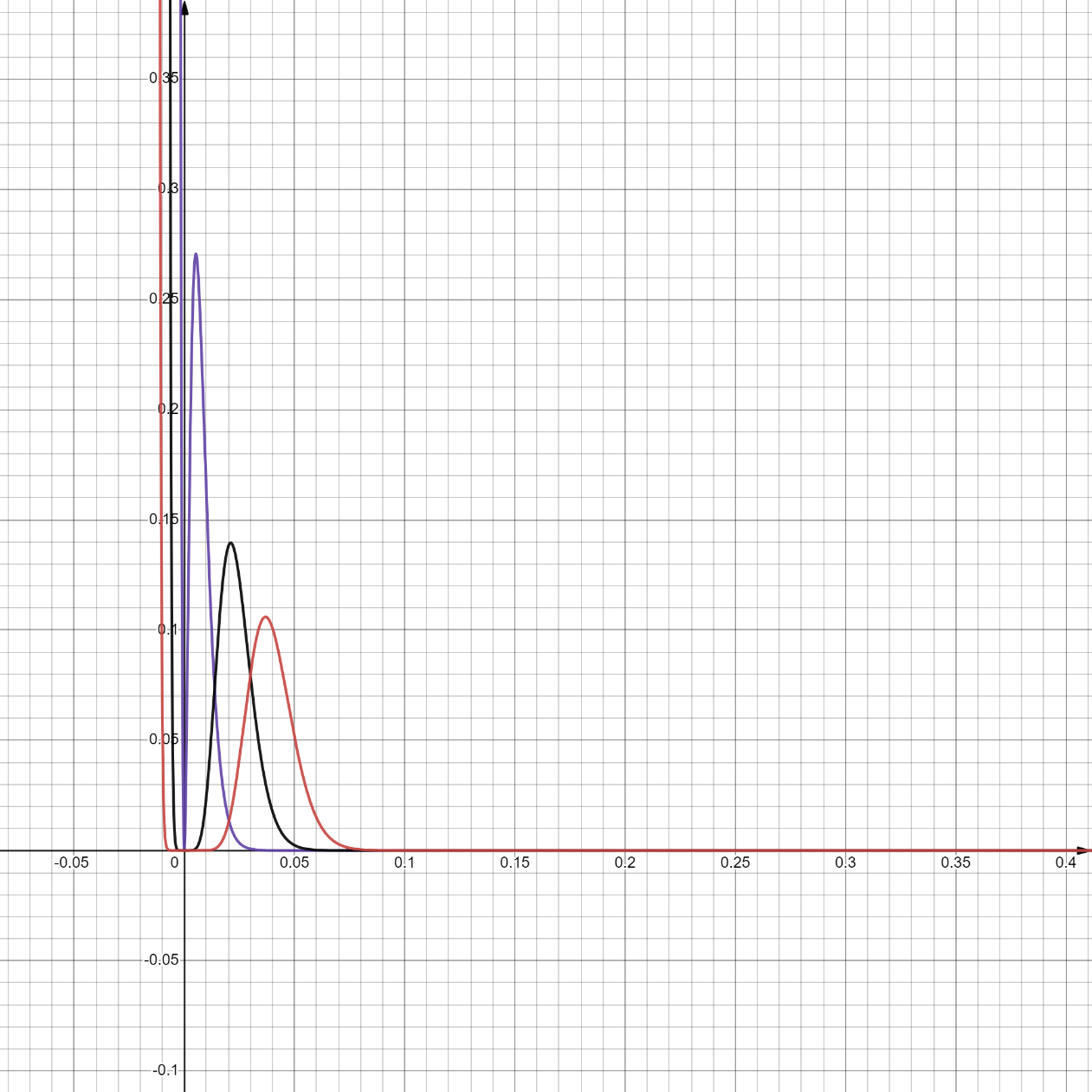
Рисунок 5 - эрланговские распределения

На рисунке выше представлены графики без первых двух множителей, чтобы можно было визуально оценить график, так как при оригинальной функции выходят слишком большие значения, что делает невозможным визуальную оценку графика и какие-либо выводы

Можно сделать вывод, что при увеличении ранга вероятность больших значений уменьшается.