Сбалансированные деревья. Авл-деревья. Алгоритм удаления существующего узла.
АВЛ-дерево — сбалансированное по высоте двоичное дерево поиска: для каждой его вершины высота её двух поддеревьев различается не более чем на 1.
Каждый узел дерева можно представить в виде структуры данных, которая содержит следующую информацию:
Сами данные, которые содержит узел
Указатель на левого потомка
Указатель на правого потомка
Указатель на родителя (не обязателен)
При этом мы еще храним показатель баланса (разность высот левого и правого поддеревьев)
Чтобы удалить узел:
У нас существуют три случая:
Узел – это лист (нет детей)
Узел имеет одного потомка и узел имеет два потомка.
Если узел лист:
Мы просто удаляем его и вызываем ребалансировку всего дерева.
Если узел имеет одного потомка – меняем их местами и удаляем узел как лист. Ребалансировка.
Если у узла два потомка – находим в правом поддереве узла минимальный элемент и перемещаем его на место удаляемого. Потом удаляем узел с помощью одной из двух вышеописанных функций. Ребалансировка.
Сбалансированные деревья. Красно-чёрные деревья. Алгоритм добавления нового узла.
Красно-черное дерево – двоичное дерево поиска, для которого введен атрибут цвета и выполняются следующие свойства:
Каждый узел или красный или черный
Корень – черный
Листья – окрашены в черный
Каждый красный узел должен иметь два дочерних черных.
Пути от узла к его листьям должны содержать одинаковое количество черных узлов.
Новый узел вставляется на место одного из листьев, окрашивается в красный цвет и к нему прикрепляются два листа. Далее происходит проверка всех свойств выше. Свойство 2 нарушится если дерево изначально было пустым, достаточно просто перекрасить в другой цвет. Свойство 3 не может быть нарушено потому что узел сразу получает черные узлы. Свойство 4 может быть нарушено если к красному узлу будет прикреплен дочерний красный, а 5 – если пути в дереве содержат разное количество черных узлов.
При нарушении пунктов происходит балансировка.
Сбалансированные деревья. Красно-чёрные деревья. Алгоритм удаления.
Удаление как в авл-дереве и проверка условий
Сбалансированные деревья. B-деревья. 2-3-4 деревья. Основные понятия.
В отличии от Красно-Чёрного дерева или АВЛ-дерева каждый узел в B-дереве может иметь несколько ключей, которые используются для поиска элемента
Для B-дерева справедливы следующие ограничения:
Каждый узел может иметь до m дочерних узлов.
Каждый нелистовой узел (кроме корневого) имеет как минимум m/2 узлов.
Корневой узел имеет минимум 2 дочерних узла, за исключением случая, когда он является и листовым.
Нелистовой узел с k дочерними узлами содержит k-1 ключ.
Глубина всех листов одинакова.
Операции:
1.Поиск ключа
2.Добавление ключа
Новый ключ при добавлении всегда помещается в листовой узел, где он должен занять своё место (сохраняя упорядоченность элементов). Но нужный узел может быть уже заполнен, поэтому необходимо уметь разбивать такой узел надвое. Примерный алгоритм выглядит следующим образом (при этом явно запретим дубликаты ключей):
Осуществить поиск ключа в дереве.
Если ключ не найден и текущий узел листовой, то добавить ключ на позицию таким образом, чтобы сохранить упорядоченность ключей в узле.
Если до добавления узел уже являлся полным, то после операции вставки нарушается ограничение на количество ключей в узле, и необходимо выполнить операцию разбиения узла на 2.
После разбиения в случае, когда родительский узел также оказывается заполненным, то операция разбиения выполняется и для родительского узла. Если таким узлом оказывается корневой, тогда разделение завершается после очередного разделения с созданием нового корневого узла с единственным ключом. Таким образом, B-дерево растёт снизу-вверх.
3-для удаления ключ из дерева достаточно провести процедуру обратную к добавлению
2–3–4 дерева (также названный деревом 2–4) являются самоуравновешивающейся структурой данных. Числа означают дерево, где каждый узел с детьми (внутренний узел) имеет или два, три, или четыре детских узла
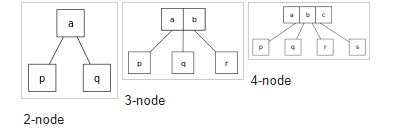
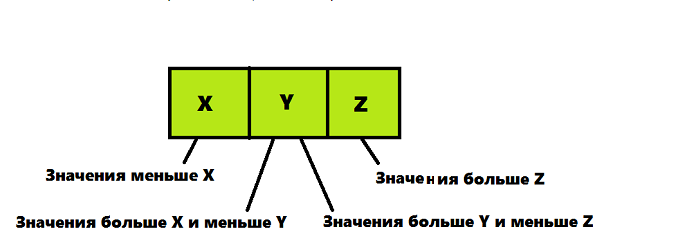
Свойства:
Каждый узел (листовой или внутренний) является 2-узлом, 3-узлом или 4-узлом и содержит один, два или три элемента данных соответственно.
Все листья находятся в одинаковая глубина (нижний уровень).
Все данные хранятся в отсортированном порядке.
Вставка
Если текущий узел -4:
Сохранить и удалить среднее значение, чтобы получить -3 узел
Разделить -3 узел на две пары узлов
Если узел корневой:
Среднее ранее удаленное значение становится новым корнем и высота дерева увеличивается на один
Если узел не корневой:
Помещаем элемент в родительский узел, поднимаемся к родительскому узлу
Находим ребенка который содержит нужное значение
Если этот дочерний элемент – лист, вставляем значение
Если
нет – спускаемся к ребенку и продолжаем
сначала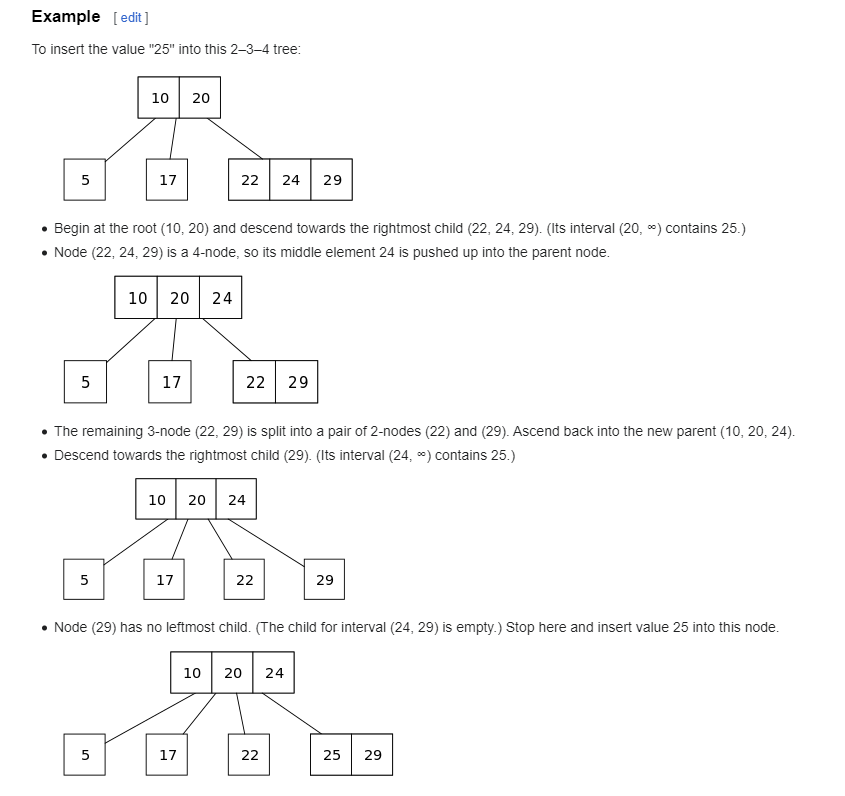
Удаление
Самая простая возможность – пометить элемент как удаленный и игнорировать его.
Затем «удаленные» элементы можно будет использовать заново при последующей вставке.
Однако недостатком этого метода является то, что дерево при таком способе не уменьшается.
1.Находим элемент который нужно удалить
Если элемент – не лист, запоминаем его место и продолжаем поиск пока не достигнем преемника элемента.
Преемник – самый большой ключ который меньше удаляемого или самый маленький ключ который больше чем тот который будет удален
Да в пизду
20. Пузырьковая сортировка (bubble)
Алгоритмы, использующие для сортировки сравнение элементов между собой, называются основанными на сравнениях.
Или сортировка простыми обменами. Принцип действий прост: обходим массив от начала до конца, попутно меняя местами неотсортированные соседние элементы. В результате первого прохода на последнее место «всплывёт» максимальный элемент. Теперь снова обходим неотсортированную часть массива (от первого элемента до предпоследнего) и меняем по пути неотсортированных соседей. Второй по величине элемент окажется на предпоследнем месте. Продолжая в том же духе, будем обходить всё уменьшающуюся неотсортированную часть массива, запихивая найденные максимумы в конец.
Сложность O(n^2)