Деревья. Дерево поиска и бинарное дерево поиска. Основные понятия.
Дерево представляет собой иерархичную структуру, где только один корневой элемент и узлы, связанные отношением потомок-родитель.
Путь до вершины — это множество переходов в дереве, от корня к необходимому узлу.
Число узлов в любом пути называется длиной пути, а максимальная длина пути из всех — высотой дерева.
Дерево – частный случай графа.
Одна из форм записи дерева – скобочная.
Дерево поиска:
оба поддерева — левое и правое — являются двоичными деревьями поиска;
у всех узлов левого поддерева произвольного узла X значения ключей данных меньше либо равны, нежели значение ключа данных самого узла X;
у всех узлов правого поддерева произвольного узла X значения ключей данных больше, нежели значение ключа данных самого узла X.
Существует три вида обхода дерева:
Прямой обход (КЛП): корень → левое поддерево → правое поддерево.
Центрированный обход (ЛКП): левое поддерево → корень → правое поддерево.
Обратный обход (ЛПК): левое поддерево → правое поддерево → корень
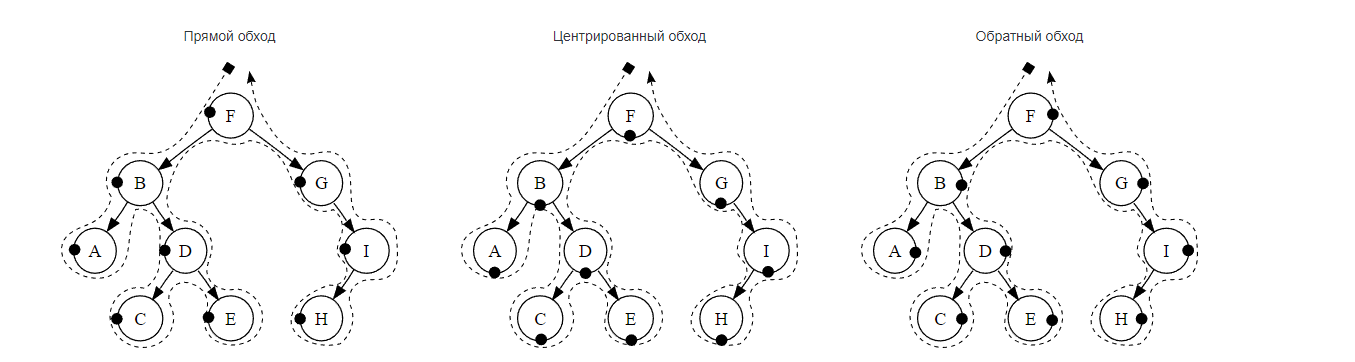
Это поиск в глубину
Существует
поиск в ширину, когда мы идем «по уровням
дерева»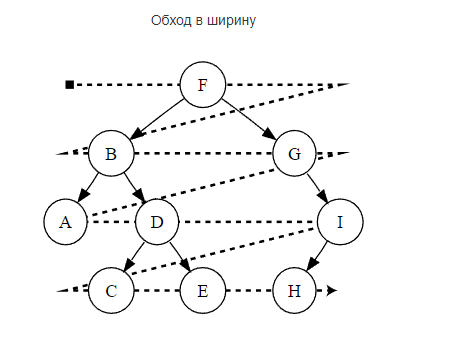
Сбалансированные деревья. Основные понятия. Малый и большой повороты дерева. Обходы дерева.
Сбалансированные деревья – сбалансированные по высоте двоичные деревья поиска.
К примеру, для каждой его вершины высота её двух поддеревьев различается не более чем на 1 (в случае АВЛ)
Поворот дерева — это операция, которая позволяет изменить структуру дерева.
Балансировкой вершины называется операция, которая в случае разницы высот левого и правого поддеревьев |высота (L)− высота (R)| = 2, изменяет связи предок-потомок в поддереве данной вершины так, чтобы восстановилось свойство дерева | высота (L)− высота (R) | ⩽ 1, иначе ничего не меняет.
Большой поворот используется в том случае, если при малом невозможно вернуть баланс и как правило состоит из двух малых поворотов.
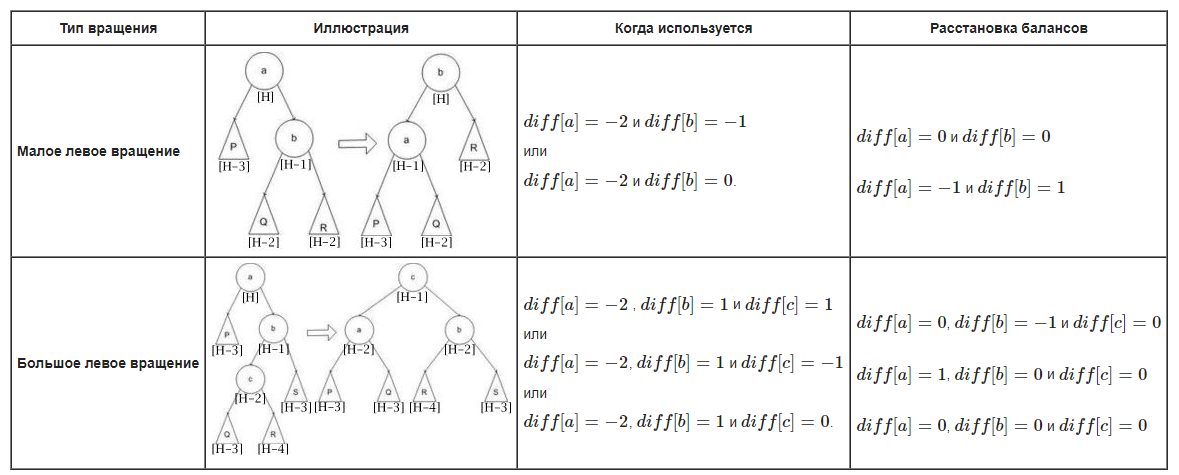
Для балансировки используется 4 типа вращений
Малое правое и большое правое вращение определяются симметрично малому левому и большому левому вращению. В каждом случае операция приводит к нужному результату, а полная высота уменьшается не более чем на 1 и не может увеличиться.
После вращения высота каждого узла пересчитывается.
Дерево можно обойти в глубину:
Прямым обходом (корень – левое – правое)
Центрированным (левое – корень – правое)
Обратным (левое - правое – корень)
И в ширину (по уровням)
Каждый узел дерева можно представить в виде структуры данных, которая содержит следующую информацию:
Сами данные, которые содержит узел
Указатель на левого потомка
Указатель на правого потомка
Указатель на родителя (не обязателен)
Высота узла – максимальная высота его потомков+1
Сбалансированные деревья. Авл-деревья. Алгоритм добавления нового узла.
АВЛ-дерево — сбалансированное по высоте двоичное дерево поиска: для каждой его вершины высота её двух поддеревьев различается не более чем на 1.
Каждый узел дерева можно представить в виде структуры данных, которая содержит следующую информацию:
Сами данные, которые содержит узел
Указатель на левого потомка
Указатель на правого потомка
Указатель на родителя (не обязателен)
При этом мы еще храним показатель баланса (разность высот левого и правого поддеревьев)
Чтобы добавить узел в АВЛ-дерево:
-Совершаем обход дерева (какие бывают?), чтобы убедиться, что узла с таким же ключом в дереве нет.
-Рекурсивно спускаемся вниз по дереву и ищем место для включения вершины (как?)
-На обратном пути пересчитываем показатель балансировки у каждого узла и +
-Проверка показателя балансировки у каждого узла
-Если нужна балансировка – применяем. (когда нужна?)
См. прошлый вопрос