Экспериментальная часть:
Исследовать в программе Matlab режим срыва слежения в замкнутой нелинейной системе по варианту.
Рисунок 74 – Собранная нелинейность
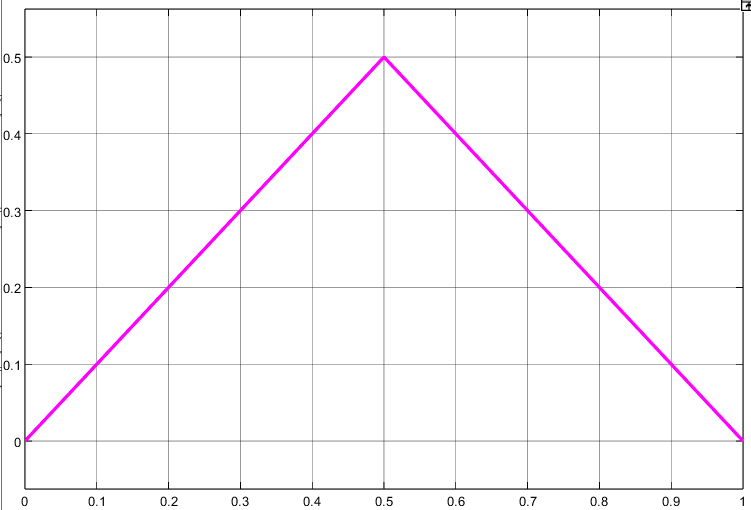
Рисунок 75 – осциллограмма при подаче на нелинейное звено
линейно возрастающего воздействия
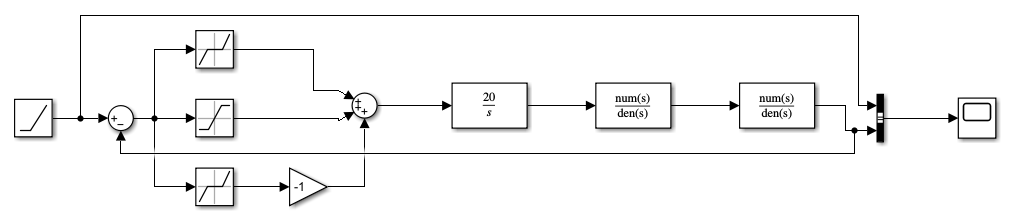
Рисунок 76 – Полная замкнутая система с нелинейной частью. Линейное воздействие
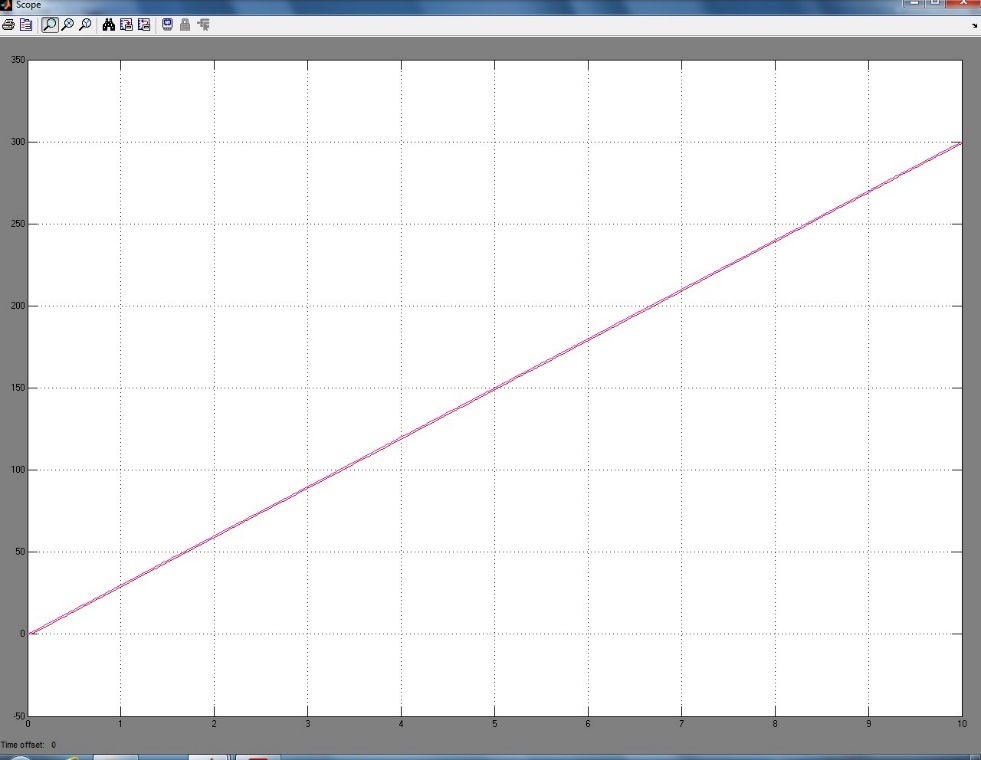
Рисунок 77 – График без срыва
Рисунок 78 – Срыв происходит при значении Slope = 30.02 (Граничная (Последняя амплитуда 30.01))
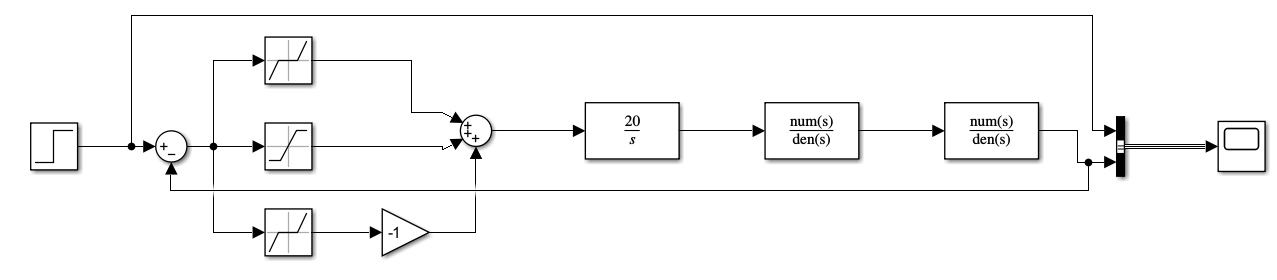
Рисунок 79 – Полная замкнутая система с нелинейной частью. Ступенчатое воздействие
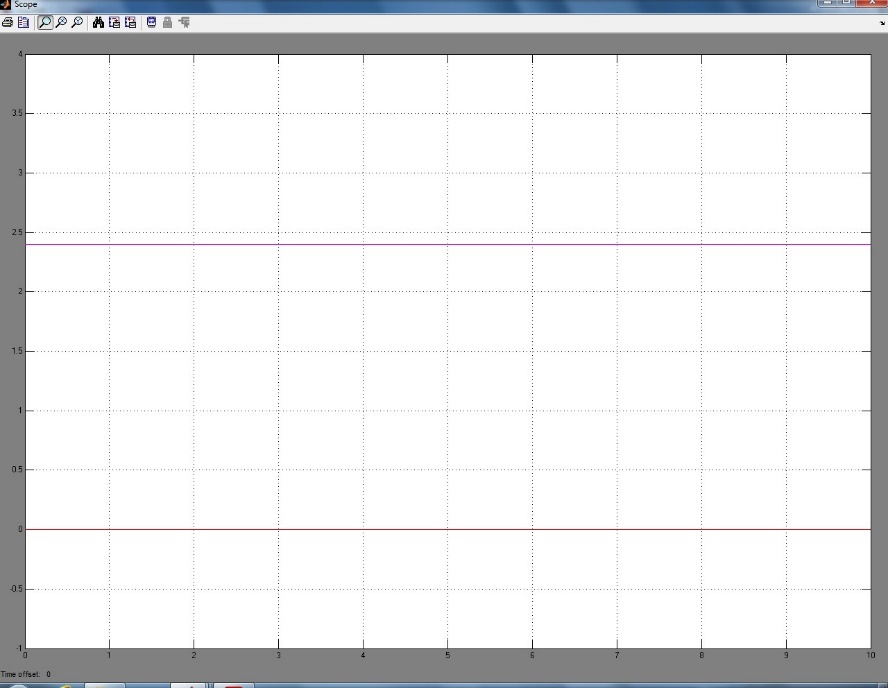
Рисунок 80 – Срыв наблюдения (Граничная амплитуда 2.39)
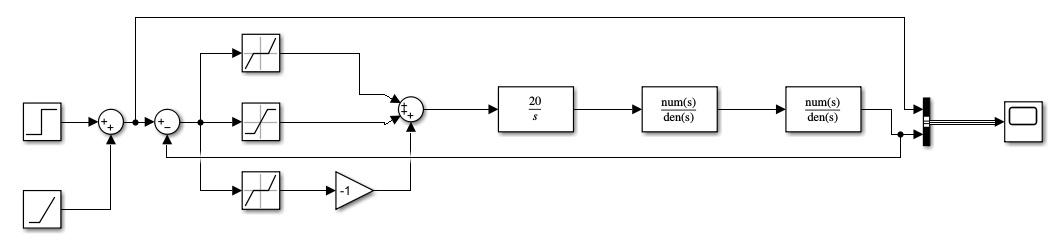
Рисунок 81 – Полная замкнутая система с нелинейной частью. Суммарная
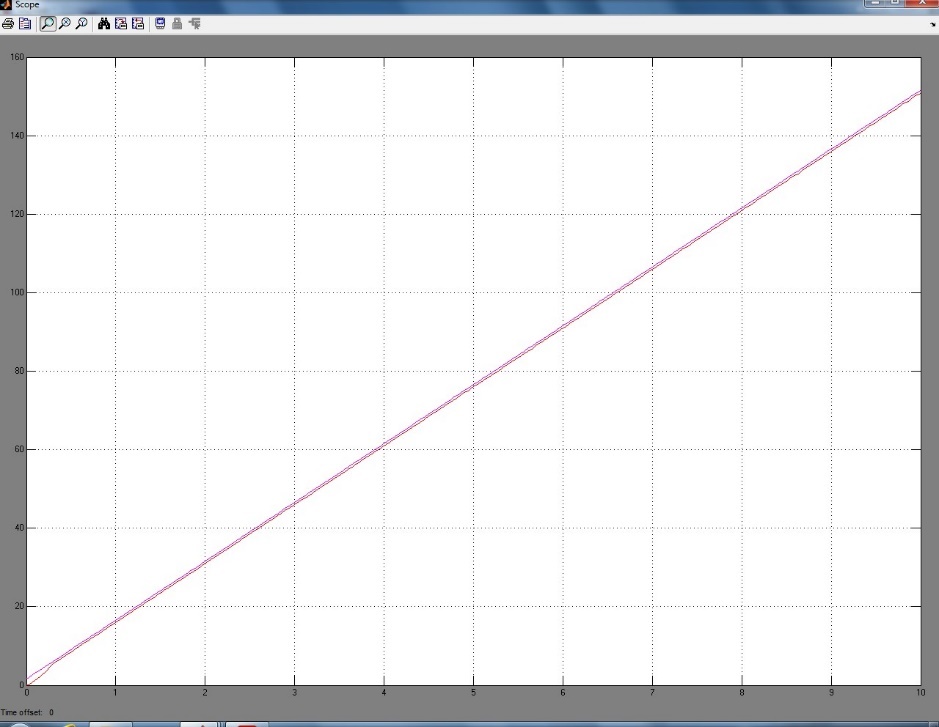
Рисунок 82 – Суммарное воздействие (Slope = 15 и Final Value = 1.58)
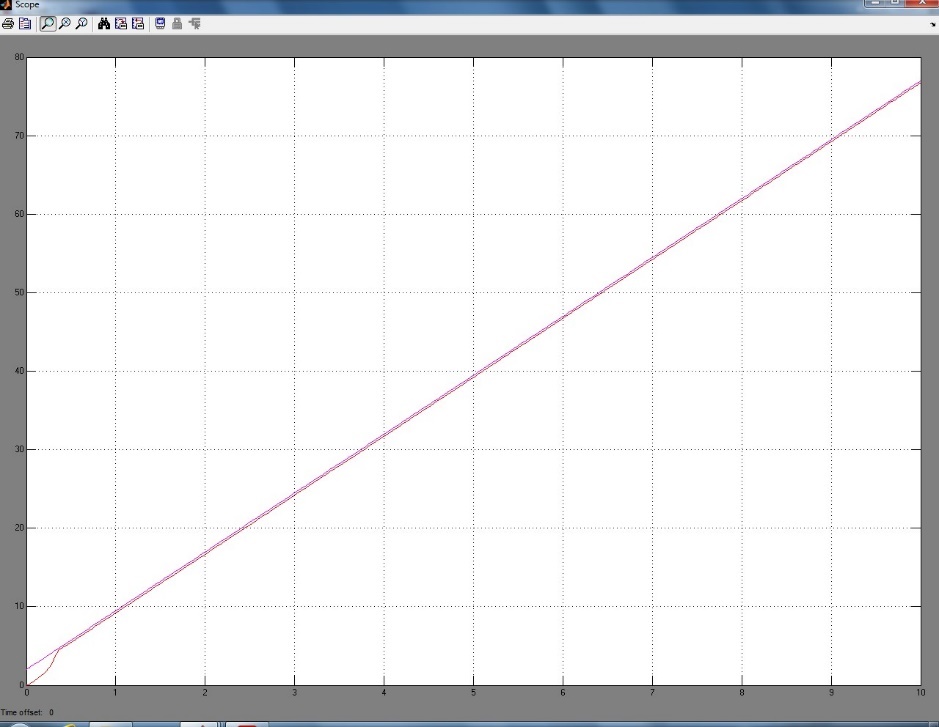
Рисунок 83 – Срыв наблюдения (Slope = 7.5 и Final Value = 1.99)
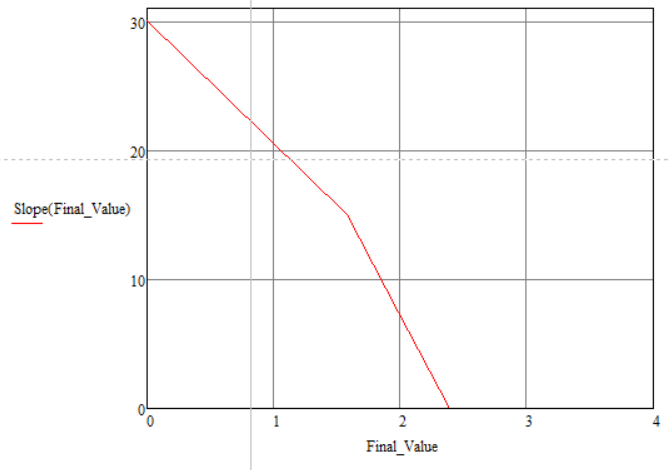
Рисунок 84 – Рабочая область
Вывод:
В ходе выполнения лабораторной работы были исследованы реакции цепей с включёнными нелинейностями на линейно нарастающее и ступенчатое входные воздействия. По результатам экспериментов можно сделать вывод, что максимальная амплитуда воздействия, при котором в системе не происходит срыва слежения в случае линейно нарастающего воздействия в разы больше, чем в случае ступенчатого. Так, для ступеньки величина амплитуды "срыва" составляет 1, в то время как для линии 6,5. Однако стоит отметить, что даже без срыва, реакция цепи на линейно нарастающее воздействие отклоняется всё дальше и дальше от самого воздействия. При комбинированном входном сигнале достигается некий оптимум, при котором на граничной амплитуде имеется некоторое отклонение в начале воздействия и почти полное совпадение графиков ближе к концу.
Преобразование исследуемой системы в импульсную путём добавления импульсного п-образного элемента; построение частотных и импульсных характеристик для полученной системы
Исходные данные:
Таблица 8 – Исходные данные для расчёта
W(s) |
W(w) |
|
|
|
|
|
|
|
|
|
|
Проведём разложение выражения желаемой системы на более простые дроби.
При формировании импульсной системы передаточная характеристика строится из образующего элемента, функция которого описывается следующим образом:
После добавления этого элемента непрерывная часть передаточной функции будет описываться следующим образом:
Произведём разложение по формуле:
Решив систему уравнений, получим:
Запишем формулу желаемого звена после разложения:
Выполним
-преобразование
полученной последовательности и добавим
импульсный элемент:
Подставим в формулу значения Tд, вычислим и приведем к виду (TW+1):
Приведём получившуюся функцию к общему знаменателю и для числителя найдём постоянную времени Т, полученные корни используем для дальнейшего преобразования (формула выше).
Таким образом получаем следующие данные для нижней границы:
Корни:
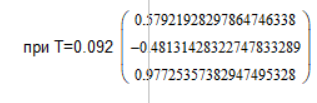
Промежуточное значение будет:
Корни:
Полученное выражение:
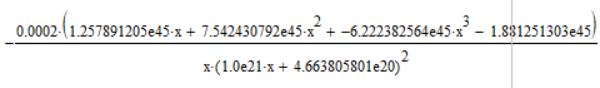
Верхняя граница:
Корни:
Полученное выражение:
