Экспериментальная часть

Построить полученное желаемое звено и снять реакции на ступенчатое и линейно нарастающее воздействие, а также ошибки.

Соберём схемы:

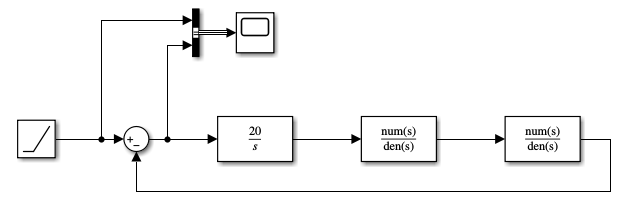
Рисунок 64 – Схема скорректированной цепи с линейно нарастающим входным воздействием

Рисунок 65 – Схема скорректированной цепи со ступенчатым входным воздействием

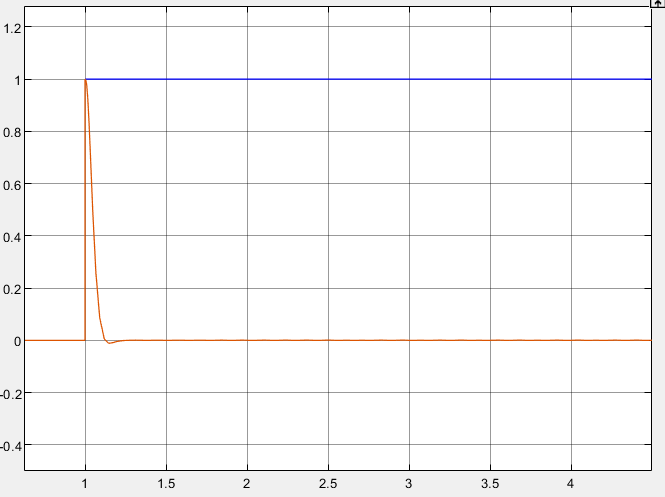
Рисунок 66 – График воздействие и ошибки в скорректированной цепи "Ступенчатое воздействие"

Рисунок 67 – График воздействия и ошибки в скорректированной цепи "Линейно нарастающее воздействие"

Определим значение установившейся ошибки:

Хмв1:

Хмв2:

Ср. кв. значение флуктуационной составляющей ошибки:

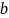По полученному выражению определяем коэффициенты и , благодаря которым в дальнейшем будет доступно вычисление установившейся ошибки

Наивысшая степень коэффициента данного уравнения n=2, для которого справедливо следующее выражение:

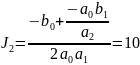
Подставляя значения, получаем:

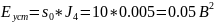
Вывод:

В ходе выполнения лабораторного практикума были получены, при помощи построения неизменной части, желаемое и звено коррекции. Были построены ЛАЧХ, ЛФЧХ и АФЧХ всех частей. Так же в ходе выполнения были получены графики ступенчатого и линейно нарастающего воздействия и ошибки в скорректированной цепи. По полученным данным, можно сделать вывод, что время установления ошибки, в отличие от нескорректированной цепи, становится намного меньше.

5. Расчёт параметров и характеристик желаемого звена с введённой нелинейностью; исследование срыва слежения при различных видах воздействий Задание:

Рассчитать и построить эквивалентные нормированные коэффициенты передачи для нелинейного звена НЗ1 с S-образной треугольной характеристикой и нелинейного звена НЗ2 – звена с линейной зоной и насыщением, проверить методом гармонического баланса, используя логарифмическую плоскость, возможно ли возникновение автоколебаний в нелинейной системе по варианту, а если при параметрах желаемой системы автоколебания невозможны, то указать минимально возможный коэффициент усиления скорректированной системы или Кна, при котором они возможны, иследовать в программе Matlab режим срыва слежения в замкнутой нелинейной системе по варианту, получить S-образную статическую характеристику нелинейной части, собрать на лабораторной установке полную замкнутую систему с нелинейной частью, подавая на вход системы линейно возрастающее и ступенчатое воздействия, а также их сумму, определить границы рабочей зоны системы;

Предварительный расчёт Начальные данные

Таблица 6 – Исходные данные

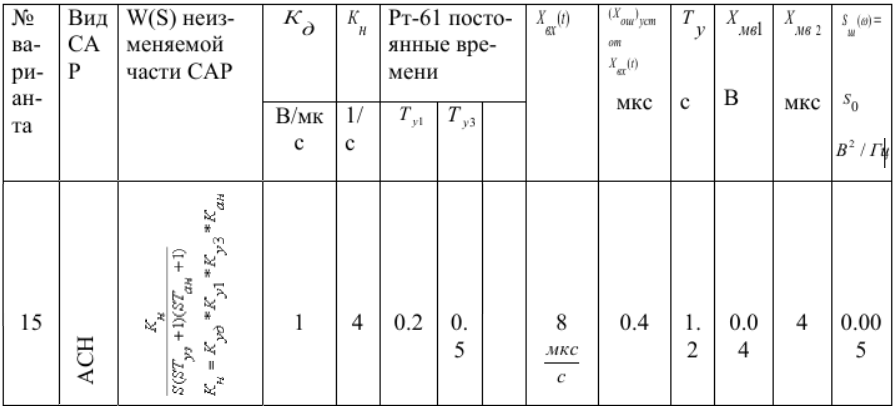
Расчётная часть

Рассчитаем эквивалентные нормированные коэффициенты по формулам:

Звено Нз1:

Звено Нз2:

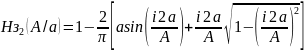
Звено Нз3:

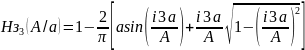
Найдем общее звено системы Нз. Суммируем:

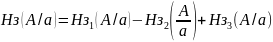
Найдем:

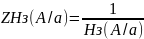
Найдем в дБ:

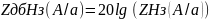
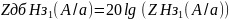
Получаем данные:

Таблица 7 – Исходные данные

A/a	1	2	3	4	5	6	7	8	9	10
I(A/a)НЗ1	1	0.22	0.05	0.03	0.01	0.01	0.01	0	0	0
ZНЗ1	1	4.54	20	33.3	100	100	100	∞	∞	∞
20lg(ZНЗ1)	1	13.14	26.02	30.44	40	4	40	∞	∞	∞
I(A/a)НЗ2	1	0.61	0.42	0.32	0.25	0.21	0.18	0.16	0.14	0.13
ZНЗ2	1	1.04	2.4	3.15	3.95	4.73	5.52	6.3	7.08	7.87
20lg(ZНЗ2)	0	4.31	7.61	10.04	11.34	13.51	14.83	15.99	17.01	17.97
I(A/a)НЗ3	0	0.39	0.58	0.68	0.74	0.78	0.81	0.84	0.85	0.87
ZНЗ3	∞	2.56	2.72	1.47	1.35	1.28	1.23	1.19	1.17	1.14
20lg(ZНЗ3)	∞	8.16	4.71	3.34	2.6	2.14	1.79	1.51	1.31	1.13
I(A/a)НЗ4	0	0	0.21	0.39	0.5	0.58	0.64	0.68	0.7	0.74
ZНЗ4	∞	∞	4.76	2.56	2	1.72	1.56	1.47	1.4	1.35
20lg(ZНЗ4)	∞	∞	13.55	8.16	6.02	4.71	3.86	3.34	2.92	2.6

Построим графики:

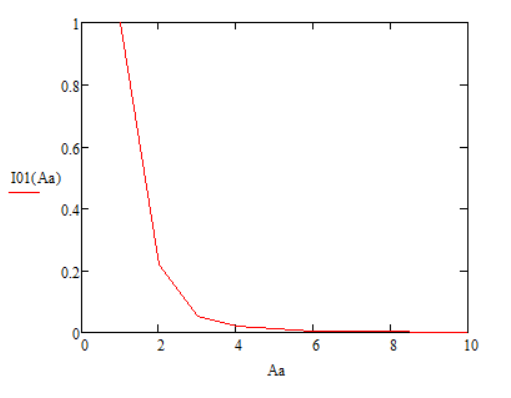
Рисунок 68 – График I₀(A/a) для Нз

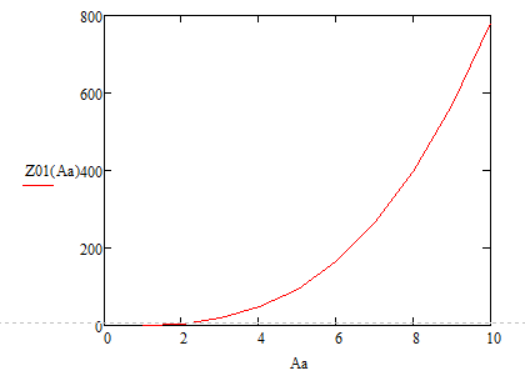
Рисунок 69 – График Z₀(A/a) для Нз

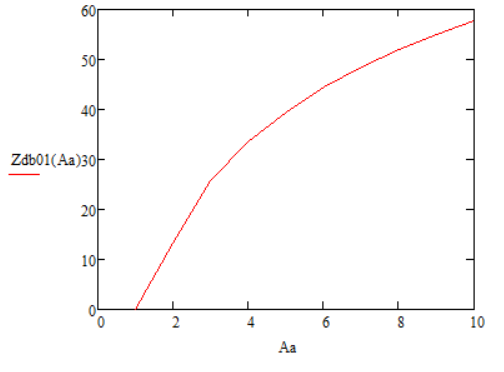
Рисунок 70 – График 20log(Z₀(A/a)) для Нз

Рисунок 71 – График I₀(A/a) для Нз1

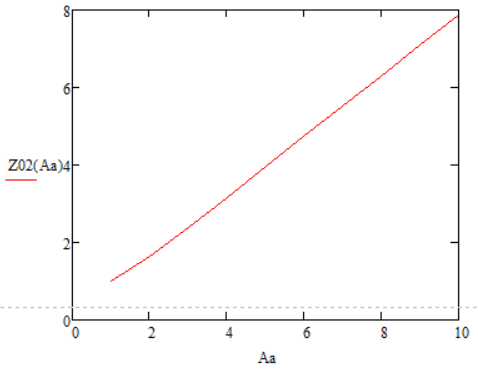
Рисунок 72 – График Z₀(A/a) для Нз1

Рисунок 73 – График 20log(Z₀(A/a)) для Нз1