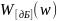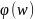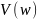МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

СВЯЗИ И ИНФОРМАТИКИ

(МТУСИ)

Факультет "Радио и телевидение"

Кафедра "Радиотехнические системы "

Курсовая работа

по дисциплине: "Радиоавтоматика"

на тему: "Расчёт и моделирование системы АСД"

Исполнитель:

студент ____________________________________ Цой Дон Чер

Проверила: ________________________________ О. Н. Минаева

СОДЕРЖАНИЕ

1. Теоретические сведения об АСД 3

2. Разложение цепи на динамические звенья и расчёт параметров с ООС и без 5

3. Нахождение зависимости времени установления переходного процесса от коэффициента усиления цепи 36

4. Расчёт и построение желаемого звена и звена коррекции; их характеристик 46

5. Расчёт параметров и характеристик желаемого звена с введённой нелинейностью; исследование срыва слежения при различных видах воздействий 53

Задание: 53

Начальные данные 53

Расчётная часть 54

6. Преобразование исследуемой системы в импульсную путём добавления импульсного П-образного элемента; построение частотных и импульсных характеристик для полученной системы 63

СПИСОК ЛИТЕРАТУРЫ 73

Исходные данные системы

1. Теоретические сведения об асд

Дальномер РЛС предназначен для измерения дальности до выбранной цели. Принцип работы дальномера базируется на измерении сдвига между зондирующими импульсами, следуемыми через интервал времени Т, и импульсами, отраженными от цели. Отраженные от цели импульсы искажены шумами, поэтому непосредственное измерение дальности по времени задержки связано с большими ошибками. Для повышения точности измерения в дальномере формируются следящие импульсы, временное положение которых относительно зондирующих импульсов оказывается пропорциональным дальности до цели и незначительно зависит от шумов.

— воздействие, описывающее поступающие на вход АСД отраженные импульсы в виде функции времени.

n(t) — случайная помеха. Ухудшает качество работы дальномера.

Т — период измерения пары следящих импульсов.

F(e) — звено с характеристикой, соответствующей временному дискриминатору. Вид этой характеристики зависит от ОСШ и длительности следящих импульсов.

Э — экстраполятор. Фиксирует напряжение на выходе временного дискриминатора, сбрасывает напряжение до нуля перед приходом следующей пачки следящих импульсов.

ФНЧ — фильтр нижних частот. Фильтрует шум и пропускает низкочастотную составляющую пары импульсов. Для повышения точности в ФНЧ дальномера включают два интегратора, в такой системе ошибка измерения дальности равна нулю при изменении расстояния до цели по линейному закону.

Uф — напряжение на выходе фильтра.

ВМ — временной модулятор. Зондирующим импульсом, задержанным на время, пропорциональным сигналу с выхода ФНЧ, запускается генератор импульсов, формирующий два следящих импульса. Образует замкнутый контур, в котором рассогласование сводится к минимальному значению, определяющему ошибку измерения дальности.

2. Разложение цепи на динамические звенья и расчёт параметров с оос и без Расчётная часть

В качестве неизменяемой части рассчитываемой системы задана следующая передаточная функция. Представим её как совокупность динамических звеньев:

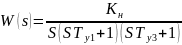
Это выражение можно разбить на два звена:

1. Инерционное звено 1

2. Инерционное звено 2

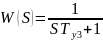
3. Интегрирующее звено

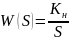
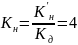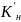Заметим, что , где и 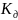– табличные числа.

Инерционное звено 1

Найдём передаточную функцию звена.

Сделаем преобразование Фурье и вычислим действительную и мнимую части:

Из данного выражения выразим АЧХ:

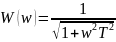
Из данного выражения выразим ФЧХ:

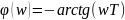
Переведём АЧХ в логарифмический вид.

В данном случае, K = 1.

Вывод формул для построения годографа звена:

Из преобразования Фурье найдём действительную и мнимую части.

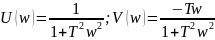
Вычислим реакцию звена на единичный скачок.

Характеристика будет иметь вид. См таблица 3.1

Вычислим реакцию на линейно возрастающее значение:

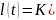
Таблица 1 – Инерционное звено 1 без ООС

	0,1	1	10 (1/T)	100	1000
	1	0.995	0.707	0.1	0.01
	0	0	-3	-20	-40
	0.01	-0.1	-0.785	-1.471	-1.561
	1	0.99	0.5	0.009	0
	-0,1	-0,099	-0,05	-0,001	0

Проведём расчёты параметров для инерционного звена с ООС.

В данном случае, передаточная характеристика звена будет выглядеть следующим образом:

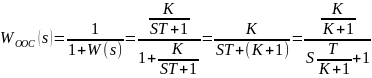
Следовательно,

Где:

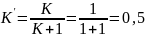
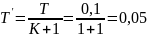
Дальнейшие расчёты проводятся аналогично звену без ООС.

Таблица 2 – Инерционное звено 1 с ООС

	0,1	1	10	1/T(20)	100	1000
	0,449	0,456	0,354	0,108	0,011	0,0011
	-6,029	-6,821	-9,031	-19,29	-39,08	-59,08
	-2,57	-24,2	-45	-77,47	-88,727	-89,9
	0,49	0,416	0,25	0,024	0,0002	0
	-0,022	-0,187	-0,25	-0,106	-0,011	-0,0011

Рисунок 1 – ЛАЧХ инерционного звена 1

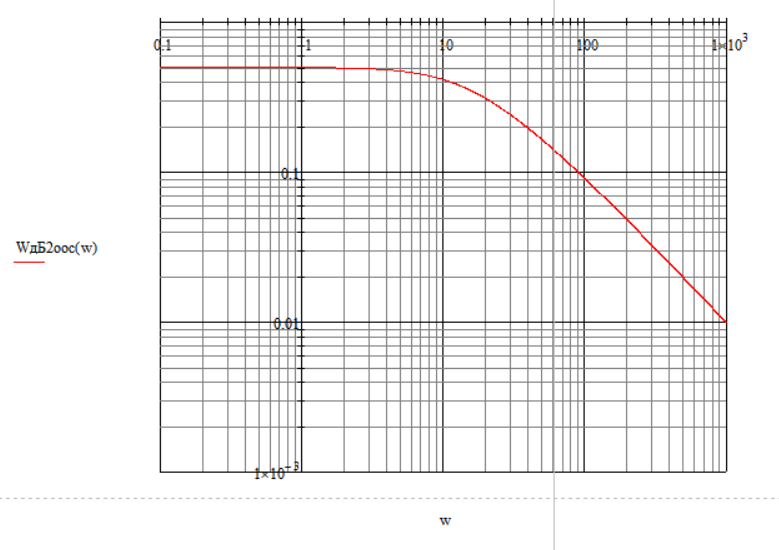
Рисунок 2 – ЛАЧХ инерционного звена 1 с ООС

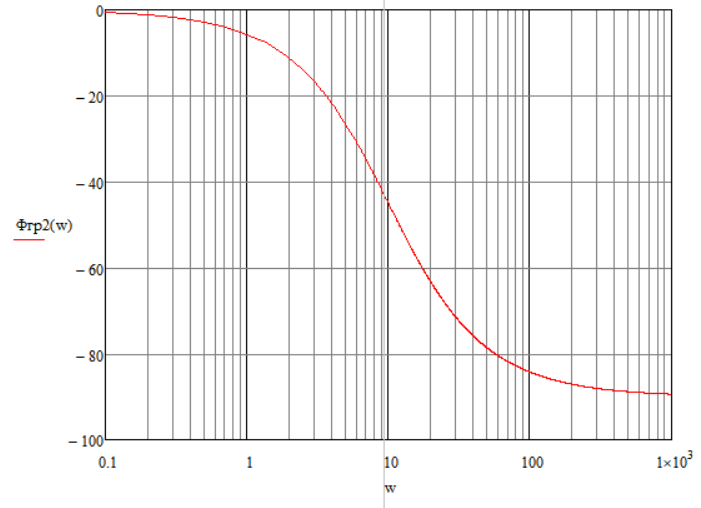
Рисунок 3 – ЛФЧХ инерционного звена 1

Рисунок 4 – ЛФЧХ инерционного звена 1 с ООС

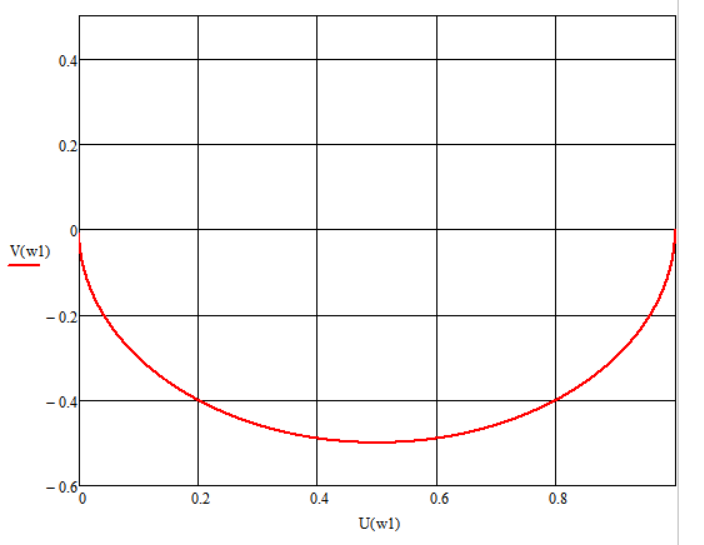
Рисунок 5 – Годограф инерционного звена 1

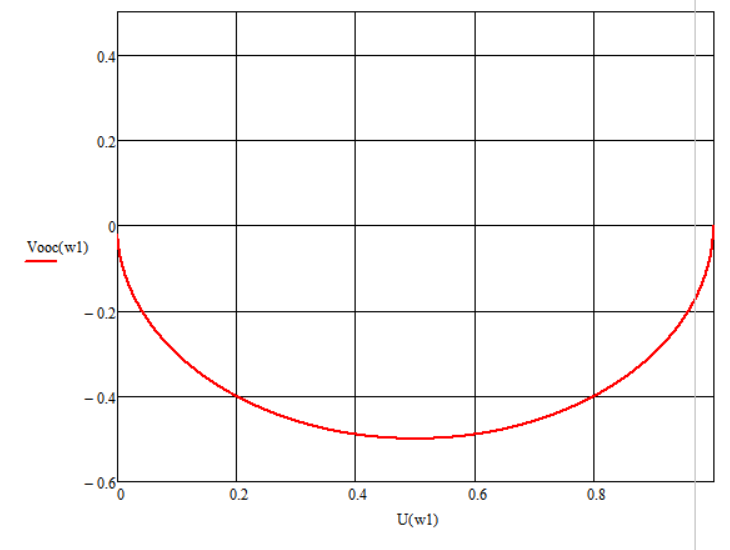
Рисунок 6 – Годограф инерционного звена 1 с ООС

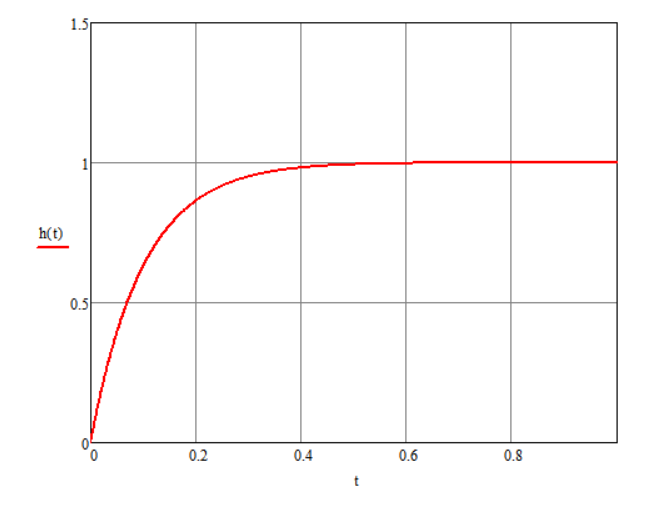
Рисунок 7 – Реакция на единичный импульс звена 1

Рисунок 8 – Реакция на единичный импульс звена 1 с ООС

Рисунок 9 – Реакция на линейно возрастающее воздействие звена 1

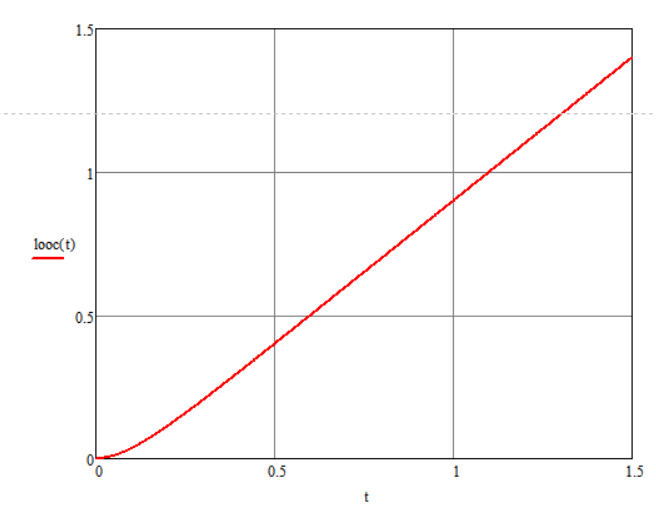
Рисунок 10 – Реакция на линейно возрастающее воздействие звена 1 с ООС