ЛР1

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ЭПУ

отчет

по лабораторной работе №1

по дисциплине «Цифровая схемотехника»

Тема: «Исследование простейших комбинаторных логических схем»

Студент гр.
Преподаватель

Санкт-Петербург

2024

Цель - ознакомиться с лабораторным стендом, предназначенным для выполнения лабораторных работ по дисциплине «Цифровая Схемотехника», исследовать таблицы истинности стандартных логических элементов и теорему Де Моргана, получить навыки сборки и изучения схем сумматора и дешифратора, также снять таблицу истинности неизвестной комбинаторной схемы, по которой восстановить ее алгебраическую формулу и электрическую схему.

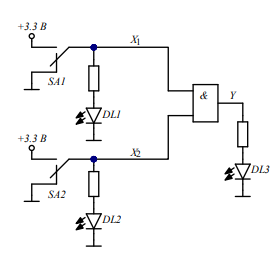
Рис. 1. Схема для исследования ЛЭ 2И

Табл. 1. Таблица истинности ЛЭ 2И

X2	X1	Y
0	0	0
0	1	0
1	0	0
1	1	1

Таблица истинности соответствует выражению алгебры логики для ЛЭ 2И, имеющему вид:

Y = X₁ * X₂

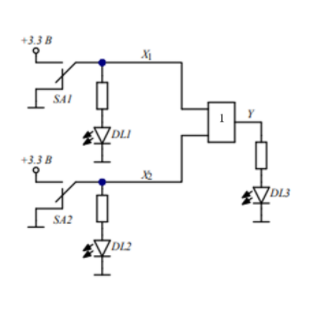
Рис. 2. Схема для исследования ЛЭ 2ИЛИ

Табл. 2. Таблица истинности ЛЭ 2ИЛИ

X2	X1	Y
0	0	0
0	1	1
1	0	1
1	1	1

Таблица истинности соответствует выражению алгебры логики для ЛЭ 2И, имеющему вид:

Y = X₁ + X₂

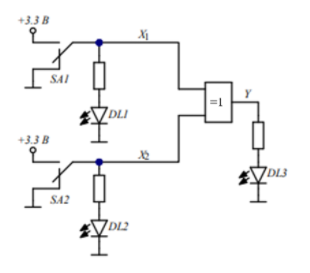
Рис. 3. Схема для исследования ЛЭ Исключающее ИЛИ

Табл. 3. Таблица истинности ЛЭ Исключающее ИЛИ

X2	X1	Y
0	0	0
0	1	1
1	0	1
1	1	0

Таблица истинности соответствует выражению алгебры логики для ЛЭ 2И, имеющему вид:

Табл. 4. Таблица истинности схемы с тремя входами

X3	X2	X1	Y
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	1
1	1	1	0

На основании полученной таблицы истинности можно записать выражение алгебры логики для исследованной схемы. Выполнив преобразования, его можно упростить и привести к виду:

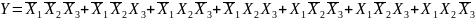
Отталкиваясь от полученного выражения и табл. 4, можно прийти к выводу, что исследованная схема имеет следующий вид:

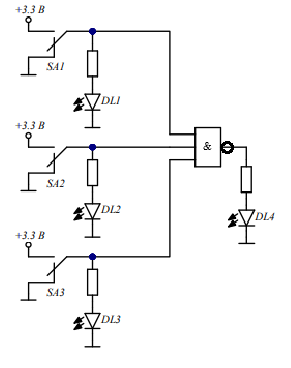
Рис. 4. Схема электрическая принципиальная, составленная на основе результатов исследований неизвестного функционального узла.

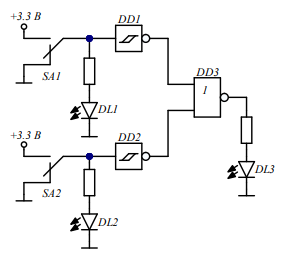
Рис. 5. Схема для исследования теоремы Де Моргана (реализация ЛЭ 2И на ЛЭ 2ИЛИ-НЕ)

Табл. 5. Таблица истинности ЛЭ 2И, реализованном с использованием ЛЭ 2ИЛИ-НЕ

X2	X1	Y
0	0	1
0	1	0
1	0	0
1	1	0

Таблица истинности соответствует теореме Де Моргана, которая для исследованной схемы имеет вид:

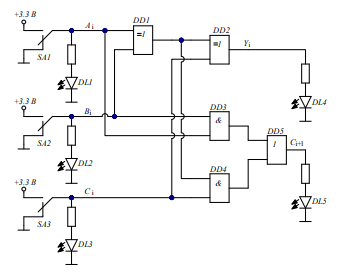
Рис. 6. Схема двоичного сумматора

Табл. 6. Таблица истинности схемы сумматора

Выражение	Результат (двоичн.)	Результат (десятичн.)
0+0+0	00	0
0+0+1	01	1
0+1+0	01	1
0+1+1	10	2
1+0+0	01	1
1+0+1	10	2
1+1+0	10	2
1+1+1	11	3

Результат исследований схемы сумматора соответствует схеме и принципу ее действия.

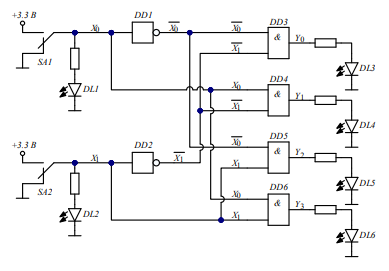
Рис. 7. Схема дешифратора «2 в 4»

Табл. 7. Таблица схемы дешифратора «2 в 4»

X1	X0	Y3	Y2	Y1	Y0
0	0	0	0	0	1
0	1	0	0	1	0
1	0	0	1	0	0
1	1	1	0	0	0

Результат исследований схемы дешифратора соответствует схеме и принципу ее действия.

Вывод: в данной лабораторной работе были изучены различные логические элементы, такие как И, ИЛИ, ИСКЛ ИЛИ. Были составлены таблицы истинности и алгебраические выражения для данных элементов. Так же были рассмотрены и изучены комбинаторные узлы дешифратор 2 в 4 и сумматор.

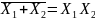Дополнительно было определено, что неизвестной схемой является схема 3И-НЕ. Была подтверждена теорема Де Моргана: таблица 5 и следующее после него алгебраическое выражение является противоположностью таблице 1 и его алг. выражению ( ).