
- •Введение
- •Структурная схема цифровой системы связи
- •Исходные данные для расчёта системы цифровой связи Вариант 9
- •Раздел 1. Источник сообщения
- •Раздел 2. Аналогово-цифровой преобразователь
- •Раздел 3. Кодер
- •2) Структурная схема кодера:
- •3) Определение последовательности кодовых символов:
- •4) Решётчатая диаграмма свёрточного кодера от момента времени до момента времени и путь, соответствующий полученному кодовому символу:
- •Раздел 4. Формирователь модулирующих сигналов
- •1) Сигнальное созвездие для квадратурной фазовой модуляции кам – 16:
- •2) Аналитические выражения реализаций c(t) случайного процесса c(t), реализации I(t) и q(t) на выходе блока фмс:
- •Раздел 5. Модулятор Подраздел 5.1. Сглаживающий формирующий фильтр
- •1) Структурная схема модулятора в составе цсс (рис. 18):
- •2) Сигнал со «спектром приподнятого косинуса» (импульса Найквиста) (рис. 19) и его спектральной плотности (рис. 20) для значений коэффициента сглаживания :
- •3) Графики спектральных плотностей и (рис. 21) сигналов и , где импульс Найквиста при коэффициенте сглаживания ; импульс со спектральной плотностью :
- •4) Импульсы и (рис. 22):
- •5) Cлучайные процессы и :
- •Подраздел 5.2. Блоки перемножителей, инвертор, сумматор
- •1) Корреляционные функций и случайных сигналов и на выходах перемножителей, где случайная фаза с равномерной плотностью вероятности на интервале
- •2) Корреляционная функция (рис. 25) и спектральная плотность мощности сигнала на выходе сумматора для кфм – 4 (рис. 26).
- •Раздел 6. Непрерывный канал
- •Раздел 7. Демодулятор
- •Раздел 8. Декодер
- •Заключение
- •Список литературы
- •Приложение а
4) Решётчатая диаграмма свёрточного кодера от момента времени до момента времени и путь, соответствующий полученному кодовому символу:
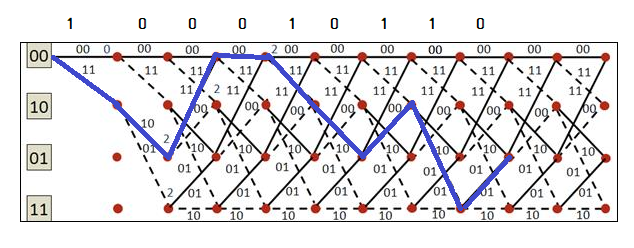
Рисунок 8 — Решётчатая диаграмма свёрточного кодера
Раздел 4. Формирователь модулирующих сигналов
Изменить графики во всём разделе
1) Сигнальное созвездие для квадратурной фазовой модуляции кам – 16:
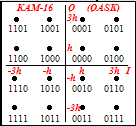
Рисунок 9 — Сигнальное созвездие для КАМ - 16
2) Аналитические выражения реализаций c(t) случайного процесса c(t), реализации I(t) и q(t) на выходе блока фмс:
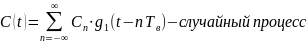
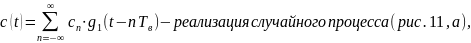
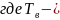 длительность
двоичного символа
длительность
двоичного символа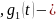 прямоугольный
импульс длительностью
прямоугольный
импульс длительностью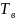 ,
,
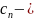 численный
коэффициент, являющийся реализацией
случайной величины
численный
коэффициент, являющийся реализацией
случайной величины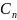 на
n-интервале
.
на
n-интервале
.
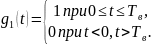
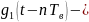 прямоугольный
импульс такой же формы, как
прямоугольный
импульс такой же формы, как
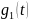 (рис. 11, б), но сдвинутый вправо относительно
импульса
на величину
(рис. 11, б), но сдвинутый вправо относительно
импульса
на величину
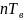 ,
если
,
если
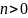 ,
или влево, если
,
или влево, если
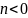 .
.
На
выходах блока ФМС для КФМ-4 (рис. 10) также
появляются сигналы
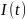 и
и
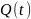 (рис. 11, в, г), представленные в виде
формул:
(рис. 11, в, г), представленные в виде
формул:
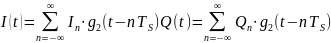
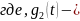 прямоугольный
импульс длительностью
прямоугольный
импульс длительностью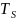 ,
,
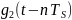 аналлогично
аналлогично
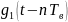 ,
,
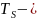 длительность
модулирующих сигналов
длительность
модулирующих сигналов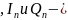 независимые
случайные величины, которые согласно
сигнальному созвездию принимают четыре
дискретных значения –3h,
–h,
+h
,+3h
с вероятностями:
независимые
случайные величины, которые согласно
сигнальному созвездию принимают четыре
дискретных значения –3h,
–h,
+h
,+3h
с вероятностями:
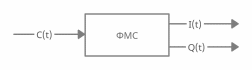
Рисунок 10 — Формирователь модулирующих символов
Определим
длительность двоичного символа
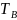 на выходе кодера:
на выходе кодера:
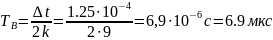
и длительность модулирующих сигналов:
для
QASK:
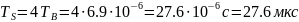
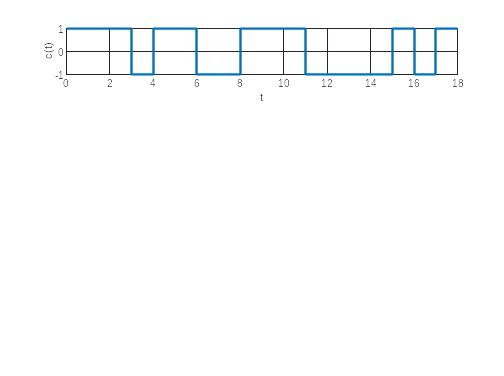
Рисунок
11 — а) реализация
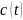 случайного процесса
случайного процесса
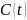 ,
формируемого с выхода блока свёрточного
кодера; б) осциллограмма прямоугольного
импульса
,
формируемого с выхода блока свёрточного
кодера; б) осциллограмма прямоугольного
импульса
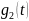 длительностью
длительностью
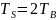 ;
в) реализация
;
в) реализация
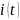 случайного процесса
случайного процесса
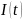 на выходе блока ФМС; г) реализация
на выходе блока ФМС; г) реализация
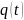 случайного процесса
случайного процесса
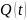 на выходе блока ФМС
на выходе блока ФМС
3)
Корреляционная функция
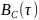 (рис. 12) и спектральная плотность мощности
(рис. 12) и спектральная плотность мощности
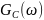 (рис. 13) входного случайного процесса
(сигнала на входе ФМС):
(рис. 13) входного случайного процесса
(сигнала на входе ФМС):
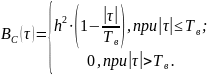
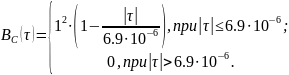
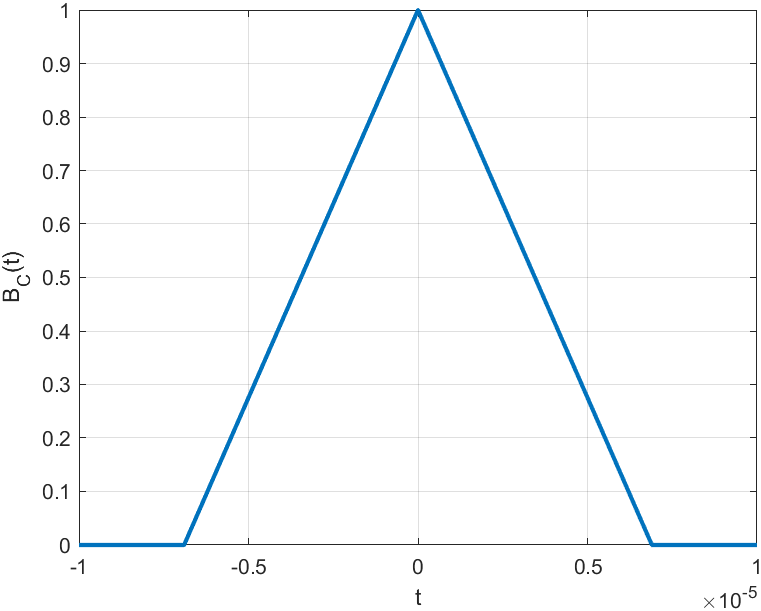
Рисунок 12 — График корреляционной функция случайного процесса
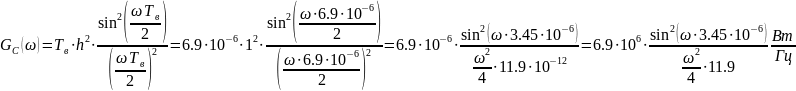
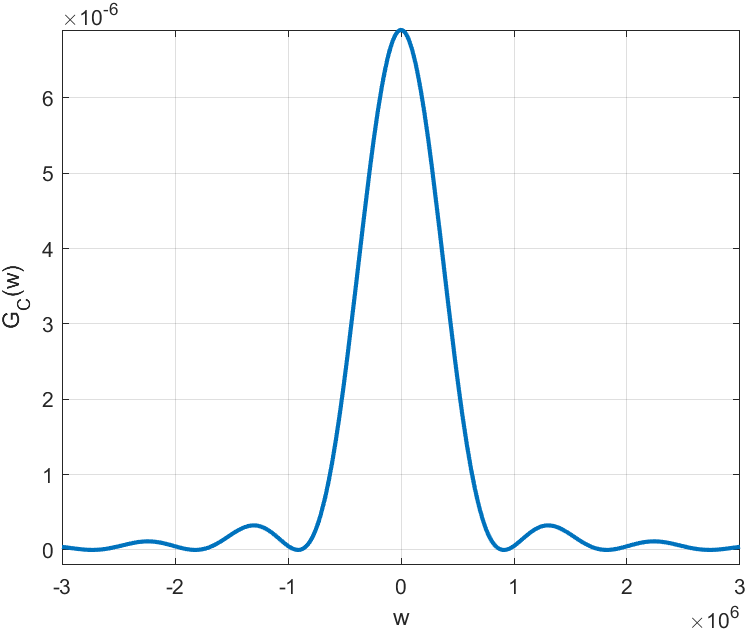
Рисунок
13 — Спектральная плотность мощности
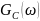 случайного процесса
случайного процесса
3)
Корреляционные функции
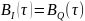 (рис. 14) и спектральные плотности мощности
(рис. 14) и спектральные плотности мощности
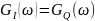 (рис. 15):
(рис. 15):
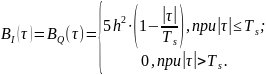
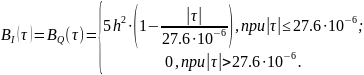
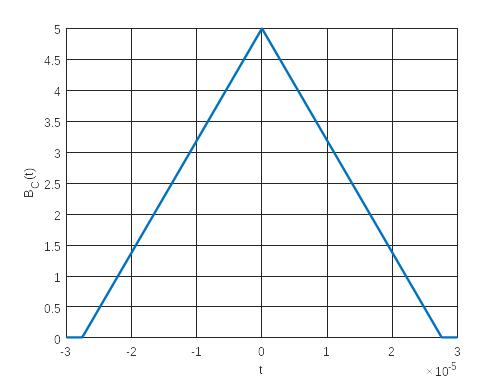
Рисунок 14 — График корреляционных функций

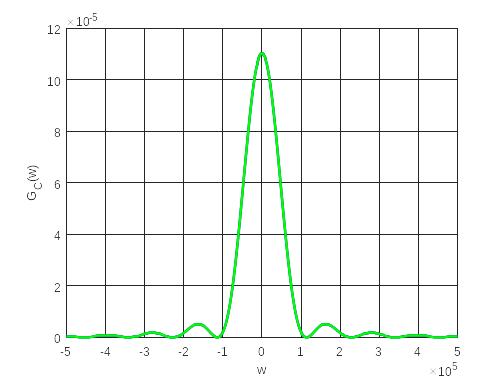
Рисунок
15 — Спектральные плотности мощности
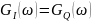
4)
Сравнение корреляционных функций
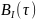 ,
,
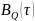 ,
(рис. 16) и спектральных плотностей
мощности
,
(рис. 16) и спектральных плотностей
мощности
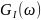 ,
,
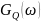 ,
синфазного
и квадратурного
сигналов (сигналов на выходе ФМС) (рис.
17):
,
синфазного
и квадратурного
сигналов (сигналов на выходе ФМС) (рис.
17):
Отличие
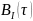 от корреляционной функции
от корреляционной функции
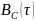 проявляется в том, что вместо множителя
проявляется в том, что вместо множителя
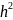 используется множитель
используется множитель
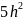 и вместо параметра
используется параметр
и вместо параметра
используется параметр
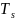
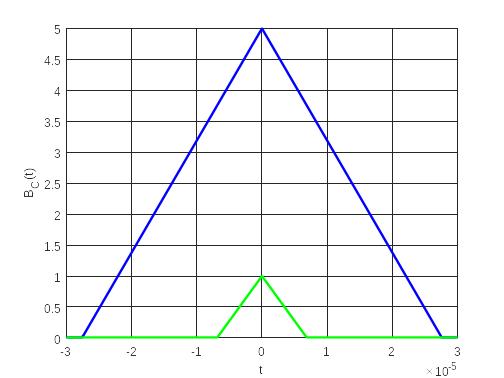
Рисунок
16 — Графики корреляционных функций
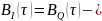 сплошлая
линия
сплошлая
линия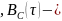 пунктирная
линия
пунктирная
линия
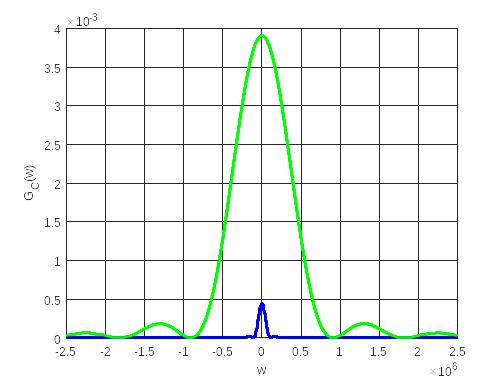
Рисунок
17 — Спектральные плотности мощности
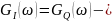 сплошлая
линия
сплошлая
линия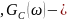 пунктирная
линия
пунктирная
линия
6) Анализ графиков (рис. 16, 17).
Корреляционные
функции сигналов на выходе блока ФМС в
4 раза шире, чем корреляционные функции
на входе. Это объясняется увеличением
длительности интервала
 .
.
Для
того, чтобы объяснить сужение спектра,
обратимся к преобразованию Фурье.
Возьмём
функцию, зависящую от величины
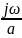 и выразим через прямое преобразование
Фурье:
и выразим через прямое преобразование
Фурье:
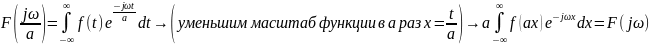
Уменьшив
масштаб, получаем функцию зависящую от
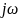 .
Таким образом, подставляя вместо
.
Таким образом, подставляя вместо
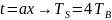 ,
получаем сужение частотного спектра в
4 раза.
,
получаем сужение частотного спектра в
4 раза.
