11. Корреляция

Явления в природе и обществе находятся во взаимосвязи. Раз­личают две формы связи:

• Функциональную - отражает строгую зависимость процессов или явлений, и изменение какого-либо одного явления обязательно связано с изменением числовых значений другого явления на строго определенную величину (площадь круга зависит от радиуса круга…);

• Корреляционную - значению каждой средней величины одного признака соответствует множество случайных значений друго­го взаимосвязанного с ним признака (связь между ростом и массой тела человека; связь межу температурой тела и частотой пульса).

Практическое значение установления корреляционной связи состоит в выявлении причинно-следственной между факторными и результативными признаками.

Корреляционная связь бывает:

• Положительной - прямой (при увеличении одного признака увеличивается другой);

• Отрицательной - обратной (при увеличении одного показателя другой уменьшается).

Вычисление корреляции:

Метод Спирмена (ранги):

1. Можно использовать при открытых значениях вариант (<20; >15);

2. Можно использовать, если нет возможности измерить числовые значения вариант.

Пример:

Стаж работы в годах	Число травм на 100 работающих
до 1 года  1-2  3-4  5-6  7 и более	24  16  12  12  6

Стаж работы в годах	Число травм	Порядковые номера (ранги)		Разность рангов	Квадрат разности рангов
		X	Y	d(х-у)	d2
До 1 года	24	1	5	-4	16
1-2	16	2	4	-2	4
3-4	12	3	2,5	+0,5	0,25
5-6	12	4	2,5	+1,5	2,25
7 и более	6	5	1	+4	16
						Σ d2 = 38,5

Каждый из рядов парных признаков обозначить через "х" и через "у"

Величину каждого из признаков заменить ранговым (порядковым) номером. Порядок раздачи рангов в ряду "x" следующий: минимальному значению признака (стаж до 1 года) присвоен порядковый номер "1", последующим вариантам этого же ряда признака соответственно в порядке увеличения 2-й, 3-й, 4-й и 5-й порядковые номера.

 Аналогичный порядок соблюдается при раздаче рангов второму признаку "у".  В тех случаях, когда встречаются несколько одинаковых по величине вариант (например, в задаче-эталоне это 12 и 12 травм на 100 работающих при стаже 3—4 года и 5—6 лет, порядковый номер обозначить средним числом из суммы их порядковых номеров - (2 + 3)/2 = 2,5.  Таким образом, числу травм "12" и "12" (признаку) следует раздать ранговые номера одинаковые — "2,5".

Определить разность рангов d = (х — у);

Разность рангов возвести в квадрат (d²) и получить сумму квадратов разности рангов Σ d².

Произвести расчет коэффициента ранговой корреляции по формуле:

 

где n — число сопоставляемых пар вариант в ряду "x" и в ряду "у"

Метод Пирсона (квадраты):

1. Применяется, когда требуется точное установление силы связи между признаками;

2. Применяется, когда признаки имеют только количественное выражение.

Пример:

Месяц года	Средняя температура воздуха (Со) (x)	Среднее количество детей, умерших от острых кишечных инфекций (в день) (y)	dx	dy	dx2	dy2	dx · dy
Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь	5 2 4 8 15 17 18 17 15 9 6 3	5,0 5,5 6,2 5,4 6,5 9,6 11,2 15,3 14,9 13,0 7,0 6,6	- 4,9 - 7,9 - 5,9 - 1,9 5,1 7,1 8,1 7,1 5,1 - 0,9 - 3,9 - 6,9	- 3,8 - 3,3 - 2,6 - 3,4 - 2,3 0,8 2,4 6,5 6,1 4,2 - 1,8 - 2,6	24,01 62,41 34,81 3,61 26,01 50,41 65,61 50,41 26,01 0,81 15,21 47,61	14,44 10,89 6,76 11,56 5,29 0,64 5,76 42,25 37,21 17,64 3,24 6,76	18,62 26,07 15,34 6,46 - 11,73 5,68 19,44 46,15 31,11 - 3,78 7,02 17,94
n = 12	Σ = 119,0 Мх = 9,9	Σ= 105,2 Му = 8,8			Σ=406,92	Σ=162,44	Σ=178,32

d_x = x - М_х

d_y = y – М_y

Вычисление коэффициента корреляции:

r_xy = Σ d_x · d_y / Σ d_x² · d_y² = 178,32 / 406,92 · 162,44 = +0,7

Расчет ошибки коэффициента корреляции:

m_r = ± 1 – r²_xy / n – 2 = ± 1 – 0,49/ 12 – 2 = ± 0,51/10 = ±0,226

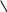
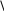
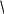
Оценка достоверности коэффициента корреляции:

t = r_xy / m_r = 0,7 / 0,226 = 3,1

12. Динамические ряды и их анализ + преобразование

Динамический ряд - совокупность однородных статистических величин, показывающих изменение явления на протяжении определенного промежутка времени.

Динамические ряды характеризуют изменение показателей здоровья – уровень снижения (роста) заболеваемости, травматизма; физического развития; демографические сдвиги (рождаемости, общей и младенческой смертности и др.).

В каждом ряду динамики имеется два основных элемента:

1) показатель времени - t;

2) соответствующие им уровни (числа, из которых состоит динамический ряд) развития изучаемого явления – y.

В зависимости от того, как выражают уровни ряда состояние явления на определённые моменты времени или его величину за определённые интервалы времени, различают соответственно моментные и интервальные ряды динамики:

Моментный ряд состоит из величин, характеризующих размеры яв­ления на определенные даты - моменты (например, на начало года – на 01.01.2020 г., или конец года – 31.12.2019 г.).

Интервальный ряд - ряд чисел, строящийся из величин, учтенных не на одну дату, а за определенный отрезок времени (например, за сутки, месяц, год и т.п.).

Поскольку в ходе обработки динамического ряда важнейшей задачей является выявление основной тенденции развития явления и сглаживание случайных колебаний, для решения этой задачи в статистике существуют особые способы, которые называют методами выравнивания.

Более точным способом отображения тенденции динамического ряда считается аналитическое выравнивание - выравнивание с помощью аналитических формул.

Выделяют три основных способа обработки динамического ряда:

1). Укрупнение интервала, при котором производится увеличение протяженности временных промежутков, и рассчитываются новые значения уровней ряда за счет суммирование дан­ных за ряд смежных периодов, уровни которых заменяют полученной суммой

Месяц	Число случаев заболеваний	Число случаев заболеваний по кварталам
1	288	288 + 388 + 271 = 947
2	388
3	271
4	260	260 + 230 + 129 = 619
5	230
6	129
7	133	133 + 137 + 231 = 501
8	137
9	231
10	380	380 + 370 + 530 = 1280
11	370
12	530
Всего	3347

2). Вычисление групповой средней производят путем суммирова­ния смежных уровней соседних периодов и делением суммы на число слагаемых, при этом, количество уровней ряда, взятых для расчета групповой средней, заменяют на полученную среднюю величину.

Годы	Процент расхождения диагнозов	Групповая средняя
2011	11,0	(11,0 + 9,8) : 2 = 10,4
2012	9,8
2013	8,0	(8,0 + 9,2) : 2 = 8,6
2014	9,2
2015	8,2	(8,2 + 8,6) : 2 = 8,4
2016	8,6
2017	8,5	(8,5 + 7,9) : 2 = 8,2
2018	7,9

3). Вычисление скользящей средней. Данный метод применяется для характеристики тенденции развития исследуемой статистической совокупности и основан на расчете средних уровней ряда за определенный период.

Месяцы	Число случаев пневмонии	Сумма трех уровней	Скользящая средняя
1	10		-
2	12	10 + 12 + 14 = 36	36 : 3 = 12
3	14	12 + 14 + 13 = 39	39 : 3 = 13
4	13	14 + 13 + 15 = 42	42 : 3 = 14
5	15	13 + 15 + 20 = 48	48 : 3 = 16
6	20	15 + 20 + 16 = 51	51 : 3 = 17
7	16	20 + 16 + 18 = 54	54 : 3 = 18
8	18	16 + 18 + 20 = 54	54 : 3 = 18
9	20	18 + 20 + 22 = 60	60 : 3 = 20
10	22	20 + 22 + 18 = 60	60 : 3 = 20
11	18	22 + 18 + 11 = 51	51 : 3 = 17
12	11		-

При этом варианте каждую отдельную величину ряда (кроме начальной и конечной) заменяют средней арифметической из нескольких величин.

Анализ динамических рядов применяется для описания поведения показателей во времени, и определения применимости данных для точного прогнозирования изменений. Кроме того, он используется для выявления неожиданного изменения формы временного ряда. Основным условием для получения правильных выводов при анализе рядов динамики является сопоставимость его элементов.

Анализ динамических рядов (иногда называемый анализом трендов) представляет набор методов для изучения последовательных во времени групп наблюдений за показателями качества – случайных процессов.

1) Абсолютный прирост или убыль (абсолютный размер разности уровней) - разность между последующим и предыдущим уровнем. Этот показатель представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. Он дает возможность установить, насколько за единицу времени в среднем должен увеличиваться уровень ряда (в абсолютном выражении), чтобы, отправляясь от начального уровня за данное число периодов (например, лет) достигнуть конечного уровня.

2) Темп роста или снижения - процентное отношение последующего уровня к предыдущему. Этот показатель дает возможность анализировать относительную скорость происходящих изменений, выраженную в процентах и применяется для характеристики изменения процесса одного периода по отношению к предыдущему периоду.

3) Темп прироста или убывания - процентное отношение абсолют­ного прироста (или снижения) к предыдущему уровню и обозначается знаком «+» (прирост) или знаком «-» (убыль). Темп прироста (убывания) равен темпу роста (снижения) минус 100.

4) Для анализа динамического ряда используются также показатели наглядности, хотя следует помнить, что для коэффициента нагляднос­ти необязательны взаимосвязанные динамические изменения.

При сравнении динамических рядов с разными исходными уровнями (например, средними, интенсивными, абсолютными), используется показатель значение 1% прироста (убыли). Он рассчитывается, как отношение абсолютного прироста к темпу прироста за каждый период, но в практике общественного здоровья и здравоохранения используется крайне редко.