
Билеты / матан
.pdf
30. Замена переменных в кратном интеграле. Полярные, цилиндрические и сфе- |
||||||||||||||||||||
рические координаты. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пусть А ᶰ-измеримо по Жордану; (x) = ( , … ) (A) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
̅̅̅̅̅ |
||
Пусть задано n скалярных функций |
|
|
= |
|
|
( , … , |
||||||||||||||
|
|
|
), k = 1, n опр-х и диф-х в |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||
ᶰ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Это означает, что задана одна векторная функция : ᶰ → ᶰ |
||||||||||||||||||||
|
|
|
|
|
|
|
(t): → A , (t) С1( ) |
|||||||||||||
Опр. Пусть задана векторная ф (t): ᶰ → ᶰ, |
(t) С1( ) |
|||||||||||||||||||
|
|
|
|
|
1( ) |
|
|
1( ) |
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Тогда |
( ) = |
|
2( ) |
|
2( ) |
|
|
… |
|
|
наз |
матрицей Якоби точки = |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
( ) |
|
( ) |
|
( ) |
|
|
|
|
|
||||||
|
|
|
|
( |
1 |
|
|
2 |
|
|
|
|
|
) |
|
|
|
|
||
( , … , ), а ее определитель det ( ) |
= ‖ |
|
‖ |
= ( ) наз Якобианом ( ) = |
||||||||||||||||
|
||||||||||||||||||||
|
|
|||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|||||
( 1,…, ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
( 1,…, ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Т 1.5 О замене переменных в кратном интеграле Пусть ᶰ- открытое, измеримое множество
Пусть задана векторная ф ( ): → A ᶰ, где А-открытое, измеримое мнво и отображение : → A биективно(взаимооднозн.)
Пусть (t) С1( ), а скалярная ф (x) = ( |
, … )( : → )инт на ( |
||||
|
|
|
1 |
|
|
(A)) ; |
|
|
|
|
|
Пусть ( ( )) |det (t))| (t); |
|
|
|
||
|
|
|
|
|
|
Тогда |
справедлива |
формула |
замены |
переменных∫ |
( ) = |
∫ ( ( ))|det (t))|
(Отображение : → A, удовл усл. Т 1.5 наз. регулярным отображением) ►без док-ва ◄
Опр. При замене переменных в кратном интеграле новые независимые переменные 1, … , наз криволинейными координатами.
Наиболее распространённые криволинейные координаты в пространстве.
1.Цилиндрические координаты
=
{ = |
0≤ ≤∞,0≤ ≤ |
|
||||||||
−∞≤ ≤∞ |
|
|
||||||||
|
|
|
|
= |
|
|
||||
|
|
|
|
|
− |
0 |
||||
|
|
|
|
|
( , , ) |
|||||
|
( |
|
) |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
= (r, φ, z) |
= | |
|
0| = |
|||||
|
|
|||||||||
|
|
|
|
|
|
|
0 |
0 |
1 |
|
= = φdz
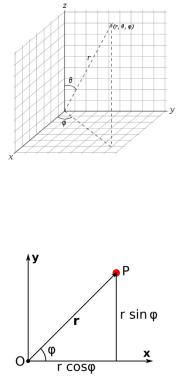
2. |
Сферические координаты |
|
|||||||
( , , ) → ( , , ), |
0 ≤ ≤ ∞, 0 ≤ ≤ |
||||||||
0 ≤ ≤ (− /2 ≤ ≤ /2) |
|||||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
= |
||||
|
|
|
|
|
{ = |
||||
|
|
|
|
|
|
= |
|
||
|
( ) = |
( , , ) |
= |
|
|
|
|||
|
(r,θ,φ) |
|
|
||||||
|
|
|
|
|
|
||||
|
|
− |
|||||||
| |
|
| = 2 |
|||||||
|
|
|
− |
0 |
|
||||
3. |
Полярные координаты |
|
|||||||
|
|
|
|
|
= |
|
|||
|
|
|
|
{ = , > 0 |
|||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
−| = |
|||
|
= | |
| = | |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
31. Криволинейный интеграл I рода и его свойства. Его вычисление.
Рассматриваем в 2 (в n аналогично). Рассмотрим на Oxy:
: {x = x(t) , y = y(t)}, t [α,β].
x(t),y(t) C1[α,β] (непрерывно диф-мы по 1ой производной),
x’2(t)+y’2(t) ≠ 0 t [α,β]. – простая, гладкая, незамкнутая кривая. Пусть – измеримое по Жордану мн-во в 1 – спрямляемая кривая(можно вычислить
длину). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим разбиение P = { } |
|
опр. на [α,β]. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
Выберем точки |
[ |
|
|
, ], |
|
̅̅̅̅̅ |
|
|
||||||
|
|
i 1, . Получим разбиение (P, ). Таким отвечают |
||||||||||||
|
|
|
|
|
−1 |
|
|
|
|
|
|
|||
точки ( ( ), ( )) L |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Об. |
|
= |
|
- длина дуги. Точкам отвечают точки ( ), ( ) . Пусть |
||||||||||
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
задана |
функция |
|
z = |
|
f(x,y). |
Составим интегральную |
сумму |
Ϭ(f, P, ) = |
||||||
∑ |
( ( ), ( )) |
|
|
|
|
|
|
|
|
|||||
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Об. λ(P) = max , 1 i n |
|
|
|
|
|
|||||||||
Опр. 1 Если lim |
|
Ϭ(f, P, ) = , то он наз-ся криволинейным инт-лом I рода от ф- |
||||||||||||
|
|
|
(Р) 0 |
|
|
|
|
|
|
|
|
|
||
ции f по кривой ( ε>0 = (ε)>0 : разбиения (Р, ) : (Р) < => | Ϭ(f, P, ) – I| < ε)
Об. I=∫/ ( , )
Т 2.1
Пусть
1): {x=x(t) , y=y(t)}, t [α,β]; x(t),y(t) C1[α,β]; x’2(t)+y’2(t)≠0 t [α,β];
t [α,β];
2)f(x,y) непрерывна на , – простая(не имеющая точек самопересечения), незамкнутая(начало и конец не совпадают).
Тогда криволинейный ин-л 1 рода от ф-ции f(x,y) по кривой L и справедливо:
|
∫/ ( , ) = |
∫β/ ( ( ), ( )) √ |
|
|
|
|
|
′2 |
( ) + ′2( ) |
(1) |
|||
|
|
α |
|
|
|
|
► Отметим, что определенный ин-л Римана в правой части р-ва (1) |
, т.к. подын- |
|||||
тегральная ф-ция непрерывна. |
|
|
|
|||
Об. |
lim Ϭ(f, P, ) = . |
|
|
|
|
|
|
(Р) 0 |
|
|
|
|
|
Рассмотрим разб. (Р, ) |
|
кривой L и составим интегральную сумму Ϭ(f, P, ) = |
|||||||||||||||||||||||||||||||||||||
∑ |
( ( ), ( )) |
|
и применим ф-лу длины дуги кривой(из 1курса) |
|
= |
||||||||||||||||||||||||||||||||||
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′2 |
( ) |
|
′2 |
( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∫ −1 √ |
+ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)) ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Получаем Ϭ(f, P, ) = |
|
|
( ( ), ( |
√ ′2( ) + ′2( ) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Применим |
|
св-во |
|
|
аддитивности: |
|
( |
( ), ( ) |
) |
√ |
′2( ) |
+ |
′2( |
) |
= |
||||||||||||||||||||||||
|
|
|
|
I=∫α |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
∑ |
ti |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
( ), ( ) |
) |
√ |
′2 |
( ) |
+ |
′2( |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
∫ti−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Составим разность:
| Ϭ(f, P, ) − | =

ti
=| ∑ ∫ ( ( ), ( )) √ ′2( ) + ′2( ) –
ti−1
∫titi−1 ( ( ), ( )) √ ′2( ) + ′2( ) |=
(св − во линейности)
=
|
∑ |
|
ti |
|
|
|
ti |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= | |
∫ |
[ ( ( ), ( )) − |
∫ |
|
( |
( |
|
) |
, |
( ) |
] √ |
′2 |
( |
) |
+ |
′2 |
( |
) |
| |
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
=1 |
ti−1 |
|
|
ti−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
(св − во аддитивности ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
|
ti |
|
|
|
|
ti |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
| [ ( ( ), ( )) − ∫ |
|
( |
( |
|
) |
, |
( ) |
) ] | √ |
′2( ) |
+ |
′2( |
) |
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||
|
=1 |
ti−1 |
|
|
|
ti−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x(t), y(t) C1[α,β] => x'(t), y'(t) C[α,β] – непрерывны => x’(t), y’(t) – равномерно непрерывны на [α,β].
Заметим, |
|
что |
|
|
|
|
λ(P) = max |
|
→ 0 |
=max |
→0 |
, т.к. |
|
= |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′2 |
( ) |
|
|
′2 |
( |
) |
|
|
|
|
|
|
|
′2( ) |
|
′2 |
( |
) |
|
|
|
|
|
|
||||||||
∫ √ |
+ |
≥ m , где m = min√ |
+ |
на [α,β] |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M |
≥ |
|
≥ m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Т.о. ε>0 = (ε)>0 : < |
| ( ( ), ( )) – ( (t), ( ))| < |
|
, l – длина кривой |
||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∑ =1 ∫ti √ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
= |
∑ =1 = ◄ |
|
|
|||||||||||||||||||||||||||||
L => | Ϭ − I| < |
|
′2( ) + ′2( ) |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ti−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Замечание 1: Если – кусочно-гладкая, а f(x,y) – кусочно-непрерывная, то Т.1 |
|||||||||||||||||||||||||||||||||
остается в силе. Если – замкнутая кривая, то Т 2.1 |
остается в силе. |
|
|
||||||||||||||||||||||||||||||||
|
|
Замечание 2: : {y=y(x), x [a,b]} ∫ |
( , ) = ∫ ( , ( ) √1 + ′2( ) |
|
|||||||||||||||||||||||||||||||
|
|
Замечание 3 L: r=r(φ) |
α≤ φ ≤β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
∫ ( , ) = ∫ ( φ, φ) √ 2(φ) + ′2(φ) φ |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Св-ва криволин. интеграла I рода. Вследствие Т 2.1, те же св-ва, что и у интеграла Римана.
1.Линейность:
∫( , ) + ( , ) = ∫ ( , ) + ∫ ( , )
|
|
|
2. Аддитивность:
∫ ( , ) =∫ ( , ) + ∫ ( , )
3. Св-во с модулем:
|∫ ( , ) |≤ ∫ | ( , )|
4.Ф-ла среднего значения:
Если f(x,y) непрерывна на , то
(x’,y’) ∫ ( , ) = ( ′, ′) ∫ = f(x’,y’) *
32. Криволинейный интеграл II рода. Его вычисление.
Рассматриваем в 2 (в n аналогично). Рассмотрим на Oxy:
: {x = x(t) , y = y(t)}, t [α,β].
x(t),y(t) C1[α,β] (непрерывно диф-мы по 1ой производной),
x’2(t)+y’2(t) ≠ 0 t [α,β]. L – простая(не имеющая точек самопересечения), гладкая, незамкнутая кривая. Пусть – измеримое по Жордану мн-во в 1 – спрям-
ляемая кривая(можно измерить длину). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Рассмотрим разбиение = { } |
опр. на [α,β]. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выберем точки [ |
|
, ], |
|
|
|
|
̅̅̅̅̅ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
i 1, . . Получим разбиение (P, ). Таким отвечают |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
точки ( ( ), ( )) L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Об. |
|
= |
|
- длина дуги. Точкам отвечают точки ( ), ( ) . Пусть |
||||||||||||||||||||||||||||
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
на кривой L заданы непрерывные ф-ции P (x,y) и Q(x,y). |
|
|
|
|
|
|||||||||||||||||||||||||||
∆ = − |
, = ( ), ∆ = − |
= ( ) |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Составим интегральные суммы: Ϭ1(P, , ) = |
∑ |
|
( ( |
), ( )) |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
||
Ϭ2(Q, , ) = ∑ |
|
( ( |
), ( )) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Об. λ(P) = max , 1 i n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Опр. 1 Если |
lim |
|
Ϭ |
[ |
lim |
Ϭ |
|
|
], то он наз-ся криволинейным инт-лом II рода от |
|||||||||||||||||||||||
|
|
|
( ) 0 |
1 |
( ) 0 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ф-ции P(x,y) [Q(x,y)] по кривой L и обозначается: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
lim |
|
Ϭ = |
∫/ ( , ) , |
|
lim |
|
|
Ϭ |
2 |
= ∫/ ( , ) |
||||||||||||||||
|
|
|
|
|
( ) 0 |
1 |
|
|
|
|
|
|
|
( ) 0 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Сумма ∫/ |
( , ) + ( , ) наз-ся общим криволин. инт-лом II рода. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Физический смысл |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
) |
|
|
|
( |
, |
) |
= |
{ ( |
|
) |
, |
( |
, |
)} |
|||
|
|
|
|
|
|
|
A = ∫ ( |
|
|
, |
, ) , |
|
|
|
, |
|
, |
|||||||||||||||
= { , } - работа силы вдоль кривой.
Т 2.2
Пусть
1): {x=x(t) , y=y(t)}, t [α,β]. x(t),y(t) C1[α,β]. x’2(t)+y’2(t)≠0 t [α,β].
2)Q(x,y), P(x,y) непрерывные на , – простая, незамкнутая, спрямляемая(измеряемая) кривая.
Тогда криволинейные интегралы 2 рода и справедливо р-во:
∫/ |
( , ) = |
∫β/ |
( ( ), ( )) ′( ) |
(2) |
|||
|
∫/ |
|
α |
|
∫β/ |
|
|
|
( , ) = |
( ( ), ( )) ′( ) |
(2') |
||||
|
|
|
|
|
α |
|
|
Докажем (2) ( (2’) аналогично)
► Отметим, что определенный интеграл Римана в правой части р-ва (2) , т.к. P(x(t),y(t)), x’(t) непрерывны на [α,β] . Рассмотрим разб. ( , ) отрезка [α,β] и со-
ставим |
интегральную |
сумму Ϭ(P, , ) = ∑ |
|
( ( ), ( )) . Учтем, что |
||||||||
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
∆ = − |
= ( ) − ( |
|
) = ∫ |
′( ) . |
|
|
|
|
||||
|
|
−1 |
|
−1 |
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получаем Ϭ(P, , ) = ∑ |
( ( ), ( )) ∫ |
′( ) |
|
|
||||||||
|
|
|
|
=1 |
|
|
|
−1 |
|
|
|
|
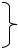
Применим св-во аддитивности:
I ≡ ∫αβ/ ( ( ), ( )) ′( ) = ∑ =1 ∫titi−1 ( ( ), ( )) ′( )
Составим разность:
| Ϭ(P, , ) − | =
= | |
∑ |
|
|
∫ |
ti |
|
|
( ( ), ( )) ′( ) - |
|
∑ |
∫ |
ti |
|
( |
( ), ( ) |
) |
|
′( ) |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
=1 |
ti−1 |
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
ti−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(св − во линейности) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
ti |
|
|
|
|
|
= |
ti |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
= | |
∑ |
|
|
∫ |
|
[ |
( ( ), ( )) − ∫ |
|
|
|
( ) |
|
( ) |
) ] ′( ) | |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
=1 |
|
ti−1 |
|
|
|
|
ti−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(св − во аддитивности ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
|
∫ |
ti |
| [ ( ( ), ( )) |
− ∫ |
ti |
|
|
|
( ) |
( ) |
) ] | | ′( )| |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
=1 |
|
ti−1 |
|
|
|
|
|
|
ti−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I т.Вейерштрасса |
x’(t) – ограничена на [α,β], |
||||||||||||||||||||||
x`(t) C1[α,β] => x'(t) C[α,β] – непрерывна |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
т.е. > 0: ′( ) ≤ [ , ]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
P(x(t), y(t)) непрерывна на [ , ] |
т.Кантора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
P(x(t),y(t)) равномерно непрерывна на |
||||||||||||||||||||||||||||||||||||||||||
[ , ], т.е. ε>0 = (ε)>0 : | t| < | ( ( ), ( )) – ( (t), ( ))| < |
|
|
. Заме- |
||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( − ) |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тим, что λ( ) = max |
|
→ 0 |
= max |
→0 ; |
|
|
= ∫ |
√ |
′2( ) |
+ |
′2( |
) |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ti |
|
|
|
|
|
|
|
|
|
|
|
|
|
Т.о. ε>0 = (ε)>0 : ( , ): < | Ϭ(P, , ) − I| < |
∑ =1 ∫ti−1 |
|
c = |
◄ |
|||||||||||||||||||||||||||||||||||||||
( − ) |
|||||||||||||||||||||||||||||||||||||||||||
Замечание 1: Если – кусочно-гладкая, а Q и P – кусочно-непрерывная, то Т |
|||||||||||||||||||||||||||||||||||||||||||
2.2 остается в силе. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Замечание 2: : {y=y(x), x [a,b]} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ ( , ) + ( , ) = ∫[ ( , ( )) 1 + ( , ( )) ′( )] |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание 3: Крив. интеграл II рода, в отличие от I, зависит от того, в каком |
|||||||||||||||||||||||||||||||||||||||||||
направлении протекает кривая . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
∫ ( , ) + Q(x, y)dy = − |
|
|
|
∫ ( , ) + Q(x, y)dy |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Если – замкнутая, то Т 2.2 остается в силе. Но за направление принимаем такое, чтобы область, лежащая внутри контура, оставалась слева.
Замечание 4. В силу Т 2.2, крив. интеграл II рода имеет св-ва:
1)Линейность (+)
2)Аддитивность (+)
3) |
Св-во с модулем |
вообще говоря, не выполняется |
|
4) |
Формула среднего значения |
||
|

33. Формула Грина.
Опр. Область σ̅ называется односвязной, если её граница является замкнутой кривой Опр. Область σ̅ 2 называется простейшей, если она одновременно:
1)Односвязна;
2)Ограничена;
3)прямая, || осям координат и пересекающая область σ̅, пересекается с ней по некоторому отрезку;
4)Её граница ∂σ непрерывно-кусочно гладкая кривая, т.е. ∂σ состоит из конечного числа гладких кривых.
Опр. Область ̅σ 2 называется простой, если её можно представить в виде объединения конечного числа простейших областей
Т 2.3. Формула Грина Пусть σ простая область и =∂σ-граница области σ̅ с положительным
направлением её обхода. Пусть ф. P(x, y) и Q(x, y) непрерывна вσ̅ и имеет в σ̅
непрерывные частные производные ∂P и ∂Q, тогда
∂y ∂x
P(x, y)dx + Q(x, y)dy= ∫ ∫ (∂Q∂x , ∂P∂y) dx dy
σ
►1) Для простейшей области
Рассмотрим:
|
|
|
|
y2(x) |
|
|
|
|
|
|
|
|
|
|
|
-∫ ∫ ( |
∂P |
) dx dy = - ∫b dx ∫ |
∂P |
dy=-∫b dx P(x, y)|y2(x) |
= |
|
|
|
|
||||||
|
|
|
|
|
|
||||||||||
|
|
|
∂y |
a |
∂y |
a |
|
y |
(x) |
|
|
|
|
|
|
σ |
|
|
y1(x) |
|
|
1 |
|
|
|
|
|
|
|
||
-(∫ |
b |
|
|
|
( |
|
= − ∫ |
|
( |
|
) |
+ ∫ |
( |
) |
= |
|
|
|
|
|
|
|
|||||||||
|
( , y2( ))-P(x, y1( ))) = По Т2.2) |
|
, |
|
, |
||||||||||
a |
|
|
|
|
|
ABC |
|
|
|
CDA |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ CDA ( , ) + ∫ ABC ( , ) = P(x, y) dx

Аналогично:
|
|
|
x2(y) |
|
|
∫∫ ( |
∂ |
) dx dy=∫d dy ∫ |
∂Q |
dx= |
|
|
|
||||
σ |
∂x |
c |
x (y) |
∂x |
|
|
|
|
1 |
|
|
=(∫cd (x2( ), )-Q( 1( ), ) = (по Т 2.2 о криволинейном инт − ле 2 рода) =
= ∫ CD ( , ) + ∫ DAB ( , ) = Q(x, y) dy
Складывая, получим формулу Грина
2) Пусть теперь ̅σ-простая область, состоящая из 2-ух простейших областей:
̅σ = ̅σ1 ̅σ2(не имеет общих внутренних точек)
1
Об. =∂σ
=∂σ1=∂σ1
+ = ∫ ABC( + ) + ∫ ( + ) = |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
∫ −//− … +∫ −//− … +∫ CA −//−… +∫ −//− … = 1 |
… 2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
=0 |
|
|
|
|
|
|
|
|
|
|
|
По 1) Т 2.3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ = |
( |
|
− |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
)dxdy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ = |
( |
|
− |
|
)dxdy |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
∫ |
( , ) + ( , ) = 1 |
+ + 2 |
+ = 1( |
|
− |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
) + |
( |
|
− |
|
) =(аддитивная кривая и интегр. ̅σ)= ( |
|
− |
|
)dxdy |
||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
По индукции Т2.3 распространяется на простую область ◄
Следствие: Пусть ф. P(x,y) и Q(x,y) на обл. σ уд. Условиям Т 2.3. Тогда следующие утверждения эквивалентны:
I.Для замкнутого контура σ, ( , ) + ( , ) = 0
II.Для точек A,B σ ∫AB ( , ) + ( , ) не зависит от пути интегр.
III.Выражение ( , ) + ( , ) является полным дифференциалом, т.е.
в обл. σ ф. U(x,y): dU(x,y)=P(x,y)dx+Q(x,y)dy ∫AB ( , ) +
( , ) = ∫AB =U(B)-U(A) |
|
IV. Пусть обл. σ-односвязна = |
( , ) σ |

34. Понятие поверхности. Площадь поверхности. Вычисление площади поверхности с помощью двойного интеграла.
Пусть в замкнутой области ̅σ 2 заданы 3 непрерывные функции: x=x (U, V),y=y (U, V),z=z (U, V) (1)
Опр. Множество P= {(x(U, V), y(U, V), z(U, V)): (U,V) ̅σ 2} точек 3х-мерного про-
странства, координаты которых задаются уравнениями (1), будем называть простой параметрически-заданной поверхностью если различным (U, V) σ̅ соответ-
ствуют различные (x, y, z) P(непрерывное взаимнооднозначное соответствие
(σ̅ 2 → P 3)
Опр. Поверхностью будем называть объединение конечного числа простых поверхностей
Уравнение поверхности в векторной форме:
̅
Радиус-вектор r̅=i̅x+ j̅y+kz
z
r
|
|
(x, y, z) P, учитывая (1) получаем |
|
x |
|
̅ |
|
y |
r̅(U,V)= i̅x(U,V)+ j̅( , )+kz(U,V) (2), |
||
где |
r̅(U,V)-векторная функция двух аргументов (U,V) |
||
|
|||
Пусть, ф-ии |
|
x=x(U, V), y=y(U, V), z=z(U, V) непрерывно дифф. В ̅σ. |
Тогда r̅(U,V0), при фиксированном V=V0 становится непрерывно-дифф. кривая на поверхности P (коорд. линия)
′ |
′ |
̅ |
|
′ |
. Аналогично при фиксирован- |
Касательный вектор этой кривой r̅=i̅ |
+j̅ |
+k |
|
||
u |
|
|
|
|
|
ном U=U0 ур-е r̅(U0,V)-определяет другую координатную линию( непрерывно-
|
′ |
′ |
̅ |
|
′ |
. В точке |
дифф. кривую на P, её касательный вектор имеет вид r̅=i̅ |
+j̅ |
+k |
|
|||
|
|
|
|
|
|
|
0(x0, y0, z0), где x0 = (U0, V0), y0=y(U0, V0), z0=z(U0, V0), обе эти координатные линии будут пересекаться.
Опр. Точка параметрически заданной поверхности наз-ся особой, если в этой
|
′ |
|
̅′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
̅′ |
|
̅ |
и . Отметим, что точка не является особой |
|
̅ |
|
|||||||||||||||||||||||||||||
точке вектора |
|
|
[ , ] ≠0. |
||||||||||||||||||||||||||||||
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
|||
Опр. Если поверхность P задана уравнением (1) и формулой (2) непрервыно-дифф. |
|||||||||||||||||||||||||||||||||
в σ и P не имеет особых точек, то она называется гладкой. |
|
|
|
|
|
|
|||||||||||||||||||||||||||
Если точка ̅ = r̅(U |
|
|
|
|
|
|
|
|
̅′ |
(U |
|
, V ) определяют единственную плоскость, которая |
|||||||||||||||||||||
0 |
, V ) и |
0 |
|||||||||||||||||||||||||||||||
0 |
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
является касательной плоскостью к поверхности P в точке μ0(x0, y0, z0) |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
̅′ |
|
|
|
|
|
|
|
|
|
|
′ |
̅′ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̅ |
|
|
|
|
|
|
|
|
|
|
|
|
̅ |
|
|
|||
Ур-е касательной плоскости r̅-r̅ , , - компланарны |
|
|
(r̅-r̅ , , )=0 или |
||||||||||||||||||||||||||||||
|
|
|
|
|
− x0 |
|
|
0−uy0 |
− z0 |
|
|
|
|
|
|
0 u |
|
|
|||||||||||||||
|
|
|
′ |
(U |
0 |
, V ) |
|
′ |
(U |
0 |
, V ) |
′ |
(U |
0 |
, V ) |
|=0 |
|
|
или |
|
|
|
|||||||||||
|
|
|
| |
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
||||||||||
|
|
|
′ |
(U , V ) |
|
′ |
(U |
0 |
, V ) |
′ |
(U |
0 |
, V ) |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
0 |
|
|
0 |
′ |
|
′ |
|
|
|
|
|
|||||||
|
|
|
x-x |
|
| |
′ |
′ |
|+y-y |
|
|
′ |
′ |
|+z-z |
|
|=0 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
| |
|
| |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
′ |
′ |
|
|
|
0 |
′ |
′ |
|
|
0 |
′ |
|
′ |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
B |
|
|
|
C |
|
|
|
|
|
|
|
|
|
|||
A( − x0)+B( − y0)+C(( − z0)=0 — касательная плоскость к поверхности P в точке μ0.

Нормаль к касательной пл. точки r̅(U0, V0) и единичный вектор нормали ̅ = { , , }
n̅ = ± { |
|
|
A |
; |
|
|
|
; |
|
|
C |
|
}—направляющие косинуса. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
2 |
2 2 |
2 |
2 2 |
2 |
2 2 |
||||||||
|
√A |
+B +C |
|
√A |
+B +C |
|
√A |
+B +C |
|
|
|||
Т.к. ф-и x=x(U, V), y=y(U, V), z=z(U, V) имеют непрерывные частные производные, то ABC-непрервные. В этом случае говорят, что на поверхности P задано непрерывное поле нормалей.
Площадь поверхности
Пусть P-гладкая огр. поверхность, разобьём её с помощью кусочно-гладких кри-
̅̅̅̅̅
вых на конечное число n частей Pi=(i = 1, n) так, чтобы каждая часть Pi однозначна проектировалась на касательную пл-ть, проведённую в точку Pi(предполагается, что такое рубление возможно)
На каждой части Pi выберем произв. точку μ и проведем через неё касательную плоскость к поверхности. Пусть S −площадь проекции Pi на касат. плоскость(эта проекция огранич. Кусочно-гладкими кривыми измеримо по Жордану)
n |
̅̅̅̅̅ |
Составим сумму: σ( , М)=∑i=1 |
Si Об. λ = max di-диаметр Pi, i = 1, n |
Опр. Если lim σ( , М)= (P)=S, то он называется площадью поверхности P, а по-
λ→0
верхность P называется квадрируемой(измеримой)
Вычисление площади поверхности с помощью двойного интеграла Разобьем плоскость (U, V) линиями U=const, V=const прямоугольники. Рассмотрим прямоугольник Пi с вершиной в точке(U0, V0) и длинами сторон U и V, тогда прямоугольнику Пi при отображении (1) отвечает образ: криволинейный четырёхугольник на P заменяем приближенно криволинейный 4x-угольник паралле-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̅′ |
|
|
|
̅′ |
|
|
V. Получим для площади паралле- |
|||||||||||||||||||||||||
лограммом, построенном на векторах |
|
U, |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
лограмма S |
|
|
|
̅′ |
|
|
̅′ |
|
|
|
|
̅′ |
|
̅′ |
]| |
|
|
|
|
|
̅′ |
|
|
̅′ |
]| (П |
|
|
|
|
|
|
|
|
|
|
̅′ |
|
̅′ |
]| U V= |
||||||||||||||||||
= |[ |
U, |
|
V]|= |[ |
, |
U |
V=|[ |
, |
) или dS=|[ |
, |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
̅ |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i̅ |
|
j̅ |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̅′ |
|
̅′ |
|
|
k |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
̅ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
′ |
|
|
′ |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
+ C |
2 |
|
|
|
|
|
|
|
|
|
]=| |
|
|
|
|
|
|
|) |
|
|
|
|
|
|
||||||||||||||||
=|i̅ + j̅B + k | U V=√A + B |
|
|
U V (т.к.[ |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
′ |
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S= dS= √A2 |
+ B2 |
+ C2 |
U V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̅ |
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
̅ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Используя соотношение |[a̅, b]| |
|
+|(|(a, b)| |
=|a̅| |
|b| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
̅′ |
|
̅′ |
2 |
|
̅′ |
2 |
̅′ 2 |
|
̅′ |
|
̅′ 2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|[ |
, |
]| |
|
=( ) |
( ) |
|
-( |
, ) =EG-F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
G |
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̅′ |
|
2 |
|
|
′ |
2 |
|
|
′ 2 |
|
′ 2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S= √EG − F |
2 |
|
U V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+y |
+z |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E=( |
) =x |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Явное задание поверхности: |
|
|
|
|
z=f(x,y), (x,y) σ { |
= |
|
|
(подставим (1)) |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ( , ) |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i̅ |
j̅ |
|
|
̅ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
̅′ |
|
̅′ |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′2 |
|
|
|
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
′ |
|
|
|
|
|
′ |
|
|
|
̅ |
√ |
|
|
|
′ |
|
|
|
|
|
|
|
|||||||||||
|
2 |
+ B |
2 |
+ C |
2 |
|
|
]|=||1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
+ 1 |
|
|
|
|
||||||||||||||||||||||||
√A |
|
|
|
|
=|[ |
, |
|
|
|
||=|i̅(- |
|
)+ j̅(- |
)+ k|= |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S= √1 + ′ 2 |
+ ′ |
2dxdy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
