MINISTRY OF EDUCATION AND SCIENCE OF UKRAINE
KHARKIV NATIONAL UNIVERSITY OF RADIO ELECTRONICS
Department of ST
Report
on the implementation of laboratory work No. 5
"Numerical integration of functions"
In the discipline "Numerical integration of functions"
Complied by student KNT-23-1: Roman, Kravchenko
Kharkiv 2024 |
Accepted: P.E. Sytnikova,
|
Purpose of the work: acquisition of practical skills of numerical integration of functions. Comparative analysis of methods and methods of approximate calculation of definite integrals.
Work progress
Select the option of an individual task (table 1.2) according to the number of the student in the group list. Limits of integration a b, set independently.
Variant 11:
,
a = -2, b = 1, n = 4
Using the rules of integration, calculate the definite integral and obtain an exact solution to the problem.
Exact solution
Find approximate values of the definite integral using the formula of left rectangles, the formula of right rectangles, the formula of trapezoids, Simpson's formula. Set n = 4.
Left rectangles formula.
Let's divide the integration interval into n parts to find grid step h. And write down the formula
, where
.
Then
|
|
|
|
|
-2 |
-1.25 |
-0.5 |
0.25 |
1 |
Find the common values of the integral function:
-
-48
-5.25
-1.875
-4.969
-12
Let's apply the formula of left rectangles
Right rectangle formula.
Trapezius formula.
.
Then
Simpson formula.
.
Then
Choose n = 20 (number of partition segments) and calculate the approximate value of the integral using developed program by the formulas of the left and right rectangles, trapezoids and Simpson.
Program listing.
#include <iostream>
#include <vector>
constexpr double exact_answer = -25.65;
constexpr double left = -2;
constexpr double right = 1;
constexpr double a = -4;
constexpr double b = -1;
constexpr double c = 1;
constexpr double d = -4;
constexpr double e = -4;
constexpr int n = 20;
constexpr double h = (right - left) / n;
static double fx(double x)
{
return a * pow(x, 4) + b * pow(x, 3) + c * pow(x, 2) + d * x + e;
}
static double first_derivative(double x)
{
return 4 * a * pow(x, 3) + 3 * b * pow(x, 2) + 2 * c * x + d;
}
static double second_derivative(double x)
{
return 12 * a * pow(x, 2) + 6 * b * x + 2 * c;
}
static double third_derivative(double x)
{
return 24 * a * x + 6 * b;
}
static double fourth_derivative(double x)
{
return 24 * a;
}
static bool has_root_at_the_interval(const double left, const double right)
{
double left_value = first_derivative(left);
double right_value = first_derivative(right);
return left_value * right_value < 0;
}
static std::vector<double> find_the_critical_points()
{
std::vector<double> crit_points;
double temp_a = a * 12.;
double temp_b = b * 6.;
double D = temp_b * temp_b - 4. * temp_a * c * 2;
if (D > 0)
{
double x1 = (-temp_b + sqrt(D)) / (2. * temp_a);
double x2 = (-temp_b - sqrt(D)) / (2. * temp_a);
if (x1 >= left && x1 <= right && x2 >= left && x2 <= right)
{
if (x1 > x2)
std::swap(x1, x2);
crit_points.insert(crit_points.end(), { x1,x2 });
}
else if (x1 >= left && x1 <= right)
crit_points.emplace_back(x1);
else if(x2 >= left && x2 <= right)
crit_points.emplace_back(x2);
}
else if (D == 0)
crit_points.emplace_back(-temp_b / (2. * temp_a));
else
{
std::cerr << "\nThe given function has no critical points.\n" <<
"The separation of the roots CAN NOT be performed.\n";
exit(EXIT_FAILURE);
}
return crit_points;
}
static std::vector<double> find_intervals()
{
const std::vector<double> crit_points = find_the_critical_points();
std::vector<double> points;
double dx = 0.1;
double right_limit;
double left_limit;
const int MAX_ITERATIONS = 3000;
for (size_t i = 0; i < crit_points.size(); i++)
{
right_limit = crit_points[i] - dx;
left_limit = right_limit - dx;
int j = 0;
while (j <= MAX_ITERATIONS)
{
if (i > 0)
{
dx = std::abs(left_limit - crit_points[i - 1]) / 2;
if (std::abs(left_limit - crit_points[i - 1]) < 0.01)
break;
}
left_limit -= dx;
if (has_root_at_the_interval(left_limit, right_limit))
{
points.insert(points.end(), { left_limit, right_limit });
break;
}
++j;
}
}
left_limit = crit_points.back() + dx;
right_limit = left_limit + dx;
int j = 0;
while (j <= MAX_ITERATIONS)
{
++right_limit;
if (fx(left_limit) * fx(right_limit) < 0)
{
points.insert(points.end(), { left_limit, right_limit });
break;
}
++j;
}
return points;
}
static std::vector<double> combined_method()
{
std::vector<double> roots;
std::vector<double> intervals = find_intervals();
int k = 0;
for (size_t i = 0; i < intervals.size(); i += 2)
{
double a_k = (intervals[i] + intervals[i + 1]) / 2;
double b_k;
if (second_derivative(a_k) * third_derivative(a_k) < 0)
{
a_k = intervals[i];
b_k = intervals[i + 1];
}
else
{
b_k = intervals[i];
a_k = intervals[i + 1];
}
while (std::abs(a_k - b_k) > 2 * 0.001)
{
b_k = b_k - (second_derivative(b_k) * (a_k - b_k)) / (second_derivative(a_k) - second_derivative(b_k));
a_k = a_k - (second_derivative(a_k) / third_derivative(a_k));
++k;
}
roots.emplace_back((a_k + b_k) / 2);
}
return roots;
}
static double LeftRectangle()
{
double sum = 0.;
for (int i = 0; i < n; ++i)
sum += fx(left + i * h);
return h * sum;
}
static double RightRectangle()
{
double sum = 0.;
for (int i = 1; i <= n; ++i)
sum += fx(left + i * h);
return h * sum;
}
static double Trapezoidal()
{
double sum = (fx(left) + fx(right)) / 2.;
for (int i = 1; i < n; ++i)
sum += fx(left + i * h);
return h * sum;
}
static double Simpsons()
{
double sum = fx(left) + fx(right);
for (int i = 1; i < n; ++i)
{
if (i % 2 == 0)
sum += 2 * fx(left + i * h);
else
sum += 4 * fx(left + i * h);
}
return h * sum / 3.;
}
static double max_value_of_m1()
{
std::vector<double> crit_points = combined_method();
double value = std::max(std::abs(first_derivative(left)), std::abs(first_derivative(right)));
for (double number : crit_points)
value = std::max(value, std::abs(number));
return value;
}
static double LeftAndRightError()
{
double m1 = max_value_of_m1();
return h * (right - left) * m1 / 2.;
}
static double max_value_of_m2()
{
double crit_point = 6 * -b / (2. * 12 * a);
return std::max({ std::abs(second_derivative(left)), std::abs(second_derivative(right)), std::abs(crit_point) });
}
static double TrapezoidalError()
{
return pow(h, 2) / 12 * (right - left) * max_value_of_m2();
}
static double SimpsonError()
{
double m3 = std::abs(fourth_derivative( 24 * a));
return pow(h, 4) * (right - left) * m3 / 180;
}
int main()
{
std::cout << "Left Rectangle.\n\tAnswer: " << LeftRectangle() << '\n' << "\tMax error: " << LeftAndRightError() << '\n' << "\tAbsolute Error: " << abs(exact_answer - LeftRectangle()) << '\n';
std::cout << "\nRight Rectangle.\n\tAnswer: " << RightRectangle() << '\n' << "\tMax error: " << LeftAndRightError() << '\n' << "\tAbsolute Error: " << abs(exact_answer - RightRectangle()) << '\n';
std::cout << "\nTrapezoidal.\n\tAnswer: " << Trapezoidal() << '\n' << "\tMax error: " << TrapezoidalError() << '\n' << "\tAbsolute Error: " << abs(exact_answer - Trapezoidal()) << '\n';
std::cout << "\nSimpson's.\n\tanswer: " << Simpsons() << '\n' << "\tMax error: " << SimpsonError() << '\n' << "\tAbsolute Error: " << abs(exact_answer - Simpsons()) << '\n';
return 0;
}
Program’s output.
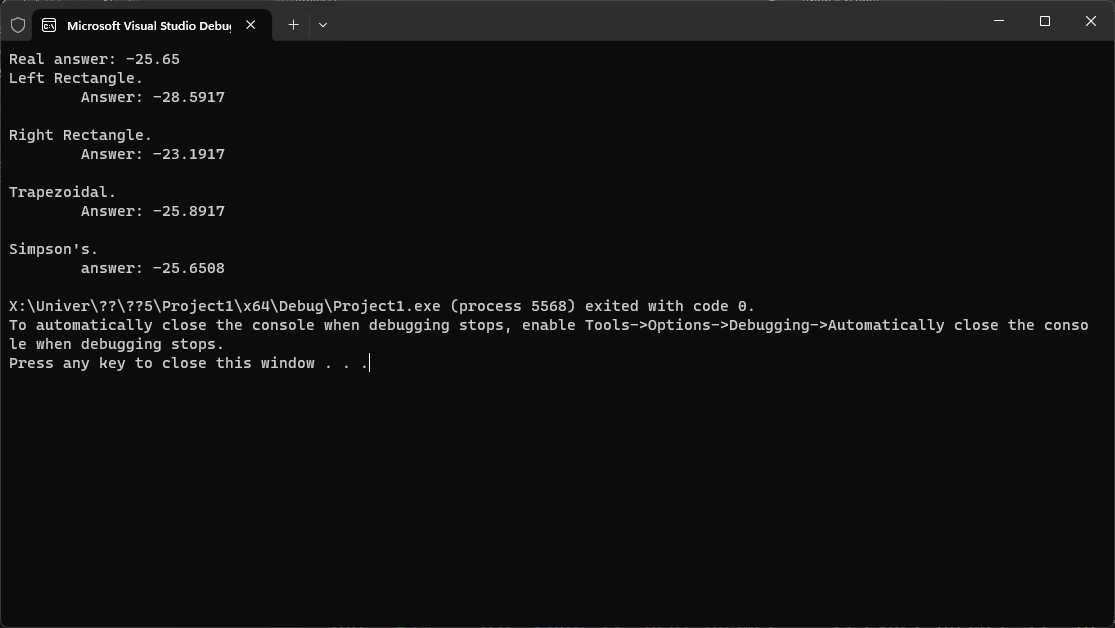
Estimate the absolute and marginal errors for each numerical method and each step h (for n=4 manually, for n=20 by using the program) according to the formulas of absolute limiting errors.
Step n = 4.
Left and right rectangle formula marginal error:
.
Then
Hence
Marginal Error for left rectangle formula:
Absolute error:
For right rectangle formula marginal error:
And absolute error:
Trapezoidal formula error:
.
Then
Hence marginal error
And absolute error
Simpson’s formula error:
Then
Hence marginal error
And absolute error
Step n = 20.
