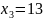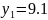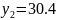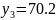- •In the discipline "Numerical methods"
- •The formula:
- •The obtained function is
- •The formula:
- •Substitute the values into the formula:
- •The obtained function is
- •Let's check the continuity of the spline and the first derivative at the interpolation nodes and , that is, at the intersection points of the polynomials.
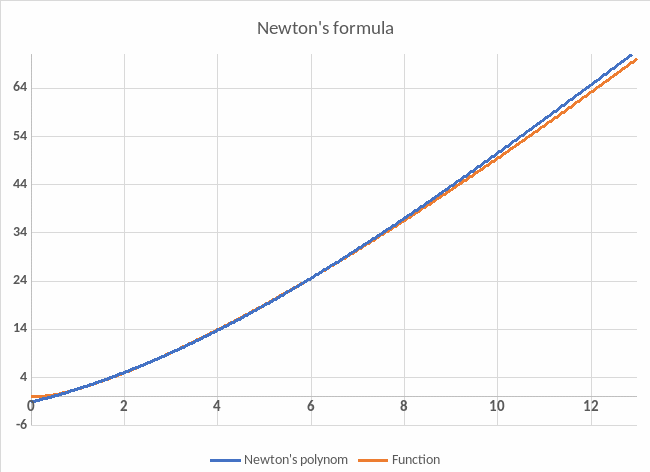
- •Plot the graphs of the given function , the Lagrange polynomial (Newton polynomial) and the interpolating cubic spline in the same coordinate system.
- •Independently set unequally spaced interpolation nodes.
- •Construct interpolation polynomials using Lagrange's interpolation formula, Newton's interpolation formula for unequal interpolation nodes.
- •Plot the graphs of the given function , the Lagrange polynomial and Newton polynomial in the same coordinate system.
Independently set unequally spaced interpolation nodes.
Construct interpolation polynomials using Lagrange's interpolation formula, Newton's interpolation formula for unequal interpolation nodes.
Lagrange's interpolation formula:
Construct a table of 4 unequal interpolation nodes.
x |
|
|
|
|
y = f(x) |
|
|
|
|
Substitute the table values into the formula.

The obtained function is


Newton's interpolation formula for unequal interpolation nodes:
The formula:
 + … +
+ … +
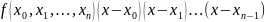
Write the formula for our case of 4 nodes:

Substitute the values into the formula:
x |
|
|
|
|
y = f(x) |
|
|
|
|
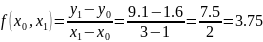
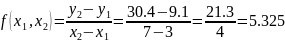
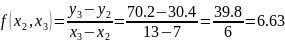


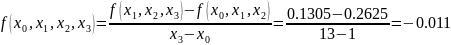

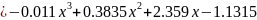
The obtained function is

3.2 Calculate the value of the given function y = f(x), Lagrange polynomial and Newton polynomials at interpolation nodes x = 1, 3, 7, 13 and intermediate points x = 2, 5, 9 on each partial segment of interpolation.
The value of function :
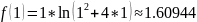
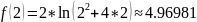
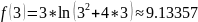
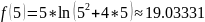

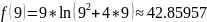
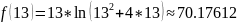
The value of Lagrange’s polynomial
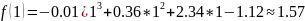
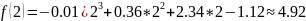




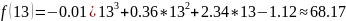
The value of Lagrange’s polynomial
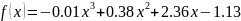
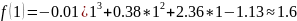
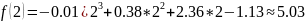
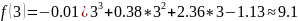
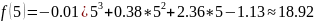
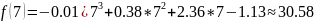
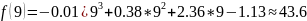

Table for each obtained value.
x |
Function |
Lagrange's |
Newton's |
1 |
1.60944 |
1.57 |
1.6 |
2 |
4.96981 |
4.92 |
5.03 |
3 |
9.13357 |
8.87 |
9.1 |
5 |
19.03331 |
18.33 |
18.92 |
7 |
30.40664 |
29.47 |
30.58 |
9 |
42.85957 |
41.81 |
43.6 |
13 |
70.17612 |
68.17 |
71.8 |
3.3 Calculate the absolute errors. Let Function =
,
Lagrange’s polynomial =
and Newton’s polynomial =
 ,
then Lagrange polynomial errors at the given points are
,
then Lagrange polynomial errors at the given points are
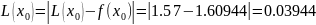
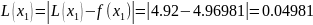
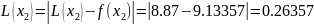
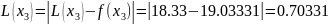

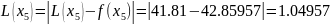

and Newton’s polynomial’s errors

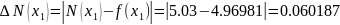

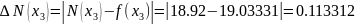
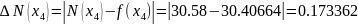

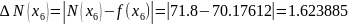
f(x) |
L(x) |
∆L(x) |
N(x) |
∆N(x) |
1.609438 |
1.57 |
0.03944 |
1.6 |
0.009438 |
4.969813 |
4.92 |
0.04981 |
5.03 |
0.060187 |
9.133567 |
8.87 |
0.26357 |
9.1 |
0.033567 |
19.03331 |
18.33 |
0.70331 |
18.92 |
0.113312 |
30.40664 |
29.47 |
0.93664 |
30.58 |
0.173362 |
42.85957 |
41.81 |
1.04957 |
43.6 |
0.740435 |
70.17612 |
68.17 |
2.00612 |
71.8 |
1.623885 |
Plot the graphs of the given function , the Lagrange polynomial and Newton polynomial in the same coordinate system.
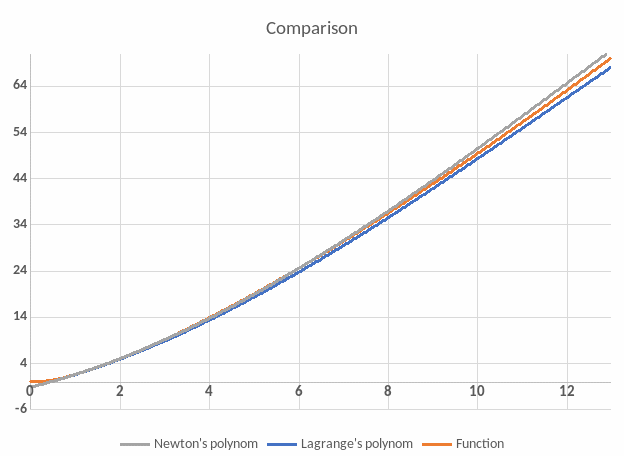
Conclusion: During the work we performed a lot of calculations to interpolation the given function. We first constructed them at equally spaced nodes, using Lagrange’s, Newton’s first and second and spline formulas and then set unequally spaced nodes. All of them gave us appropriate approximate result. But, by finding errors of these polynomials we can conclude several things: 1. Taking equally spaced nodes is surely more precise than taking unequally spaced because the function values begin to range greater and errors between calculation rise, 2. The rounding errors dominate when working with very small values and when taking equally spaced nodes you don’t have to round a lot of values so in the end you obtain that Lagrange’s polynomial equals to Newton’s, they have different formulas but same result, so the errors are as well the same. 3. Finally, considering all the obtained errors and graphs we can say that for equally spaced nodes spline is the most precise option, but as for unequally spaced nodes the Newton’s interpolation is better – the errors are smaller the values are better.