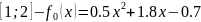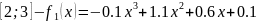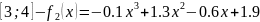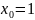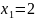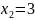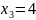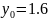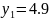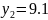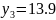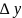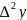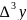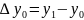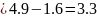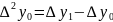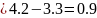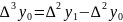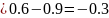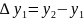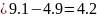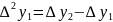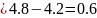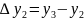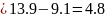- •In the discipline "Numerical methods"
- •The formula:
- •The obtained function is
- •The formula:
- •Substitute the values into the formula:
- •The obtained function is
- •Let's check the continuity of the spline and the first derivative at the interpolation nodes and , that is, at the intersection points of the polynomials.
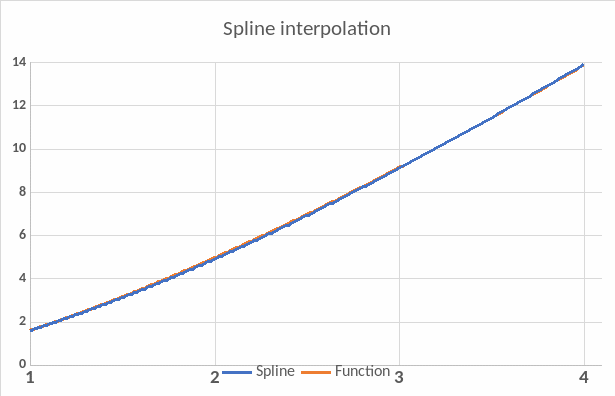
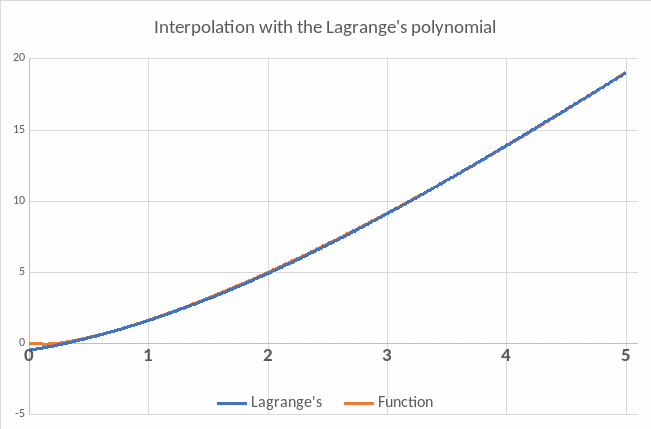
- •Plot the graphs of the given function , the Lagrange polynomial (Newton polynomial) and the interpolating cubic spline in the same coordinate system.
- •Independently set unequally spaced interpolation nodes.
- •Construct interpolation polynomials using Lagrange's interpolation formula, Newton's interpolation formula for unequal interpolation nodes.
- •Plot the graphs of the given function , the Lagrange polynomial and Newton polynomial in the same coordinate system.
MINISTRY OF EDUCATION AND SCIENCE OF UKRAINE
KHARKIV NATIONAL UNIVERSITY OF RADIO ELECTRONICS
Department of ST
Report
on the implementation of laboratory work No. 4
"Interpolations"
In the discipline "Numerical methods"
Complied by student KNT-23-1: Roman, Kravchenko
Kharkiv 2024 |
Accepted: P.E. Sytnikova,
|
Purpose of the work: acquisition of practical skills of interpolation of functions in modeling problems of complex objects and systems. Comparative analysis of methods and ways of solving problems of interpolation of functions.
Variant 11:
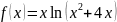
The graph of the function
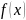 .
.
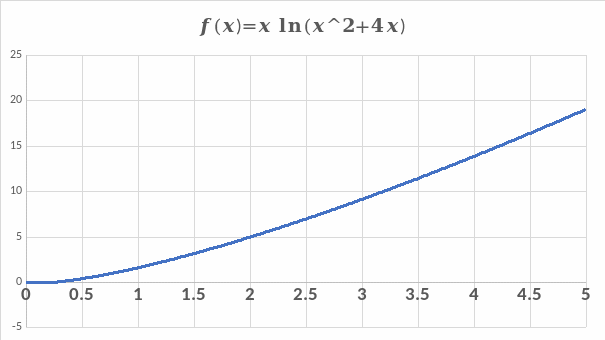
Independently set equidistant interpolation nodes.
Constructed interpolation polynomials using Lagrange's interpolation formula, Newton's first interpolation formula, Newton's second interpolation formula, cubic spline interpolation formula.
Lagrange's interpolation formula:
The formula:
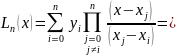
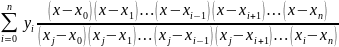
Write down the Lagrange’s formula for our case of 4 nodes:
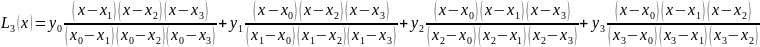
Construct a table of 4 nodes.
x |
|
|
|
|
y = f(x) |
|
|
|
|
Substitute the table values into the formula.
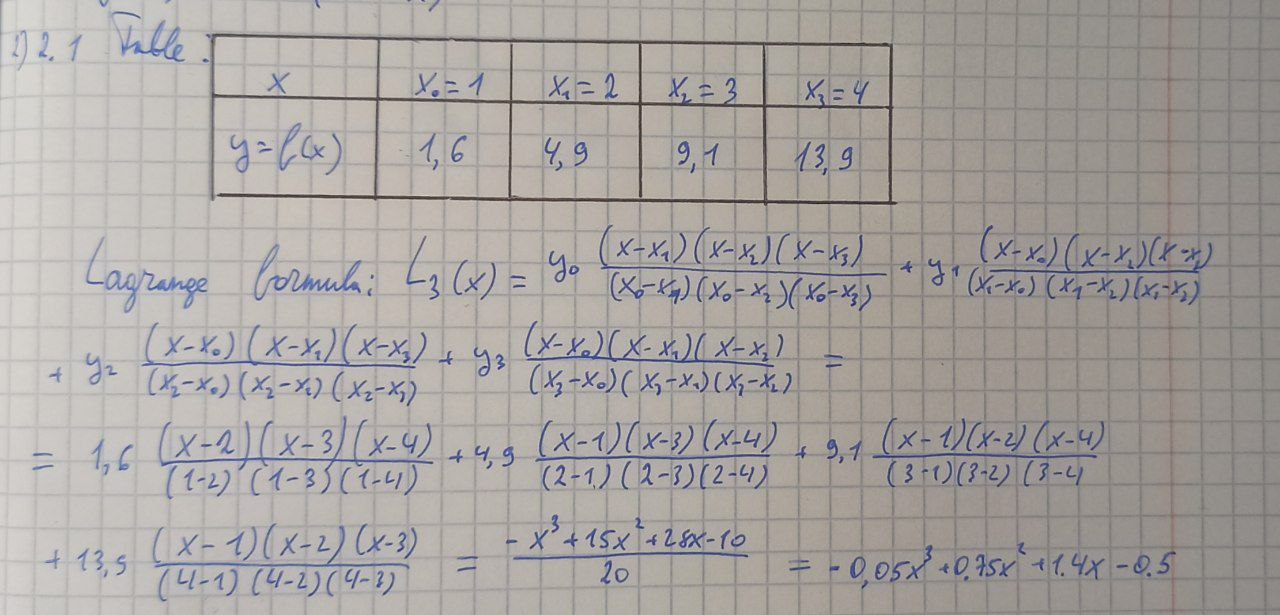
The obtained function is
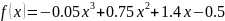
Newton's first interpolation formula:
The formula:
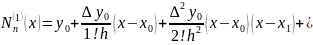
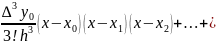
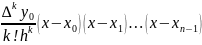
Where
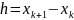
Write the Newton’s first interpolation formula for the case of 4 nodes:
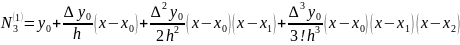
Generate the finite difference table. Where
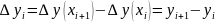
and
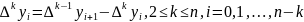
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Substitute the values into the formula:

The obtained function is
Newton's second interpolation formula.
The formula:
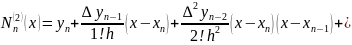
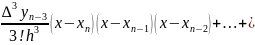
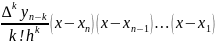
Write the Newton’s second interpolation formula for the case of 4 nodes:
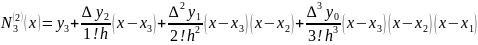
Generate the finite difference table.
x
y
Substitute the values into the formula:

The obtained function is
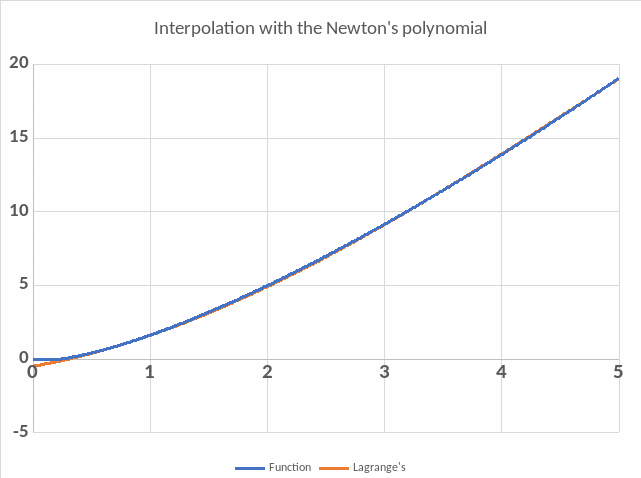
After this step we can notice that using Lagrange’s and Newton’s formulas we obtain the same exact function.
The formula for cubic spline.
If
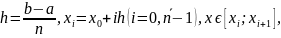 then
cubic spline can be represented by the formula on this interval:
then
cubic spline can be represented by the formula on this interval:
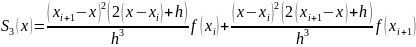
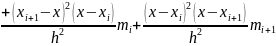
Table of the required values:
x
1
2
3
4
y
1.6
4.9
9.1
13.9
y`
2.8
3.8
4.5
5
Substitute values into the formula:

We now have got three cubic polynomials for each interval: