
- •In the discipline "Numerical methods"
- •Performed the root separation procedure. Found the segments containing one root of the equation.
- •Implemented the procedure for specifying the roots of the equation using the given method.
- •Programs listing and the number of iterations to find each root.
- •A table (graph) of the dependence of the number of approximations on the solution method. Analyze the results.
A table (graph) of the dependence of the number of approximations on the solution method. Analyze the results.
The solving table for bisection method:
k |
a(k) |
b(k) |
f( |
f( |
(a + b)/2 |
f((a+b)/2) |
ε=0.001 |
| - |<2*ε |
x1: |
||||||||
|
-3.0352 |
-1.6352 |
-10.6081 |
0.8424 |
-2.3352 |
-1.9401 |
|
FALSE |
1 |
-2.3352 |
-1.6352 |
-1.9401 |
0.8424 |
-1.9852 |
0.0582 |
|
FALSE |
2 |
-2.3352 |
-1.9852 |
-1.9401 |
0.0582 |
-2.1602 |
-0.7731 |
|
FALSE |
3 |
-2.1602 |
-1.9852 |
-0.7731 |
0.0582 |
-2.0727 |
-0.3175 |
|
FALSE |
4 |
-2.0727 |
-1.9852 |
-0.3175 |
0.0582 |
-2.0289 |
-0.1199 |
|
FALSE |
5 |
-2.0289 |
-1.9852 |
-0.1199 |
0.0582 |
-2.0071 |
-0.0285 |
|
FALSE |
6 |
-2.0071 |
-1.9852 |
-0.0285 |
0.0582 |
-1.9961 |
0.0154 |
|
FALSE |
7 |
-2.0071 |
-1.9961 |
-0.0285 |
0.0154 |
-2.0016 |
-0.0064 |
|
FALSE |
8 |
-2.0016 |
-1.9961 |
-0.0064 |
0.0154 |
-1.9989 |
0.0046 |
|
FALSE |
9 |
-2.0016 |
-1.9989 |
-0.0064 |
0.0046 |
-2.0002 |
-0.0009 |
|
FALSE |
10 |
-2.0002 |
-1.9989 |
-0.0009 |
0.0046 |
-1.9995 |
0.0018 |
|
TRUE |
x1 = -1.9995 |
||||||||
x2: |
||||||||
|
-1.2597 |
0.7685 |
0.6267 |
-6.0296 |
-0.2456 |
-2.9721 |
|
FALSE |
11 |
-1.2597 |
-0.2456 |
0.6267 |
-2.9721 |
-0.7527 |
-0.8492 |
|
FALSE |
12 |
-1.2597 |
-0.7527 |
0.6267 |
-0.8492 |
-1.0062 |
0.0185 |
|
FALSE |
13 |
-1.0062 |
-0.7527 |
0.0185 |
-0.8492 |
-0.8794 |
-0.3890 |
|
FALSE |
14 |
-1.0062 |
-0.8794 |
0.0185 |
-0.3890 |
-0.9428 |
-0.1779 |
|
FALSE |
15 |
-1.0062 |
-0.9428 |
0.0185 |
-0.1779 |
-0.9745 |
-0.0778 |
|
FALSE |
16 |
-1.0062 |
-0.9745 |
0.0185 |
-0.0778 |
-0.9903 |
-0.0291 |
|
FALSE |
17 |
-1.0062 |
-0.9903 |
0.0185 |
-0.0291 |
-0.9983 |
-0.0052 |
|
FALSE |
18 |
-1.0062 |
-0.9983 |
0.0185 |
-0.0052 |
-1.0022 |
0.0067 |
|
FALSE |
19 |
-1.0022 |
-0.9983 |
0.0067 |
-0.0052 |
-1.0003 |
0.0007 |
|
FALSE |
20 |
-1.0003 |
-0.9983 |
0.0007 |
-0.0052 |
-0.9993 |
-0.0022 |
|
TRUE |
x2 = -0.9993 |
||||||||
x3: |
||||||||
|
1.1440 |
3.4194 |
-5.7701 |
33.9969 |
2.2817 |
3.9584 |
|
FALSE |
21 |
1.1440 |
2.2817 |
-5.7701 |
3.9584 |
1.7129 |
-2.8923 |
|
FALSE |
22 |
1.7129 |
2.2817 |
-2.8923 |
3.9584 |
1.9973 |
-0.0326 |
|
FALSE |
23 |
1.9973 |
2.2817 |
-0.0326 |
3.9584 |
2.1395 |
1.8129 |
|
FALSE |
24 |
1.9973 |
2.1395 |
-0.0326 |
1.8129 |
2.0684 |
0.8537 |
|
FALSE |
25 |
1.9973 |
2.0684 |
-0.0326 |
0.8537 |
2.0328 |
0.4016 |
|
FALSE |
26 |
1.9973 |
2.0328 |
-0.0326 |
0.4016 |
2.0151 |
0.1823 |
|
FALSE |
27 |
1.9973 |
2.0151 |
-0.0326 |
0.1823 |
2.0062 |
0.0743 |
|
FALSE |
28 |
1.9973 |
2.0062 |
-0.0326 |
0.0743 |
2.0017 |
0.0207 |
|
FALSE |
29 |
1.9973 |
2.0017 |
-0.0326 |
0.0207 |
1.9995 |
-0.0060 |
|
FALSE |
30 |
1.9995 |
2.0017 |
-0.0060 |
0.0207 |
2.0006 |
0.0073 |
|
FALSE |
31 |
1.9995 |
2.0006 |
-0.0060 |
0.0073 |
2.0001 |
0.0007 |
|
TRUE |
x3 = 2.0001 |
||||||||
The solving table for Newton’s method:
k |
x |
f(x) |
f`(x) |
-f(x) / f`(x) |
x - f(x) / f`(x) |
ε=0.001 |
| |
x1: |
|||||||
|
-3.0352 |
-10.6081 |
17.5667 |
0.6039 |
-2.4313 |
|
|
1 |
-2.4313 |
-2.7356 |
8.8712 |
0.3084 |
-2.1229 |
|
FALSE |
2 |
-2.1229 |
-0.5692 |
5.2747 |
0.1079 |
-2.0150 |
|
FALSE |
3 |
-2.0150 |
-0.0613 |
4.1510 |
0.0148 |
-2.0003 |
|
FALSE |
4 |
-2.0003 |
-0.0011 |
4.0027 |
0.0003 |
-2.0000 |
|
FALSE |
5 |
-2.0000 |
0.0000 |
4.0000 |
0.0000 |
-2.0000 |
|
TRUE |
x1 = -2 |
|||||||
x2: |
|||||||
|
-1.2597 |
0.6267 |
-1.7588 |
0.3564 |
-0.9034 |
|
|
6 |
-0.9034 |
-0.3077 |
-3.3585 |
-0.0916 |
-0.9950 |
|
FALSE |
7 |
-0.9950 |
-0.0151 |
-3.0200 |
-0.0050 |
-1.0000 |
|
FALSE |
8 |
-1.0000 |
0.0000 |
-3.0001 |
0.0000 |
-1.0000 |
|
FALSE |
9 |
-1.0000 |
0.0000 |
-3.0000 |
0.0000 |
-1.0000 |
|
TRUE |
x2 = -1 |
|||||||
x3: |
|||||||
|
3.4194 |
33.9969 |
37.9166 |
-0.8966 |
2.5228 |
|
|
10 |
2.5228 |
8.3301 |
20.1395 |
-0.4136 |
2.1092 |
|
FALSE |
11 |
2.1092 |
1.3952 |
13.5645 |
-0.1029 |
2.0064 |
|
FALSE |
12 |
2.0064 |
0.0764 |
12.0890 |
-0.0063 |
2.0000 |
|
FALSE |
13 |
2.0000 |
0.0003 |
12.0003 |
0.0000 |
2.0000 |
|
FALSE |
14 |
2.0000 |
0.0000 |
12.0000 |
0.0000 |
2.0000 |
|
TRUE |
x3 = 2 |
|||||||
The solving table for combined method:
k |
a(k) |
b(k) |
f( ) |
f( ) |
f`( ) |
b-f(b) / f`(b) |
ε=0.001 |
| - | < 2*ε |
x1: |
||||||||
|
-3.0352 |
-1.6352 |
-10.6081 |
0.8424 |
0.7511 |
-0.1215 |
|
FALSE |
1 |
-2.4313 |
-1.7382 |
-2.7356 |
0.7225 |
1.5874 |
0.5449 |
|
FALSE |
2 |
-2.1229 |
-1.8830 |
-0.5692 |
0.4012 |
2.8710 |
0.8603 |
|
FALSE |
3 |
-2.0150 |
-1.9822 |
-0.0613 |
0.0696 |
3.8229 |
0.9818 |
|
FALSE |
4 |
-2.0003 |
-1.9997 |
-0.0011 |
0.0013 |
3.9967 |
0.9997 |
|
TRUE |
x1 = -1.9999 |
||||||||
x2: |
||||||||
|
-1.2597 |
0.7685 |
0.6267 |
-6.0296 |
-0.6911 |
-7.7244 |
|
FALSE |
5 |
-0.9034 |
-1.0688 |
-0.3077 |
0.1965 |
-2.7108 |
1.0725 |
|
FALSE |
6 |
-0.9950 |
-1.0043 |
-0.0151 |
0.0129 |
-2.9828 |
1.0043 |
|
FALSE |
7 |
-0.9998 |
-1.0001 |
0.0000 |
0.0000 |
-2.9999 |
1.0000 |
|
TRUE |
x2 = -0.9999 |
||||||||
x3: |
||||||||
|
3.4194 |
1.1440 |
33.9969 |
-5.7701 |
2.2140 |
3.6062 |
|
FALSE |
8 |
2.5228 |
1.4741 |
8.3301 |
-4.5200 |
5.4676 |
1.8267 |
|
FALSE |
9 |
2.1092 |
1.8430 |
1.3952 |
-1.7152 |
9.8761 |
1.1737 |
|
FALSE |
10 |
2.0064 |
1.9898 |
0.0764 |
-0.1217 |
11.8575 |
1.0103 |
|
FALSE |
11 |
1.9998 |
2.0001 |
0.0003 |
-0.0005 |
11.9995 |
1.0000 |
|
TRUE |
x3 = 1.9999 |
||||||||
Anylyzing each of these tables we can conclude that combined method is actually the best and the fastest among all these three. First of all, because it required only 11 iterations while the Newton’s and bisection methods needed 14 and 31 respectively. Secondly, Newton’s and combined gave us more accurate results, than bisection did, so we can say that such taks are better solved by the combination of Newton’s and chord methods. It gives more precise and faster result than any other considered methods.

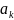 )
)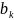 )
)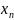 -
-
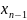 |
< 2ε
|
< 2ε