Programs listing and the number of iterations to find each root.
Code:
#include <vector> #include <iostream> #include <fstream>
#define f(x) value_of_function(x)
//Parameters of cubic parabola constexpr double a = 1.; constexpr double b = 1.; constexpr double c = -4.; constexpr double d = -4.; constexpr double epsilon = 0.001;
//Find the critical point of cubic parabola static std::vector<double> find_the_critical_points() { double temp_a = a * 3.; double temp_b = b * 2.;
//discriminant double D = temp_b * temp_b - 4. * temp_a * c;
if (D > 0) { //find the roots double x1 = (-temp_b + sqrt(D)) / (2. * temp_a); double x2 = (-temp_b - sqrt(D)) / (2. * temp_a);
//return roots in ascending order if (x1 > x2) return { x2,x1 };
return { x1,x2 }; } else if (D == 0) return { -temp_b / (2. * temp_a) };
else { std::cout << "\nThe given function has no critical points.\n" << "The separation of the roots CAN NOT be performed.\n";
exit(EXIT_FAILURE); } }
//Find the value of first derivative of a function static double value_of_first_derivative(const double x) { return 3 * a * pow(x, 2) + 2 * b * x + c; }
//Find second derivative value of a function static double value_of_second_derivative(const double x) { return 6 * a * x + 2 * b; }
//Returns value of function with the specified input static double value_of_function(const double x) { return a * pow(x, 3) + b * pow(x, 2) + c * x + d; }
//Specifies whether function has a root at the interval static bool has_root_at_the_interval(const double left, const double right) { double left_value = value_of_function(left); double right_value = value_of_function(right);
return left_value * right_value < 0; }
//Finds the correct intervals where function has different signs static std::vector<double> find_intervals() { //vector of function critical points const std::vector<double> crit_points = find_the_critical_points();
//points of intervals std::vector<double> points;
//value to increase/decrease points' value double dx = 0.1;
double right_limit; double left_limit;
const int MAX_ITERATIONS = 3000; for (size_t i = 0; i < crit_points.size(); i++) { //set the right limit as a difference between current critical point and dx right_limit = crit_points[i] - dx;
//set the left limit with smaller value as right limit left_limit = right_limit - dx;
//iterate while the function values in current points don't have different signs int j = 0; while (j <= MAX_ITERATIONS) { if (i > 0) { dx = std::abs(left_limit - crit_points[i - 1]) / 2; //the left limit value is too close to the critical_points, the root is more likely absent if (std::abs(left_limits – crit_points[i-1]) < 0.01) break; } left_limit -= dx;
//found two points with different function signs if (f(left_limit) * f(right_limit) < 0) { points.insert(points.end(), { left_limit, right_limit }); break; }
++j; } } //set the rightmost interval(the left limit is bigger than the last critical point) left_limit = crit_points.back() + dx; right_limit = left_limit + dx;
int j = 0; while (j<=MAX_ITERATIONS) { ++right_limit; if (f(left_limit) * f(right_limit) < 0) { points.insert(points.end(), { left_limit, right_limit }); break; }
++j; }
return points; }
//Tells the results of the given method static void result_of_method(std::string const& name, std::vector<double> roots, int iterations) { std::cout << "The " << name << " method" << " required " << iterations << " number of iterations to find all the roots\n" << "The approximate roots are: \n";
for (size_t i = 0; i < roots.size(); i++) std::cout << "x" << i + 1 << " = " << roots[i] << std::endl; std::cout << std::endl; }
//Bisection method to solve cubic equation static void bisection_method() { std::vector<double> roots; std::vector<double> intervals = find_intervals();
int k = 0; for (size_t i = 0; i < intervals.size(); i += 2) { double ak = intervals[i]; double bk = intervals[i + 1]; double ck;
//actually this step is uncessary because in 'find_intervals' we actually perform this check if (!has_root_at_the_interval(ak, bk)) continue;
while (std::abs(ak - bk) >= 2 * epsilon) { ck = (ak + bk) / 2.;
if (f(ak) * f(ck) < 0) bk = ck;
else if (f(bk) * f(ck) < 0) ak = ck;
++k; } roots.emplace_back(ck); } result_of_method("Bisection", roots, k); }
static void newtons_method() { std::vector<double> roots; std::vector<double> intervals = find_intervals();
int k = 0; for (size_t i = 0; i < intervals.size(); i += 2) { if (!has_root_at_the_interval(intervals[i], intervals[i + 1])) continue;
double x0; double x = (intervals[i] + intervals[i + 1]) / 2;
if (value_of_first_derivative(x) * value_of_second_derivative(x) < 0) x = intervals[i]; else x = intervals[i + 1];
do { x0 = x; x = x - (f(x) / value_of_first_derivative(x));
++k; } while (std::abs(x0 - x) >= epsilon); roots.emplace_back(x); } result_of_method("Newton's", roots, k); }
static void combined_method() { std::vector<double> roots; std::vector<double> intervals = find_intervals();
int k = 0; for (size_t i = 0; i < intervals.size(); i += 2) { if (!has_root_at_the_interval(intervals[i], intervals[i + 1])) continue;
double a_k = (intervals[i] + intervals[i + 1]) / 2; double b_k;
if (value_of_first_derivative(a_k) * value_of_second_derivative(a_k) < 0) { a_k = intervals[i]; b_k = intervals[i + 1]; } else { b_k = intervals[i]; a_k = intervals[i + 1]; } while (std::abs(a_k - b_k) > 2 * epsilon) { b_k = b_k - ( f(b_k) * (a_k - b_k) ) / ( f(a_k) - f(b_k) ); a_k = a_k - (f(a_k) / value_of_first_derivative(a_k));
++k; } roots.emplace_back((a_k + b_k) / 2); } result_of_method("combined", roots, k); }
int main() { bisection_method(); newtons_method(); combined_method();
return 1; } |
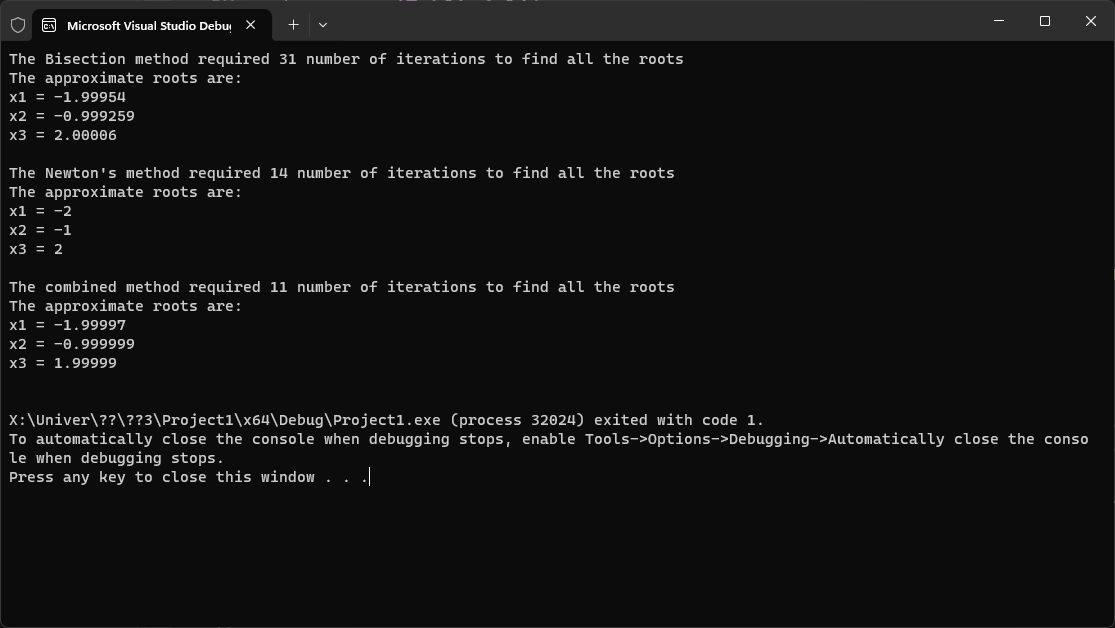
The program’s output:
