
chachshin_lab12
.pdfМИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Кафедра ЛИНС
ОТЧЕТ по лабораторной работе № 12
по дисциплине «Информационные технологии в приборостроении» ТЕМА: « Моделирование переходных процессов
В однородных линиях»
Студент гр. 0584 |
|
Чащин Д. |
|
Преподаватель |
|
Антонюк П.Е |
|
|
|||
|
|
|
|
Санкт-Петербург
2024

Цель работы: В работе исследуются переходные процессы, возникающие при коммутациях в длинных линиях без потерь. Для моделирования процессов используются виртуальные инструменты VI в среде LabVieW.
Вариант схемы соединений линий:
Входными данными являются: U = 100 кВ, L1 = 180 км, L2 = 60 км, L3 = 100
км, L1 = 0 Гн, Zc1 = Zc2 = 350 Ом, Zc3 = 40 Ом, R2 = 150 Ом, С1 = 10 мкФ, v1 = v2 = 3 10 5 км/с, v3 = 1,5 105 км/с, а = 9 км/с, t = 10-3 с.
Рисунок 1 - схема соединения линий
Следует отметить, что длина третьей линии в задании равна 100 км., а на рисунке она удвоена. Это объясняется особенностью представления переменных с помощью ВИ. Как следует из расчета, за время t волновой процесс распространяется вдоль линий так, как указано на рисунке 1. Однако,
скорость распространения волны в линии 3 в два раза меньше, чем в остальных линиях. Поскольку все переменные в компьютере представлены в выборках,
то следует либо удвоить длину 3 линии, либо ввести коэффициент 2 в
уравнение переходных процессов путем замены x на 2x.
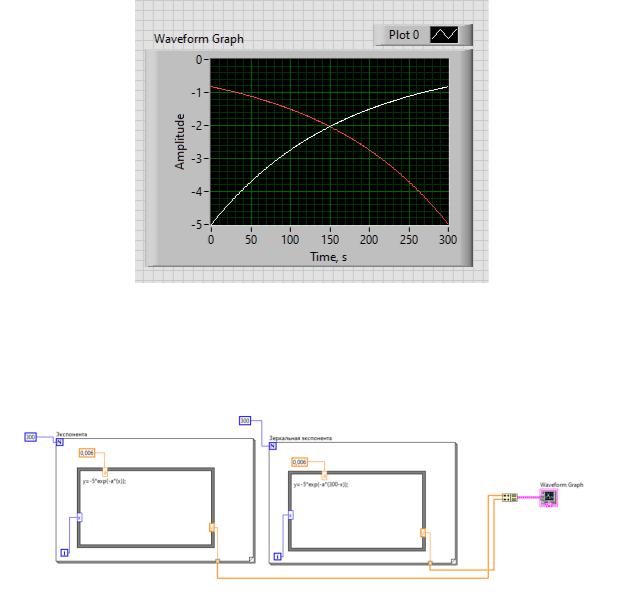
Графическое представление экспоненты с помощью VI:
На рисунке 2 на экране виртуального осциллографа представлен результат моделирования исследуемых процессов - экспонента f(t) = - Aexp( - (t)) (белый цвет) и зеркальная ей кривая: f(t) = - Aexp( - (b - t)) (красный цвет), где t –
текущее значение выборки, b – число выборок (b = 300). По оси абсцисс указаны номера выборки, а по оси ординат дискретные отсчеты значений f(t)
при A = 5.
Рисунок 2 - результат моделирования
Схема работы представлена на рисунке 3:
Рисунок 3 - схема работы

Имитация распространения прямой и обратной волн:
На рисунке 4 а) представлена зависимость тока прямой волны
iп = – Bk exp( x) |
(1) |
где x – расстояние, выраженное в выборках, а константа Bk меняется по закону
Bk = B0 exp(– t) |
(2) |
переменная t использована как параметр и тоже выражена в выборках. Подставив (2) в (1), получим
iп = – B0 exp(– (t – x)) |
(3) |
Если ограничить графики уровнем B0 при x = 0, то для точек B0, 3, 4, мы увидим перемещение экспоненты слева направо, что может имитировать распространение прямой волны (например, тока). Стрелки на рисунке указывают смещение фронта прямой волны.
а) |
б) |
Рисунок 4 - зависимость тока от прямой волны
Для рисунка 4 б) имеем |
|
iо = – Ak exp(– x) |
(4) |
где |
|
Ak = A0 exp(– t) |
(5) |
При условии t = 0, x = x1 и B0 = A0 exp(– x1), где x1 – длина линии в выборках, получим
i0 = – A0 exp(– (t + x)) = – B0 exp(– (t + x - x1). |
(10) |

На уровне B0 и точек B0, 4, 3, мы увидим перемещение экспоненты справа налево, что может имитировать движение обратной волны. Стрелки на рисунке указывают смещение фронта обратной волны.
На рисунках 5 и 6 представлен результат виртуальной имитации прямой
волны.
Рисунок 5 - результат имитации при t=300

Рисунок 6 - результат имитации при t=42,851
Схема работы представлена на рисунке 7:
Рисунок 7 - схема работы
На рисунках 8,9, и 10 приведены результаты виртуальной имитации обратной волны и схема работы.
Рисунок 8 - результат имитации при t=300

Рисунок 9 - результат имитации при t=42,851
Применение VI для анимации прямой и обратной волны
На рисунках 11, 12 и 13 приведены приборная панель и блок диаграмма VI,
позволяющие имитировать движение прямой и обратной прямой волны в 3
линии на рисунке 10:
Рисунок 10 - 3 линия
Результаты имитации (белый увет - прямая волна, серый - обратная):

Рисунок 11 - конечный результат имитации

Рисунок 12 - результат имитации в процессе
