Учебники / 2 курс 1 семестр / Русаленко Науки о Земле

Сельскохозяйственное использование осушенных земель привело к ухудшению качественного состава рек Белорусского Полесья и грун- товых вод. Общая минерализация речных вод на указанной территории возросла в 1,4–1,7 раза. Использование торфа как сырья предусматри- вает его промышленную добычу. Промышленная разработка торфя-

ных месторождений увеличивает скорость выноса углерода с болот в 300–500 раз по сравнению с осушением.

Таким образом, естественные болота очищают атмосферу и грун- товые воды от СО2, а осушенные болота, наоборот, переводят углерод прошлых эпох из торфяных залежей в атмосферу и грунтовые воды. Из этого можно сделать вывод, что современные способы сельскохо-

зяйственного и промышленного использования болот противоречат законам развития нашей планеты и должны быть заменены другими, бо- лее совершенными способами.

Глава 10. ГЕОЛОГИЧЕСКАЯ ДЕЯТЕЛЬНОСТЬ ЛЕДНИКОВ

В конце XVIII – начале XIX в. сформировалась самостоятельная область знаний, названная гляциологией. Гляциология (от лат. glacies – лед) – наука о формах льда на земной поверхности (ледники, снежный покров и др.), о подземных льдах, их строении, составе, физических свойствах, происхождении и развитии, геологической и геоморфоло- гической деятельности и о географическом распространении. Основ- ными объектами гляциологии, имеющими наибольшее распростране- ние на Земле, являются подземные льды, снежный покров и ледники.

Подземными льдами называют все виды льда в мерзлых породах вне зависимости от их образования, размеров и условий залегания.

На огромной территории северного полушария поверхностные слои почв и грунтов подвергаются сезонному промерзанию зимой и оттаиванию в весенне-летнее время. Этот верхний слой периодического промерзания и оттаивания называется деятельным слоем. Ниже него на обширных про-

странствах Евразии и Северной Америки развиты многолетние мерзлые горные породы (вечная мерзлота). Характер пространственного распро-

странения вечной мерзлоты определяется условиями теплообмена на поверхности Земли. Южная граница распространения вечной мерзлоты совпадает с границей, где горные породы имеют нулевую температуру

на подошве слоя годовых колебаний. При движении с юга на север круп- ность массивов вечной мерзлоты увеличивается, одновременно воз- растает и ее мощность от 5–15 до 700–900 м и более. Рекордной мощ- ности многолетняя мерзлота достигает у северных берегов реки Ви- люй (Сибирь), где она простирается на глубину свыше 1370 м.

Мерзлые горные породы являются прочным основанием для раз- личных сооружений. Однако они весьма чувствительны к изменению температур. Обычно сооружения и линейные коммуникации (дороги, газо- и нефтепроводы) являются источником тепла, вследствие чего под ними мерзлые породы протаивают, что приводит к деформациям строительных объектов. Аналогичные явления могут проявляться при глобальном повышении температуры на Земле.

В умеренных широтах при температуре ниже 0°С атмосферные осадки выпадают преимущественно в виде снега, образуя снежный покров. Как временное, сезонное явление снежный покров образуется ежегодно на территории от 47 до 99 млн. км2.

На Земле имеются районы, где снежный покров сохраняется в тече- ние всего года. Их называют районами вечного снега. Условная линия на земной поверхности, выше которой накопление твердых атмосферных осадков преобладает над их таянием и испарением, называется снеговой границей (линией). Высота ее в полярных областях находится на уровне моря, а в экваториальных – на несколько километров выше уровня моря. Так, в умеренном поясе (северо-западные склоны Кавказа) она находит- ся на высоте 2500 м, а на юго-восточных склонах поднимается до 3800 м. Над экватором она соответствует высоте около 6000 м. Например, по- стоянный ледник 5-километровой ширины находится на вершине вул- кана Килиманджаро (Восточная Африка, Танзания) при высоте вулкана 5895 м и расстоянии до экватора 300 км (около 3° южной широты). Сне- говая линия не остается все время на одном уровне. При похолодании и увеличении влажности климата на Земле она перемещается вниз, а при потеплении и уменьшении влажности – вверх.

Под воздействием различных причин накопившиеся на склонах гор снеговые массы могут обрушиваться, образуя снежные обвалы и ла- вины, иногда с катастрофическими последствиями.

Расположенный выше снеговой границы снег уплотняется, смер-

зается в крупные ледяные кристаллы и в таком виде его называют фирном. Под воздействием возрастающего давления всей толщи снежного покрова фирн уплотняется, из него вытесняется воздух

Днепровское оледенение, или рисское первое оледенение, длилось

70 тыс. лет (320–250 тыс. лет назад). Ледник покрывал всю террито- рию Беларуси и распространился далеко на юг за ее пределы. Отложе- ния, сформировавшиеся во время данного оледенения, на юге и в цен- тре Беларуси часто выходят на дневную поверхность и имеют мощ- ность от 5 до 30 м, а в некоторых случаях до 100 м и более.

Сожское оледенение, или рисское второе, или московское, дли-

тельностью 110 тыс. лет (220–110 тыс. лет назад) охватило северную часть Беларуси до границы Пружаны – Береза – Ивацевичи – Баранови- чи – Выгоновское озеро – Солигорск – Любань – Глуск – Бобруйск – Рогачев – Краснополье – Климовичи. На низинах мощность отложе- ний этого оледенения достигает 10–25 м, а в пределах Ошмянской и Минской возвышенностей – до 60–135 м.

Поозерское оледенение (валдайское) – это последнее оледенение на территории Беларуси, длилось около 85 тыс. лет (95–10 тыс. лет назад). Площадь, занятая в это время ледником, примерно совпадает с территорией Белорусского Поозерья. Граница наибольшего развития льдов (18–17 тыс. лет назад) проходила по северным склонам Грод- ненской возвышенности, по линии Островец – Докшицы – Лепель – Орша и дальше вдоль Днепра. Мощность отложений этого оледенения в среднем 25–30 м, доходит в некоторых местах до 70 м.

Хотя ныне на Земле стало значительно теплее, чем 15–20 тыс. лет назад, и мы живем сейчас в очередном межледниковье, весьма обшир- ная территория суши покрыта ледниками. Накопленные за последние десятилетия знания о современных ледниках являются ключом к рас- познаванию прошлых эпох оледенения, и одновременно эти знания не- обходимы для экстраполяции климата хотя бы на ближайшее будущее.

Методы распознавания оледенений, которыми пользуются ученые при исследовании этого явления, весьма разнообразны. Признаками оледенений являются: низкая температура, особенно летом, измене- ния в составе флоры и фауны, низкий уровень Мирового океана и лед- никовые отложения.

Динамика средней температуры на Земле за последние 600 тыс. лет показывает периодичность чередования холодных и теплых перио- дов, а закономерный ритм последовательности гляциалей и антигля- циалей наводит на мысль о существовании какого-то фактора, который изменяется сходным образом. Насколько сейчас известно науке, един-

ственное наиболее приемлемое объяснение этого явления состоит

втом, что эта причина находится вне Земли и, вероятно, связана с коле- баниями количества энергии, получаемой Землей от Солнца, хотя дос- товерно причины оледенений до сих пор не установлены.

Впериоды оледенений расположенная на материках многометро- вая толща льда создает огромную нагрузку на земную кору. Так, по-

верхностные породы в центре Гренландии в наши дни массой лежащей на них ледяной шапки опущены вниз до уровня моря. В Скандинавии и

вдругих районах с толстым ледяным покровом во время максимума накопления льда в период последнего ледниковья земная кора находи- лась под особенно большим давлением.

По мере отступления льда во время нынешнего межледниковья земная кора начала подниматься. Процесс этот происходит медленно и

внекоторых местах продолжается и поныне. Установлено, что земная кора в центральной части Скандинавии, являющейся центром оледене- ния Северной Европы, за последние 10 тыс. лет поднялась на 100 м и продолжает подниматься.

Ледниковые отложения. При движении ледники выполняют ог- ромную геологическую работу, следы которой из-за объемности и

масштабности сохраняются в течение длительного геологического времени. Эти следы являются индикаторами оледенений.

Впериоды усиления оледенений ледники медленно продвигаются во все стороны из регионов с максимальной толщиной ледяного по- крова, соскребают по пути движения всю существующую почву и даже часть коренных горных пород. Перемещая с собой различный обло- мочный материал, они, кроме того, действуют подобно гигантским ли- стам наждачной бумаги, протягиваемым по местности, сглаживая ре- льеф в одних местах и образуя его новые формы в других. При этом более мягкие горные породы сдираются и уносятся, а более твердые остаются на месте. Царапины и штрихи, оставшиеся после такой обра- ботки, видны на обнаженных поверхностях твердых горных пород и в наши дни. Иногда они протягиваются на сотни километров, указывая

направление перемещения льда и территории с наибольшей толщиной ледяного покрова, с которых началось оледенение.

При наступлении межледниковья, когда льды отступают (начинают таять), они оставляют после себя весь передвигаемый материал и об- разуются ледниковые отложения. Ледниковые отложения – это боль- шая группа отложений, возникающая в результате деятельности ледни- ков и талых ледниковых вод. Включают различные типы морен,

флювиогляциальные (водно-ледниковые), озерно-ледниковые отложе- ния и др. По характеру обломочного материала выделяют валунную глину (тиль), варвит, галечники, пески, супеси, суглинки и др.

Морена – это отложения, накопленные непосредственно ледника- ми при их движении и выпахивании ложа. Главные признаки морен – неоднородность состава, неотсортированность обломочного матери- ала и отсутствие слоистости. Обломочный материал может быть пред- ставлен тонкими глинами, суглинками, супесями, песком, гравием, галь- кой и валунами, достигающими размеров до 2–3 м. Иногда в составе морен встречаются крупные отторженцы – глыбы коренных пород, ото- рванные от первоначальных месторождений. В зависимости от места, которое занимает переносимый материал по отношению к леднику, раз- личают несколько типов морен: поверхностную, внутреннюю, донную, боковую, конечную и основную.

Поверхностная морена – грубообломочный материал, падающий на поверхность льда со склонов и переносимый ледником. Внутренняя морена – обломки горных пород, находящиеся в толще льда; про-

никают в толщу льда по трещинам или в результате протаивания льда под обломочным материалом, который нагревается солнечными луча- ми. Донная морена состоит из материала, захватываемого ледником в его ложе, а также поступающего под толщу льда с боков ледника и его поверхности. Боковая морена – обломочный материал, захватываемый со склонов долины краем ледника. При отступлении (таянии) ледника образуются основные морены за счет обломочного материала, пере- носимого ледником и составляющего при его движении поверхност- ную, внутреннюю, боковую и донную морены.

Конечные морены – обломочный материал, перемещаемый впере- ди ледника. После отступления ледника конечные морены представляют собой большие длинные валы, гряды или холмы, которые чередуются с ложбинообразными понижениями, занятыми речками, озерами и обра- зовавшимися впоследствии болотами. Конечные морены указывают на места остановки ледника. Наличие на территории нескольких гряд ко- нечных морен свидетельствует о неоднократных остановках ледника. Такие признаки характерны для территории Беларуси.

Отложения ледниковых водных потоков называют водно-ледни-

ковыми или флювиогляциальными (от лат. fluvius – река). В резуль-

тате таяния льда образуются надледниковые и подледниковые вод- ные потоки, которые перерабатывают, перемещают и сортируют как

основную, так и конечную морены. Весь размытый материал выно- сится за пределы ледника, и там где скорость водных потоков умень- шается незначительно, откладывается грубо- и крупнообломочный материал, далее – мелкий песчаный, затем глинистый. Образуются осадки, аналогичные современным речным отложениям. Так перед ледником возникают обширные зандровые поля, сложенные песча- но-глинистыми и песчаными отложениями.

Разновидностью флювиогляциальных отложений являются озеёр- но-ледниковые отложения. Это мелкозернистые осадки, накопивши- еся на дне приледниковых озер. Часто они имеют ленточное строение и состоят из чередующихся слоев песка и глины. Такое строение яви- лось следствием неодновременного выпадения песка и глины из при- носимой в озера ледниковой мути. Песок из поступивших в озеро та- лых вод выпадал быстро, а глинистые частицы длительное время на- ходились во взвешенном состоянии и осаждались лишь зимой, после образования на озере ледяного покрова, когда песчаный материал уже не поступал. Таким образом на протяжении года возникало два слоя (песка и глины), образующих ленту. Такие ленточные глины называют- ся варвитом. Прослои варвита обнаружены на территории Канады в древних горных породах, имеющих возраст 2,3 млрд. лет. Ледниковые

осадки приблизительно такого же возраста обнаружены и в других местах, что указывает на глобальный характер оледенения в начале протерозоя.

Предполагается, что при последнем оледенении образовались от- ложения лёсса, покрывающие иногда огромные территории суши мощ- ным слоем до десятков метров и более. По-видимому, этот уплотнен- ный временем тонкозернистый осадок образовался в период наиболь- шего похолодания. Во время оледенений внутренние части континен- тов, расположенные в средних и даже низких широтах, т. е. за предела- ми ледяного покрова, были холоднее и более безводны, чем сейчас, а во многих случаях гораздо беднее растительностью. Это способство- вало развитию ветровой эрозии, при которой перемещались и отлага- лись в определенных местах пылеватые частицы, образуя лёссовые отложения.

Следует отметить, что последнее наступление ледников достигло своего максимума всего лишь около 20–18 тыс. лет назад. В то время льды покрывали Скандинавию, Северную Европу, отдельные части Северной России, большую часть Великобритании и простирались

южнее Великих озер в Северной Америке. Почти треть всей совре- менной суши была под покровом льда. Такие же условия могут насту- пить в не слишком отдаленном будущем, так как, если судить по про- шлому, наш современный теплый период скоро может закончиться. Тем не менее, поскольку мы точно не знаем, что именно вызывает оледе- нение, эта возможность все еще остается в значительной степени умо- зрительной.

Глава 11. ОСНОВЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ГИДРОМЕТЕОРОЛОГИЧЕСКИХ НАБЛЮДЕНИЙ

11.1. Статистические и вариационные ряды

Гидрометеорологические наблюдения проводятся с целью по- лучения величин различных процессов, имеющих отношение как к метеорологическому, так и к гидрологическому режиму (осадки, снежный покров, испарение, уровень и расход воды в водных объек- тах и др.).

Гидрометеорологические величины весьма изменчивы, посколь- ку обусловливаются многими факторами. Так, высота снежного покрова зависит от количества выпавших атмосферных осадков (снега), харак- тера растительности (поле, лес), рельефа, ветра и др. Уровень и расход воды в реке также определяются рядом факторов.

Несмотря на изменчивость гидрометеорологических величин, которая проявляется как в пространстве, так и во времени, для ре-

шения практических задач необходимо знать значение той или иной величины (среднее, иногда максимальное или минимальное и т. д.). Например, при строительстве плотины на реке необходимо иметь данные о максимальных уровнях и расходах воды и, наоборот, для водоснабжения – их минимальные значения. Необходимые данные можно получить, используя методы математической статистики.

Математическая статистика – наука о математических мето-

дах систематизации и последующего использования полученных ста- тистических данных для научных и практических выводов.

Для статистической обработки необходимо иметь ряд наблюдений, включающий определенное их количество. Чем больше количество

наблюдений, тем точнее будет охарактеризована та или иная гидроме- теорологическая величина. Однако с увеличением количества наблю- дений увеличиваются затраты на их проведение.

В некоторых случаях количество наблюдений ограничено по тех- ническим причинам (например, сведения об уровне воды в реке могут быть получены только за период после организации водомерного по- ста). Тем не менее, оказывается, что по ограниченному количеству на- блюдений, применяя методы математической статистики, можно полу- чить вполне приемлемые выводы для решения практических задач.

Как известно, величины бывают постоянные и переменные. Напри- мер, отношение длины окружности к диаметру есть величина постоян- ная (π ≈3,1416). Поэтому отпадает необходимость в определении это- го отношения всякий раз, когда в этом возникает потребность.

Однако встречающиеся на практике гидрометеорологические ве- личины принимают неодинаковые численные значения у различных чле- нов совокупности. Поэтому возникает необходимость в изучении их изменяемости. Это изучение начинается с проведения соответствую- щих наблюдений, обследований.

Допустим, имеется определенное количество наблюдений за ка- кой-либо переменной гидрометеорологической величиной. В целом данный ряд наблюдений называется совокупностью, а каждое из на- блюдений является членом совокупности. Обозначим данную гидро- метеорологическую величину через x (другую при необходимости можно обозначить через y, третью – через z и т. д.). Количество на- блюдений обозначим через n. Например, имеем хронологический ряд наблюдений за уровнем воды в реке в течение года, т. е. n = 365. Этот ряд называется статистическим рядом xi, т. е. объединяющим значе- ния переменной величины от x1 до xi. В примере с уровнем воды в реке это выглядит следующим образом: x1 (уровень воды за 1 января),

x2 (то же за 2 января), …, x364 (то же за 30 декабря) и x365 (за 31 декабря).

В статистическом ряду интересующая нас величина меняется от одного члена совокупности к другому, или варьирует, т. е. варьирование есть изменяемость величины у отдельных членов совокуп- ности. Если бы не было этого варьирования и величина имела одно и то же значение у всех членов совокупности (например, если бы уровень воды в реке за каждый день был один и тот же), то не было

бы нужды в проведении наблюдений и в последующем изучении полученных данных.

Значения величины у отдельных членов совокупности называются вариантами. В примере с уровнем воды имеем 365 вариантов.

Статистический ряд, он же ряд варьирующих величин, можно упо- рядочить, т. е. расположить варианты в порядке убывания их значений (или возрастания). Такое упорядочение ряда, т. е. расположение вари- антов в порядке убывания или возрастания их значений, называется ран-

жированием ряда.

После ранжирования нетрудно заметить, что варианты с одинако- вым значением встречаются одни редко, другие часто. Числа, которые характеризуют, сколько раз повторяется каждое значение величины у членов данной совокупности, называются частотами и обозначают- ся m. Сумма всех частот равна объему выборки, т. е. числу членов со- вокупности (Σm = n). В результате такой обработки наблюдений полу- чаем так называемый вариационный ряд. Следовательно, вариационным рядом называется такой ряд данных, в котором указаны возмож- ные значения варьирующей величины в порядке убывания или возрас- тания и соответствующие им частоты.

Гидрометеорологические исследования начинаются обычно со сбора обширного цифрового материала, понимание которого облегчается систе- матизацией и представлением исходных данных в виде таблиц и графиков.

Допустим, что в результате измерения высоты снежного покрова в 100 точках получены данные, составляющие статистический ряд сn = 100:

В таком виде ряд мало приспособлен, чтобы характеризовать вы- соту снежного покрова. Поэтому необходимо сгруппировать значения x1, x2, …, xn в k групп с интервалом каждой группы i. Ориентировочно число групп равно корню квадратному из объема совокупности, кото- рое, однако, должно быть не меньше 5 и не больше 20.

Величину интервала групп определяют по соотношению

где xmax – максимальное значение переменной величины в статистическом ряду; xmin –минимальноезначение; R –размах варьирования; k –числогрупп.

Для примера со снежным покровом целесообразно взять семь групп. В этом случае величина интервала будет равна целому числу:

і= R / k = (115 – 45) / 7 = 10 см. При выборке границ групп следует обращать внимание на то, чтобы верхняя граница группы была меньше на цену деления, чем нижняя граница прилегающей соседней группы, т. е. на единицу измерения (в нашем случае на 1 см).

Группировка осуществляется в такой последовательности: 1) опре- деляется размах варьирования результатов измерения, т. е. разность между

наибольшим и наименьшим значением ряда измерений (R = xmax – xmin); 2) устанавливается число групп k и размер интервала группировки

і= R / k; 3) подготавливается макет таблицы сгруппированного распре- деления частот результатов измерений. В первой колонке таблицы запи- сываются группы (интервал группировки), а во второй – число результа- тов измерений, входящих в данный интервал, т. е. частота m (табл. 6).

Таблица 6

Сгруппированное распределение частот по данным измерения высоты снежного покрова в 100 точках

Указанный в таблице ряд пар чисел составляет эмпирическое рас- пределение частот, т. е. распределение частот m по значениям xi. Сум- ма частот равна объему совокупности (Σm = n = 100).

В результате такой обработки материалов наблюдений статистичес- кий ряд преобразуется в вариационный.

11.2.Кривые распределения, их характерные точки

истатистические параметры

Визуальное (от лат. visualis – зрительный, видимый) представле- ние о распределении частот становится еще более наглядным при гра- фическом изображении данных. Этот способ очень удобен, так как по- зволяет сразу охватить важнейшие черты и закономерности распреде- ления наблюдений. Графическое изображение вариационного ряда на-

зывается кривой распределения или вариационной кривой.

Для построения кривойраспределения на горизонтальной линии (оси абсцисс) наносят значения интервала группировки, а по вертикали (оси ординат) – численности этих значений, или частоту m. Масштаб в обоих направлениях следует выбирать такой, чтобы весь график имел удобную и легко обозримую форму. Для выбора соотношения между масштаба-

ми на оси абсцисс и оси ординат при построении графика целесообразно руководствоваться правилом «золотого сечения», согласно которому высота графика должна относиться к его ширине примерно как 5 : 8, т. е. ширина графика должна быть больше его высоты примерно в 1,6 раза.

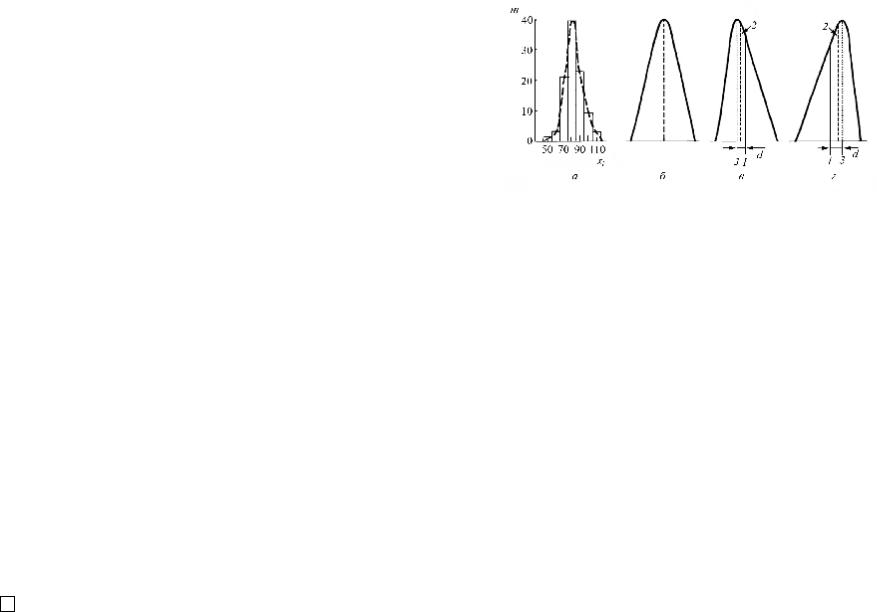
Ступенчатый график в виде столбиков, имеющих высоту, пропор- циональную частотам, а ширину, равную интервалам классов, называ- ется гистограммой, из которой легко получить полигон – кривую рас- пределения, соединив линией средние значения группы (рис. 48).

Обычно в любом ряду переменных величин в выделенных интер- валах наиболее часто будут повторяться величины, группирующиеся около среднего значения всего ряда. Чем ближе к концам ряда, тем меньше число случаев появления рассматриваемой величины в пре- делах интервалов, на которые разбит вариационный ряд при построении кривой распределения. Поэтому кривая распределения в общем слу- чае имеет следующий вид: начинаясь от малых значений повторяемос- ти или нуля, она плавно поднимается до максимума, затем снова опус- кается до весьма малых значений или нуля.

На кривой распределения выделяются три характерные точки: 1) центр распределения; 2) медиана; 3) мода.

Центр распределения соответствует среднему арифметическому ряда. Для ряда величин xi среднее арифметическое определяется по

формуле

Рис. 48. Распределение переменных величин:

а – гистограмма; б – симметричная кивая распределения; в – кривая распределения с положительной асимметрией; г – кривая распределения с отрицательной асимметрией; 1 – среднее арифметическое; 2 – медиана; 3 – мода;

d – радиус асимметрии

Ордината, проходящая через центр распределения, называется цен-

тральной.

Медиана (Ме) – значение переменной величины, которое соответ- ствует середине вариационного ряда. Иными словами, медианой явля- ется вариант, который делит совокупность на две равные по объему части; до медианы и после нее имеется одинаковое число членов со- вокупности. Ордината, проходящая через медиану, делит всю площадь кривой распределения пополам.

Мода (Мо) – значение наиболее часто встречающегося варианта в вариационном ряду. Обычно мода расположена в группе, имеющей максимальную частоту. Ордината, проходящая через моду, называется модальной.

Кривые распределения бывают симметричные и асимметричные. Кривая называется симметричной, если центр распределения, медиа- на и мода совпадают, т. е. все эти три точки имеют общую ординату, которая называется осью симметрии.

Асимметричные распределения – это распределения, у которых частоты вариантов, находящихся по одну сторону от наибольшей час- тоты, больше (или меньше) частот, равноудаленных относительно наи- большей частоты. Степень асимметрии кривой распределения характе-

ризуется расстоянием по оси абсцисс между центральной и модальной

ординатами. Это расстояние называется радиусом асимметрии d. Со-

ответственно асимметричным распределениям кривые распределения бывают с положительной (правосторонней) и отрицательной (левосто- ронней) асимметрией.

Положительная (правосторонняя) асимметрия характеризуется тем, что середина ряда сдвинута вправо от вершины распределения, т. е. частоты сначала быстро возрастают, а достигнув наибольшего зна- чения, в дальнейшем убывают значительно медленнее. При положи- тельной асимметрии центральная ордината расположена правее модаль- ной ординаты.

При отрицательной (левосторонней) асимметрии частоты сна-

чала медленно возрастают, а затем, достигнув наибольшего значения, очень быстро убывают. Поэтому середина ряда сдвинута влево от ва- рианта с наибольшей частотой, т. е. центральная ордината находится левее модальной ординаты.

Кривые распределения могут отличаться друг от друга центрами распределения, мерой рассеивания переменных величин и асимметри- ей. Эти отличительные особенности кривых распределения устанавли- ваются посредством определения основных параметров, к которым относятся среднее арифметическое ряда, коэффициент вариации и ко- эффициент асимметрии. Среднее арифметическое является показате- лем центра распределения. Коэффициент вариации характеризует меру рассеивания переменных величин. Коэффициент асимметрии является показателем симметричности кривой распределения.

Среднее арифметическое значение переменной величины, опреде- ляемое по формуле (53), не дает представления об изменчивости пере- менных величин. Простейшим измерителем изменчивости (или вариа- ции) является размах вариации R, т. е. разность междунаибольшим и наи- меньшим вариантами в вариационном ряду. В примере по высоте снеж- ного покрова R = 115 – 45 = 70 см. Размах вариаций вычисляется только по крайним значениям переменной величины. Остальные во внимание не принимаются. Если к этому добавить, что на крайние варианты могут влиять причины случайного характера (камень, пень и т. д.), то можно заключить, что размах вариации является весьма приближенной характе- ристикой рассеивания, или варьирования, переменной величины.

Часто возникает необходимость сравнения рассеивания различных рядов. Однако сравниваемые ряды могут отличаться средними ариф-

метическими или же последние могут иметь разную размерность

(например, при сопоставлении статистических рядов по высоте снеж- ного покрова в сантиметрах и количества атмосферных осадков в мил- лиметрах). Поэтому сопоставление рассеивания осуществляется с по- мощью коэффициентов вариации.

Коэффициент вариации (Сv), являясь мерой изменчивости той или иной переменной величины, вычисляется для коротких рядов (n ≤ 30)

по формуле

где ki = xi / – модульный коэффициент переменной величины. Аналогично для рядов с n > 30 имеем

Коэффициент вариации, или коэффициент изменчивости, является

безразмерной характеристикой ряда и может выражаться в процентах умножением его на 100. При этом изменчивость считается незначи- тельной, если коэффициент вариации не превышает 10%; средней, если он выше 10%, но менее 20%; значительной, если коэффициент вариа- ции более 20%.

Важной характеристикой вариационного ряда является его симмет- ричность. Предварительное суждение о симметричности ряда можно получить по его графику (кривой распределения или гистограмме). Для характеристики симметричности ряда вычисляется коэффициент асимметрии Сs:

Для вычисления коэффициента асимметрии обычно требуется длин- ный ряд наблюдений (n > 100). При отсутствии такого ряда, что до- вольно часто имеет место при гидрометеорологических исследовани- ях, при установлении коэффициента асимметрии пользуются кривыми вероятности превышения, имеющими жесткое соотношение между ко- эффициентом асимметрии Сs и коэффициентом вариации Сv. Так, соглас- но требованиям СН 435–72, это соотношение может определяться

по рекам-аналогам или приниматься в зависимости от географической широты. Например, для большинства равнинных рек, в том числе и на территории Беларуси, коэффициент асимметрии равен двойному значе- нию коэффициента вариации (Сs = 2Cv).

11.3. Эмпирические и теоретические кривые обеспеченности

По кривым распределения можно определить частоту, или вероят- ность, появления переменной величины в заданном интервале. В прак- тике гидрологических исследований задачи чаще ставятся иначе. Не- обходимо определить частоту, или вероятность, появления исследуе- мой переменной, бульшей или равной заданному значению. Такие зада- чи решаются на основе кривых обеспеченности. Кривые обеспечен- ности бывают эмпирическими и теоретическими.

Эмпирическая (от греч. empeiria – опыт) кривая – это кривая, для построения которой используются данные фактических наблюдений. Эмпирические кривые обеспеченности строятся по эмпирическим кри- вым распределения и представляют собой суммарные значения часто-

ты появления переменной начиная от максимального до наименьшего значения переменной в ряду наблюдений.

Эмпирические кривые обеспеченности могут быть построены дву- мя способами. Для случаев с длинными рядами (n > 100) построение эмпирической кривой обеспеченности производится следующим об- разом. Из ряда переменной величины выбираются ее максимальное и минимальное значения и вычисляется размах (амплитуда) изменения переменной R = xmax – xmin. Полученную амплитуду разбивают на интер- валы, или группы. Число интервалов назначается в зависимости от объема материала и от амплитуды. Обычно назначается порядка 15–20 интерва- лов. Границы интервалов записываются, начиная от максимального зна- чения переменной.

Далее подсчитывается число случаев попадания переменной в каждый интервал. Очевидно, что сумма числа случаев по всем интер- валам равна общей сумме вариантов. Составленная таким образом таблица дает распределение абсолютных частот и называется табли- цей эмпирического распределения. Выражая абсолютные частоты в процентах от общей суммы вариантов, получаем распределение от- носительных частот.

Последовательно суммируя абсолютные и относительные частоты по интервалам, начиная от максимального интервала, получаем абсолют- ные и относительные накопленные частоты, или обеспеченности.

Эмпирические распределения и обеспеченности можно предста- вить в виде графиков. При их построении на оси ординат обычно откла- дываются интервалы переменной, а по оси абсцисс – частота или ее выражение в процентах.

График распределения частот строится в виде прямоугольников и называется, как было отмечено, гистограммой. Табличное и графичес- кое изображение частот называется эмпирическим распределением.

График нарастания частот строится в виде плавной линии. Значения накопленных частот в гидрологии обычно относятся к нижним грани- цам интервалов. Такая кривая показывает повторяемость переменной выше или ниже заданного значения и в относительном выражении – обеспеченность переменных, бульших или равных заданному значению.

Табличное и графическое изображение нарастания частот называ-

ется эмпирической кривой обеспеченности.

Порядок обработки длинных рядов наблюдений (n > 100) и по- строения эмпирической кривой обеспеченности рассмотрим на следу- ющем примере. Исходные данные – измеренные характеристики снеж- ного покрова в 1024 точках (табл. 7).

Таблица 7

Характеристики снежнoго пoкрова в точках измерений

Из табл. 7 выбраны максимальное и минимальное значения сум- марных запасов воды в снеге. Они равны соответственно 441 и 4 мм. Амплитуда изменения запасов воды разбита на интервалы по 20 мм. Далее подсчитано число точек измерения в пределах каждого интер-

вала и нарастающая сумма числа точек по мере уменьшения запасов воды в снеге по интервалам.

В табл. 8 приведен расчет распределения и нарастания числа точек с максимальными снегозапасами в пределах интервалов. При пересчете в проценты за 100% принималось общее число точек измерений, т. е. 1024. На рис. 49 приведены график распределения и кривая обеспеченности запасов воды в снеге, построенные по данным табл. 8. При построении

кривой обеспеченности значения обеспеченностей относились к нижним границам интервалов. По кривой обеспеченности можно определить зна- чения снегозапасов заданных обеспеченностей. Например, запас воды в снеге 102 мм имеет обеспеченность 20%, 44 мм – 80%.

Таблица 8

Распределение по площади водосбора суммарных запасов воды в снежном покрове (включая ледяную корку)

Однако изложенный прием построения эмпирической кривой обес-

печенности дает удовлетворительные результаты только при большом

248

числе членов ряда. Часто в гидрологических исследованиях эмпири- ческие кривые обеспеченности строятся и для коротких рядов. В этих случаях для расчета эмпирической кривой обеспеченности применяет- ся следующий прием.

Переменные исходного ряда располагаются в убывающем порядке.

Для каждого значения переменной ранжированного таким образом ряда вычисляется эмпирическая обеспеченность (в процентах) по формуле

где m – порядковый номер рассматриваемого члена в ранжированном ряду; n – общее число членов ряда.

Формула (57) используется в случаях, когда представлены все воз- можные значения переменной, что не всегда бывает. Поэтому в прак-

тических расчетах для определения обеспеченности используются иные формулы. Так, согласно СНиП 2.01.14–83, эмпирическая вероятность превышения Pm гидрологических характеристик (величин) определя-

ется по формуле

Smin

Рис. 49. График распределения (1) и кривая обеспеченности (2)

максимальных запасов воды в снеге

249