
- •ВВЕДЕНИЕ
- •7. Вопросы для контроля
- •Результаты эксперимента
- •1. Определите тип коагуляции.
- •3. Оцените влияние концентрации электролита на порог коагуляции, коагулирующую способность.
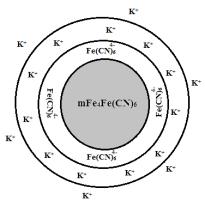
- •4. Что изображено на рис. 2.1?
- •2. Определить средний размер частиц и установить влияние концентрации золя на размер частиц.
- •Лабораторная работа № 6
- •Лабораторная работа № 7
- •ИССЛЕДОВАНИЕ СВОЙСТВ РАСТВОРОВ ПОЛИЭЛЕКТРОЛИТОВ
- •СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
- •ОГЛАВЛЕНИЕ

Концентрацию электролита в пробирке рассчитать в соответствии с молярностью раствора и заданным объемом электролита по формуле
Cэ = Сэ0 (Vэ (Vэ +Vв) , |
(2.1) |
где Cэ — концентрация рабочего раствора электролита, моль/л; Cэ0 — концентрация исходного раствора электролита, моль/л;
VЭ — объем раствора электролита в пробирке, мл; Vв — объем воды в пробирке, мл.
Расчет порога коагуляции провести по формуле
γ =CэVэ (Vэ +Vзоля ) , |
(2.2) |
где γ — порог коагуляции, моль/л; Cэ — молярность раствора электролита, моль/л; VЭ — минимальный объем электролита, достаточный для коагуляции золя, мл; Vзоля — объем золя, мл.
Результаты расчетов занести в табл. 2.1.
5. Обработка экспериментальных данных
В отчете описать вид образовавшегося коллоидного раствора, привести уравнение химической реакции и формулу мицеллы.
Заполнить табл. 2.1 «Условия и результаты эксперимента».
|
|
Условия и результаты эксперимента |
|
Таблица 2.1 |
|||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
№ |
Условия эксперимента |
Результаты эксперимента |
|||||||||
|
Объем, мл |
|
|
KCl |
|
|
AlCl3 |
||||
п/п |
|
|
|
|
|
||||||
|
вода |
электролит |
золь |
Cэ |
+/– |
γ |
|
Cэ |
|
+/– |
γ |
1 |
4 |
1 |
5 |
|
|
|
|
|
|
|
|
2 |
3 |
2 |
5 |
|
|
|
|
|
|
|
|
3 |
2 |
3 |
5 |
|
|
|
|
|
|
|
|
4 |
1 |
4 |
5 |
|
|
|
|
|
|
|
|
5 |
0 |
5 |
5 |
|
|
|
|
|
|
|
|
16
6. Выводы по работе
1.Определите тип коагуляции.
2.Оцените влияние заряда иона-коагулятора на порог коагуляции, коагулирующую способность иона.
3.Оцените влияние концентрации электролита на порог коагуляции, коагулирующую способность.
4.Что изображено на рис. 2.1?
Рис. 2.1. Задание по работе № 2
Дополните рисунок: что происходит с мицеллой под действием электролитов? Нарисуйте, как изменяется коллоидная частица.
7. Вопросы для контроля
1.Причины возникновения двойного электрического слоя.
2.Как меняется величина потенциала в ДЭС?
3.Электрокинетический ζ-потенциал.
4.Влияние индифферентных и неиндифферентных электролитов на ДЭС и ζ-потенциал.
5.Перезарядка коллоидных частиц неиндифферентными электролитами.
6.Перезарядка коллоидных частиц индифферентными электролитами.
17
7.Агрегативная устойчивость дисперсных систем. Коагуляция. Коалесценция.
8.Факторы стабилизации дисперсных систем.
9.Порог коагуляции. Коагулирующая способность.
10.«Медленная» и «быстрая» коагуляция.
11.Правила Шульце — Гарди.
12.Лиотропные ряды.
13.«Неправильные» ряды.
14.Основы теории ДЛФО.
15. Нейтрализационная и концентрационная коагуляция.
Лабораторная работа № 3 ОПТИЧЕСКИЕ СВОЙСТВА ЗОЛЕЙ
1. Краткое теоретическое введение
Явление рассеяния света коллоидными системами наблюдал еще Фарадей (1857), исследовавший золи золота. Тиндаль установил, что светорассеяние удобно наблюдать на темном фоне при пропускании пучка света через золь сбоку. Особенно четко оно заметно при фокусировании света внутри коллоидной системы, когда образуется светящийся конус (конус Тиндаля). Само это явление часто называют эффектом Тиндаля. В дальнейшем было установлено, что светорассеяние не является особенностью гетеро- генно-дисперсных систем. В совершенно однородной среде свет не должен рассеиваться. В соответствии с принципом Гюйгенса каждую точку среды, до которой дошел волновой фронт, можно рассматривать как новый источник колебаний. Эти вторичные колебания усиливают друг друга в направлении распространения волны и гасятся в других направлениях. Рассматривая распространение волнового фронта, можно заключить, что в однородной изотропной среде он всегда остается геометрически подобным себе: например, плоская волна будет оставаться плоской. Если же на пути распространения плоской волны появляется местная
18
неоднородность (с другим показателем преломления), то каждая точка неоднородности станет самостоятельным центром колебаний. Возникает фронт волны, направление которого меняется и зависит от размера неоднородности. Если размер неоднородности значительно больше длины волны, то в основном наблюдается отражение по соответствующим законам. Если длина волны больше размера неоднородности, колебание рассеивается по всем направлениям. В этом случае колебания, исходящие от каждой точки неоднородности, не имеют определенных разностей фаз и более или менее усиливают друг друга во всех направлениях. Так возникает рассеяние света во все стороны. Рассеяние возможно только тогда, когда неоднородности находятся на расстояниях, друг от друга больших, чем длина волны. Сами же неоднородности должны иметь размеры меньше длины волны. Голубоватое свечение дисперсных систем, являющееся следствием светорассеяния, называ-
ется опалесценцией.
Теория светорассеяния для сферических, не поглощающих свет частиц, была развита Рэлеем.
Согласно теории, развитой Рэлеем, предполагается, что сферические частицы в дисперсной системе находятся настолько далеко
друг от друга, что можно |
пренебречь |
вторичным рассеянием, |
и поэтому интенсивность |
рассеянного |
света пропорциональна |
числу частиц в единице объема, или численной концентрации дисперсной системы v. Формула Рэлея для интенсивности света Iр, рассеянного единицей объема дисперсной системы со сферическими частицами, которые значительно меньше длины волны падающего света (не более 0,1λ), на расстоянии R от частиц в направлении, составляющем угол θ с направлением распространения излучения, имеет вид:
|
|
|
νυ2 |
|
(1+cos2 |
|
, |
(3.1) |
||
I p |
= I |
0 F |
|
|
|
|
θ) |
|||
λ |
4 |
R |
2 |
|||||||
|
|
|
|
|
|
|
|
|
||
где I0 — интенсивность падающего света; υ — объем частицы.
19
Функция от показателей преломления F определяется соотношением
|
n2 |
−n2 |
|
2 |
|
F = |
1 |
0 |
|
. |
(3.2) |
2 |
|
2 |
|||
n1 |
+ 2n0 |
|
|
||
Отсюда следует, что рассеяние может отсутствовать и в неоднородной среде, если показатели преломления дисперсной фазы (n1) и дисперсионной среды (n2) одинаковы.
Закономерность, выведенная Рэлеем, перестает выполняться, если размеры частиц дисперсной фазы приближаются к длине волны падающего света. Закон Рэлея не выполняется для дисперсных систем с частицами, поглощающими свет. Селективно поглощают свет, например, металлические частицы, что обусловливает, кроме того, сложную зависимость цвета прошедшего света от размеров частиц.
Частицы должны быть неэлектропроводны и должны иметь сферическую форму.
К основным методам исследования, использующим явление рассеяния света, принадлежат турбидиметрия, ультрамикроскопия и нефелометрия.
Турбидиметрия
Турбидиметрический метод исследования основан на измерении интенсивности света, прошедшего через дисперсную систему. Интенсивность падающего светового потока ослабляется в результате его рассеяния дисперсной системой. Если принять рассеянный свет за фиктивно поглощенный, это позволит получить простое соотношение, аналогичное закону Бугера — Ламберта — Бера для поглощения света молекулярными растворами. Ослабление интенсивности света dI пропорционально интенсивности падающего света I и приращению толщины слоя исследуемой системы dx:
dI =τ / dx , |
(3.3) |
где τ — мутность: коэффициент пропорциональности, характеризующий способность системы рассеивать свет.
20
Оптическая плотность A связана с мутностью соотношением
A = ln(I0 / Iп ) =τ l , |
(3.4) |
где In — интенсивность прошедшего света через кювету толщиной l.
Преимущество турбидиметрического метода исследования состоит в простоте подготовки и проведения измерений. Для турбидиметрических измерений можно использовать широко распространенные фотоэлектроколориметры, предназначенные для определения оптической плотности цветных молекулярных растворов. Точность турбидиметрического метода небольшая, поскольку интенсивность рассеяния (относительно малая величина) определяется по разности двух больших значений интенсивностей падающего и проходящего света.
Согласно теории Рэлея, интенсивность рассеянного света в бесцветном золе пропорциональна числу частиц в единице объема
и размеру дисперсных частиц: |
|
I р = I0 [k λ−n ], |
(3.5) |
где k — константа, зависящая от показателей преломления дисперсионной среды и дисперсной фазы; λ — длина волны падающего светового пучка; n — величина, пропорциональная размеру частиц.
Для определения интенсивности рассеяния в работе с помощью фотоколориметра измеряется светопропускание T (%):
T = In / I0 100% . |
(3.6) |
Величина светорассеяния R (%), по определению, — отношение интенсивностей рассеянного (Ip) и падающего света:
R = Iр / I0 100% . |
(3.7) |
Однако величину светорассеяния можно рассчитать, зная T:
R =100 −T . |
(3.8) |
Из уравнений (3.5) и (3.8) получаем |
|
I р = R I0 100% = I0 [k λ−n ] , |
|
R 100 = k λ−n . |
(3.9) |
21
Прологарифмируем уравнение (3.9):
lg R 2 = lg[k l−n ],
2 lg R = lg k −n lg l,
lg R = −n / 2 lg l +lg k / 2. |
(3.10) |
Если концентрация частиц в растворе постоянна и известна длина волны, то величину n можно рассчитать из уравнения (3.10). Для этого необходимо определить R при прохождении светового пучка через коллоидную систему с использованием различных светофильтров при различных длинах волн.
Применение метода ограничивается золями, отличающимися сравнительно высокой мутностью.
Ультрамикроскопия
Оптический метод наблюдения и анализа коллоидных частиц в жидкой или газовой фазе с помощью ультрамикроскопов. Достаточно разбавленный коллоидный раствор пропускают через ячейку, сильно освещенную сбоку. Когда дисперсные частицы проносятся через освещенную зону, в микроскопе видны вспышки света. Подсчитав число таких вспышек в определенный промежуток времени, можно определить концентрацию частиц.
Нефелометрия
Нефелометрический метод исследования основан на измерении интенсивности света, рассеянного дисперсной системой. Более высокая чувствительность и точность этого метода по сравнению с достигаемой в турбидиметрии позволяют определить не только концентрацию и размер частиц в золях, но и форму частиц, межчастичные взаимодействия и другие свойства дисперсных систем. В основе нефелометрии лежит уравнение Рэлея. Для измерения используются специальные приборы — нефелометры.
Молекулярным рассеянием объясняется голубой цвет неба (рассеянный свет) и его красный цвет (проходящий свет), когда солнце находится низко над горизонтом, а его лучи проходят большой слой рассеивающей среды.
22
