МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего образования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

ИЯТШ ОЯТЦ

Отчет

по лабораторной работе №4

Решение алгебраических и трансцендентных уравнений численными методами

Работа с файлом

Выполнила студентка группы 0А23

Шевченко А. В.

Проверил преподаватель

Дериглазов А.А.

Томск-2022

Оглавление:

Цель работы 3

Задание 3

Теоретическая часть: 4

Ход работы 8

Цель работы

Ознакомиться с некоторыми численными методами решения алгебраических и трансцендентных уравнений. Научиться реализовывать данные методы программно на языке Си.

Задание

1. Получить номер варианта задания у преподавателя, ведущего лабораторные занятия.

2. Ознакомиться с заданием к лабораторной работе (файл Задания.doc).

3. Ознакомиться с учебно-методическими указаниями к лабораторной работе (файл Лаб_4.doc).

4. Составить блок-схему алгоритма программы.

5. Набрать текст программы на языке Си с помощью текстового редактора.

6. Провести трансляцию и компоновку программы.

7. Выполнить контрольный запуск разработанной программы на исполнение.

8. Составить отчет по лабораторной работе в соответствии с правилами оформления отчета (файл Общие_указания_к_лабораторным_работам.doc).

Вариант 19

Определить на заданном интервале изменения переменной x корни уравнения вида F(x) = 0, используя предложенный в варианте задания метод. Границы интервала, коэффициенты уравнения, точность решения и начальные приближения ввести с терминала. Предусмотреть возможность поиска решения при одном запуске программы при других начальных условиях (границы, коэффициенты) и задаваемой точности.

Результаты решения вывести на экран и в файл вместе с заданными начальными условиями и видом решаемого уравнения.

Теоретическая часть:

Во многих научных и инженерных задачах возникает необходимость решения уравнений вида:

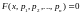, (1)

где F - заданная функция, x - неизвестная величина, p1, p2,..pn - параметры задачи.

Решениями или корнями уравнения (1) называются такие значения х, которые при подстановке в уравнение обращают его в тождество.

Только для простейших уравнений удается найти решение в аналитическом виде, т.е. записать формулу, выражающую искомую величину х в явном виде. В большинстве же случаев приходится решать уравнение вида (1) численными методами. Хотя иногда, даже при наличии аналитического решения, имеющего сложный вид, бывает проще провести численное решение по известному алгоритму, чем программировать громоздкую аналитическую формулу.

Численное решение уравнения (1) обычно проводят в два этапа.

На первом этапе необходимо определить интервал изменения переменной х, где расположен один корень или, что означает то же самое, определить достаточно хорошее приближение окрестности этой точки.

На втором этапе тем или иным численным методом определяется величина х, соответствующая корню уравнения (1) с заданной погрешностью.

Для решения второй задачи существуют многочисленные методы, из которых мы рассмотрим лишь три:

метод половинного деления;

метод Ньютона;

метод секущих.

Метод Ньютона

Предположим, что у нас определено начальное приближение х₀ к одному из корней уравнения (1). Тогда в точке х₀ можно вычислить левую часть решаемого уравнения .

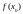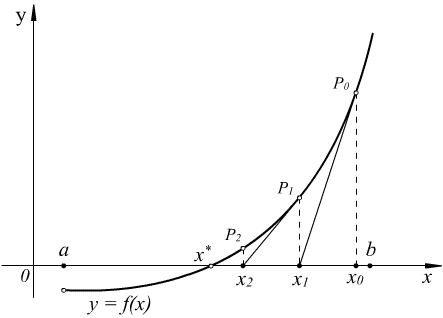
Рисунок 1 – Метод Ньютона

Рассмотрение метода Ньютона начнем с его геометрического представления (рисунок ). Возьмем точку х₀ отрезка [a, b] и проведем в точке P₀ с координатами касательную к кривой y =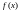 до пересечения с осью 0х. Получим значение х₁, в котором касательная пересекает ось 0x. Угловой коэффициент касательной равен значению производной от функции в точке касания. Следовательно, уравнение касательной, проходящей через точку с координатами имеет вид:

.

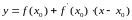Полагая y = 0, находим точку пересечения касательной с осью 0х, которую обозначим через х₁:

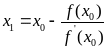
Абсциссу х₁ точки пересечения можно взять в качестве приближенного значения корня. Проведя касательную через новую точку с координатами и находя точку ее пересечения с осью 0х, получим второе приближения корня х₂ . Аналогично определяются последующие приближения.

Следующие приближения находим соответственно по формулам:

……………………

В общем случае для k-го шага итерационного процесса последнее соотношение принимает вид:

Из формулы Error: Reference source not foundError: Reference source not found вытекает необходимость вычисления значения производной функции в каждой точке. Процесс нахождения корня может считаться законченным, когда модуль отношения значения функции в точке x_k к ее производной меньше заданной величины погрешности 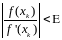, т.е. когда выполняется следующее условие:

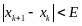
Таким образом, для реализации метода Ньютона необходимо:

Задать в явном виде уравнение , корни которого необходимо определить.

Определить первую производную функции в аналитическом виде.

Определить начальное приближение х₀, обеспечивающее быструю сходимость метода.

Задать точность нахождения корня уравнения .

Реализовать в программе итерационную процедуру, реализующую формулу Error: Reference source not found.

Модифицированный метод Ньютона

Алгоритм поиска корня уравнения (1) повторяется практически также как в искомом методе Ньютона с единственным исключением, производная вычисляется лишь на первой итерации и далее это значение используется на следующих итерациях. Рекуррентное соотношение для уточнения корня будет выглядеть так Error: Reference source not found:

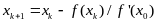
Ход работы

Численное решение уравнения проводят в два этапа, поэтому программа будет разделена на две части.

Первая часть.

1.1 Определяется промежуток изоляции корня, то есть находим интервал, на котором корень уравнения существует и единственный.

1.2 Объявляются переменные a, b которые являются границами интервалов, также n – число разбиений и h – шаг.

1.3 Шаг находится по формуле: h = (b - a) / n;

1.4 С помощью цикла for рассматриваем изменение функции f(x) с шагом x = x + h;

1.5 С помощью условия if (x < b && f(x) * f(x + h) < 0) выполняем проверку в каком промежутке изоляции находится корень и сколько их.

1.6 Вывод количества корней на экран.

Вторая часть. Проверка условия на сходимость от производных данной функции

2.1 f = a0 + (a1 * sin(a2*x)) + (a3 * log(x))

2.2 По основной формуле метода Ньютона находим корень уравнения, подставляем в функцию и поверяем данное условие:

2.3 Выводим корень на экран.

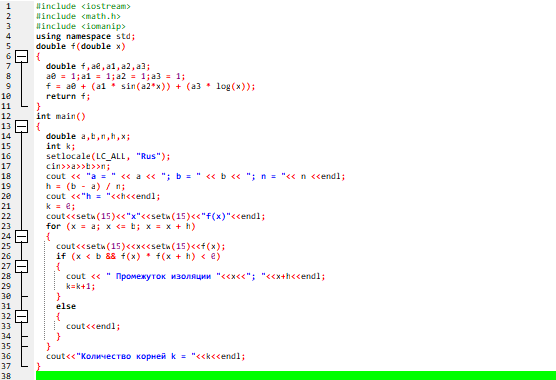
Рисунок 1 – Первая часть Кода

Рисунок 2 – Вывод значений 1

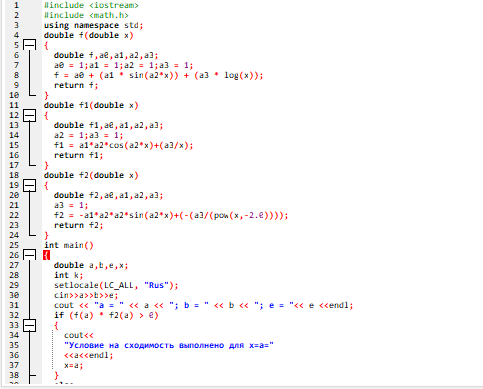
Рисунок 3 – Вторая часть кода

Рисунок 4 – Вторая часть кода

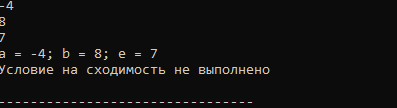
Рисунок 5 –Вывод значений 2

Вывод

Входе работы было произведено ознакомление с некоторыми численными методами решения алгебраических и трансцендентных уравнений. Получены навыки реализовывать данные методы программно на языке С++.