Ход работы
Ознакомились с методикой построения математической модели теплообменника.
Построили математическую модель ректора идеального смешения:
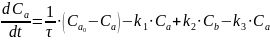
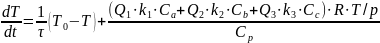
Построили математическую модель идеального вытеснения:
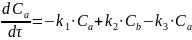
Разработали алгоритм и программу расчета каждой модели (Приложение А и В). Программы использованы для расчёта текущих значений концентраций на выходе из реакторов, а также для исследования влияния времени контакта на выход продуктов реакций.
Исследовали динамический режим работы реактора идеального смешения и идеального вытеснения. Результаты представлены в приложениях Б и Г, а также на рисунках 3 – 8.
Выполнили анализ результатов. Сделали выводы.
Результаты исследования
Рисунок 3 – Зависимость концентраций реагирующих веществ от времени в реакторе идеального смешения
Рисунок 4 – Зависимость температуры от времени в ректоре идеального смешения
Рисунок 5 – Зависимость степени превращения компонентов от времени в реакторе идеального смешения
Рисунок
6 – Изменение концентрации компонентов
в реакторе идеального вытеснения от
времени
Рисунок 7 – Зависимость изменения температуры в ректоре идеального вытеснения и теплоносителя от времени контакта
Рисунок 8 – Зависимость степени превращения компонентов от времени контакта в реакторе идеального вытеснения
Вывод
В результате лабораторной работы составили математическую модель ректора идеального смешения и идеального вытеснения, сформировали алгоритм расчета и программу вычислений. На основании полученных результатов можно судить об изменении концентрации веществ и температуры в реакторе, рассчитать степень превращения компонентов.
На основании рисунка 5 видно, что в реакторе идеального смешения при увеличении времени контакта с 1 до 6 секунд степень превращения возрастает с 55 % до 83 %. Для повышения степени превращения компонентов рекомендуется увеличить время контакта. Что касается целевого продукта (гексана), при времени контакта 3 секунды реактор достигает стационарного режима через 3 секунды, а при времени контакта 6 секунд – через 4 секунды (рисунок 3).
В реакторе идеального вытеснения достигаются более высокие значения степени превращения компонентов — до 99 % (рисунок 8). Таким образом, данный тип реактора является наиболее эффективным для проведения рассматриваемой реакции.
Приложение a
import math
import matplotlib.pyplot as plt
C0 = [0.0328, 0.0, 0.0]
k = [0.25, 0.1, 0.25]
Ea = [87230, 104750, 78610]
Q = [6280, -6280, 10640]
dt, tk, T0 = 0.01, 10.0, 660
arr_tau = [1,2,3,4,5,6]
arr_tau_hl = [1,2,3,4,5,6]
Vap = 10 #m3 объем аппарата
F = Vap*(1/3)*2*5 # m2 - площадь теплообмена
K = 15 # Вт/(м2*К)
Vhl = 100 # m3
Tg0 = 720 # K теплоноситель
# коэффициенты температурной зависимости для расчета теплоемкости
a =[[-1.054, 1.390e-1, -7.449e-5],
[-2.524, 1.477e-1, -8.533e-5],
[-3.489, 1.469e-1, -8.063e-5]]
n = 3
m = 3
R=8.314
R1=0.00845
PP=0.103
PP_g=0.203
Cp_g = 200 # Дж/(моль*K)
def pr(c, k, Q, tem, tem_g, ind_tau):
s = sum(c)
cc = [c[i]/s for i in range(n)]
Cp = 0
f = [0 for i in range(n+2)]
for i in range(n):
Cp+= (a[i][0]+a[i][1]*tem+a[i][2]*tem*tem)*4.1887*cc[i]
f[0]=1/arr_tau[ind_tau]*(C0[0]-c[0])-k[0]*c[0]+k[1]*c[1]-k[2]*c[0]
f[1]=1/arr_tau[ind_tau]*(C0[1]-c[1])+k[0]*c[0]-k[1]*c[1]
f[2]=1/arr_tau[ind_tau]*(C0[2]-c[2])+k[2]*c[0]
f[3]=1/arr_tau[ind_tau]*(T0-tem)+(-Q[0]*k[0]*c[0]-Q[1]*k[1]*c[1]-Q[2]*k[2]*c[2] + K*F/Vap*(tem_g-tem))*R1*tem/PP/Cp
f[4]=1/arr_tau_hl[ind_tau]*(Tg0-tem_g)+(-K*F/Vhl*(tem_g-tem))*R1*tem_g/PP_g/Cp_g
return f
k0 = [k[i]/math.exp(-Ea[i]/(R*T0)) for i in range(m)]
nn=int(tk/dt/10)
print(' Результаты расчёта')
print('Таблица 1 – Расчёт РИC в нестационарном режиме политропический режим')
t = 0
c = C0[:]
tem = T0
tem_g = Tg0
jn = 0
for ind_tau in range(len(arr_tau)):
c_pl1 = []
c_pl2 = []
c_pl3 = []
tem_pl = []
tem_g_pl = []
print('Время, с A B C T,K Tгор,К Xa')
print('Время контакта='+str(arr_tau[ind_tau])+' c')
print(f'{t:.1f}', ' ', f'{c[0]:.4f}', ' ', f'{c[1]:.4f}', ' ', f'{c[2]:.4f}', ' ',f'{tem:.4f}', ' ',f'{tem_g:.4f}', ' ', f'{0:.4f}')
while t<=tk:
t+=dt
jn+=1
k=[k0[i]*math.exp(-Ea[i]/(R*tem)) for i in range(m)]
f = pr(c,k,Q,tem, tem_g, ind_tau)
c = [c[i]+dt*f[i] for i in range(n)]
c_pl1.append(c[0])
c_pl2.append(c[1])
c_pl3.append(c[2])
tem += dt*f[n]
tem_g += dt*f[n+1]
tem_pl.append(tem)
tem_g_pl.append(tem_g)
if jn==nn:
xa = (C0[0]-c[0])/C0[0]
print(f'{t:.1f}', ' ', f'{c[0]:.4f}', ' ', f'{c[1]:.4f}', ' ', f'{c[2]:.4f}', ' ',f'{tem:.4f}', ' ',f'{tem_g:.4f}', ' ', f'{xa:.4f}')
jn=0
t = 0
c = C0[:]
tem = T0
tem_g = Tg0
jn = 0
x = [i*dt for i in range(int(tk/dt)+1)]
plt.plot(x,c_pl1,x,c_pl2,x,c_pl3)
# In[11]:
x = [i*dt for i in range(int(tk/dt)+1)]
plt.plot(x,tem_pl, x,tem_g_pl)