7. Исследование показателей качества замкнутой системы, корректирования динамических свойств исходной системы и исследование скорректированной системы

Дано:

Максимальная производная входного сигнала равна единице:

Определим минимальный порядок астатизма системы:

Минимальный коэффициент усиления:

Выберем рад/с

Параметры желаемой системы:

Построим передаточную характеристику желаемой системы:

Выражение для корректирующего звена:

х_М.в.1

х_М.в.2

Рисунок 65 – Блок-схема системы после коррекции

Рассчитаем значения ошибок при детерминированных мешающих воздействиях, приложенных к выходу системы X_мв2(t) и к выходу дискриминатора X_мв1(t):

В частотной области:

Пересчитаем на входную систему:

В частотной области:

Суммарная ошибка:

Средняя квадратическая ошибка системы под воздействием помех:

Преобразуем подынтегральное выражение к виду:

Тогда:

Так как максимальная степень полинома знаменателя , то для вычисления интеграла :

Коэффициенты знаменателя	Коэффициенты числителя
a0 =	b0 = 0
a1 =	b1 = 0
a2 =	b2 =
a3 =	b3 = 1
a4 =

Исследование переходной характеристики системы при ступенчатом задающем воздействии:

Рисунок 66 – Модель скорректированной замкнутой системы

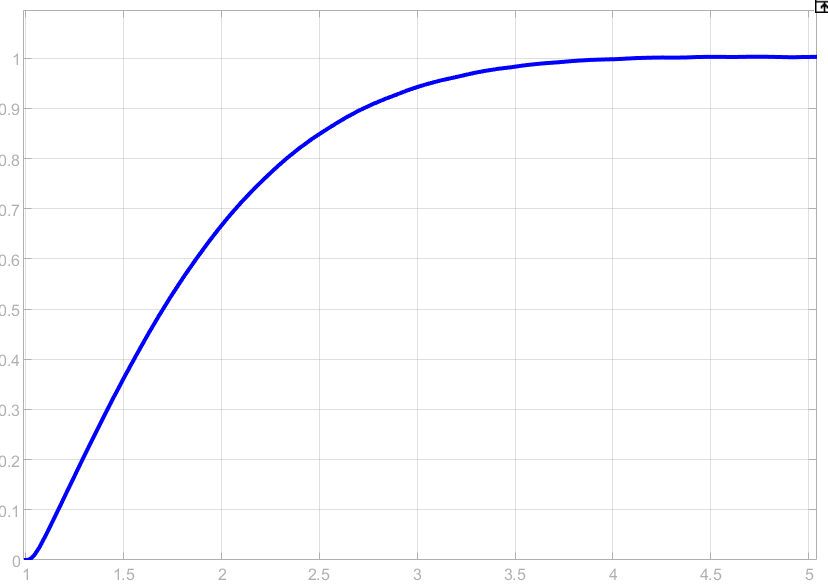
Рисунок 67 – Переходный процесс при ступенчатом входном воздействии

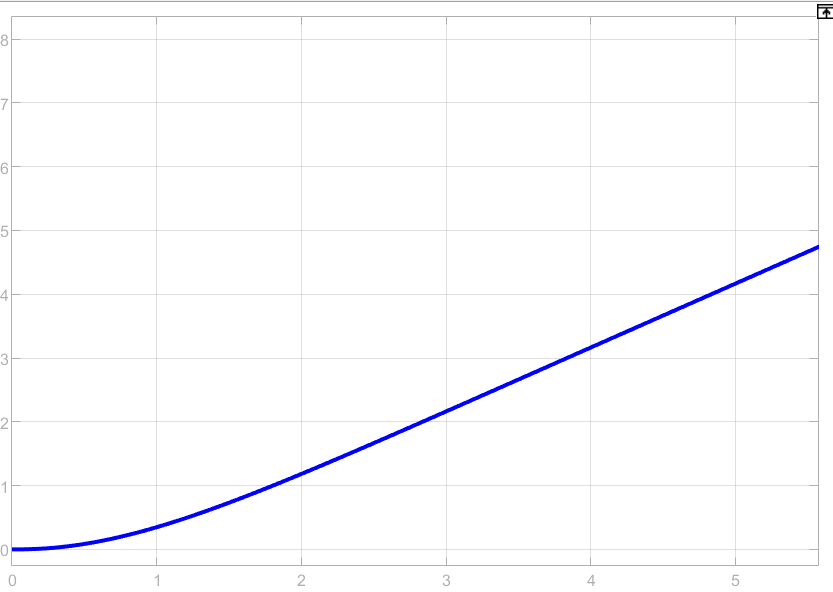
Рисунок 68 – Переходная характеристика при линейном входном воздействии

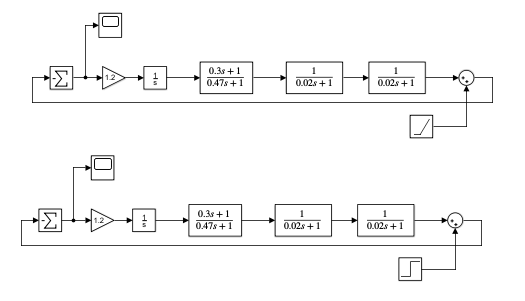
Рисунок 69 – Модель скорректированной системы с мешающим воздействием

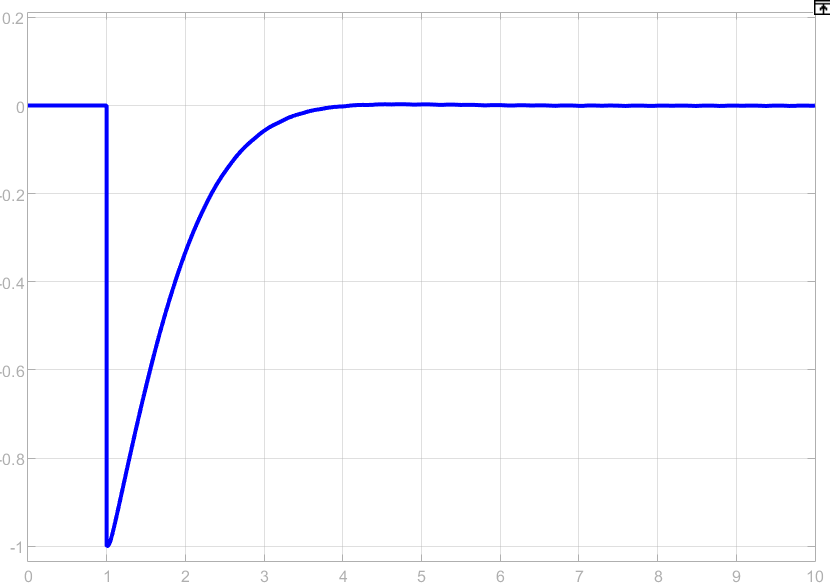
Рисунок 70 – Переходная характеристика сигналов ошибок при ступенчатом мешающем воздействии

Рисунок 80 – Переходная характеристика сигналов ошибок при линейном входном воздействии

9. Расчет скорректированной системы по варианту после включения в нее нелинейного звена. Систему при этом рассматриваем как непрерывную и нелинейную.

а) рассчитаем и построим эквивалентные нормированные коэффициенты передачи и для нелинейного звена НЗ₁ с S-образной треугольной характеристикой и нелинейного звена НЗ₂ – звена с линейной зоной и насыщением.

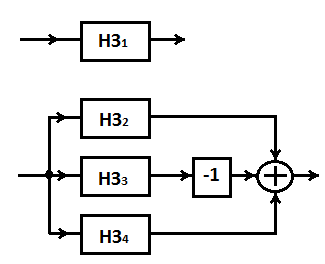
Рисунок 81 – Схема скорректированной системы с включением нелинейных звеньев

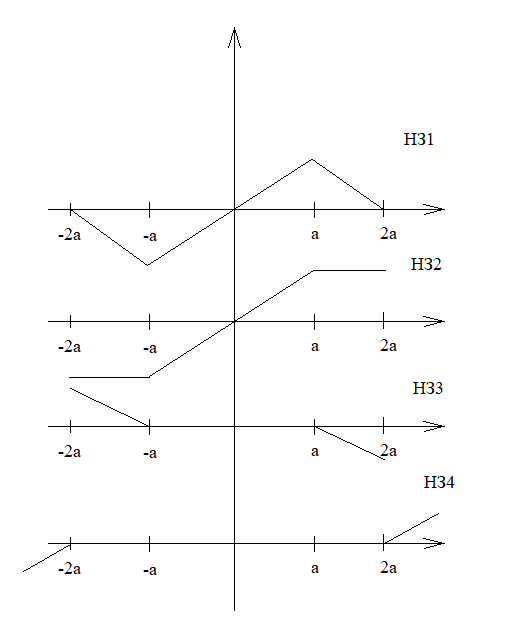
Рисунок 82 – S-образные статические характеристики нелинейных звеньев

Представим нормированный коэффициент передачи нелинейного звена НЗ₁ в виде суммы:

Тогда для первого нелинейного звена:

Для второго нелинейного звена:

Для анализа возможности возникновения автоколебаний данную выше величину необходимо перевести в логарифмический масштаб.

Составим таблицу рассчитанных значений для каждого из представленных в задании звеньев.

Таблица 9. Рассчитанные значения коэффициентов для каждого из нелинейных звеньев

	1	2	3	4	5	6	7	8	9	10
	1,69	0,22	0,05	0,02	0,01	6,02	3,77	2,52	1,76	1,28
	0,59	4,59	19,25	47,79	95,14	166	265,2	397,36	567,2	779,46
	-4,58	13,23	25,69	33,59	39,57	44,4	48,37	51,98	55,08	57,84
	1	0,61	0,42	0,32	0,25	0,21	0,18	0,16	0,14	0,13
	1	1,64	2,4	3,18	3,95	4,73	5,52	6,3	7,08	7,87
	0	4,31	7,61	10,04	11,94	13,51	14,83	15,99	17,01	17,97

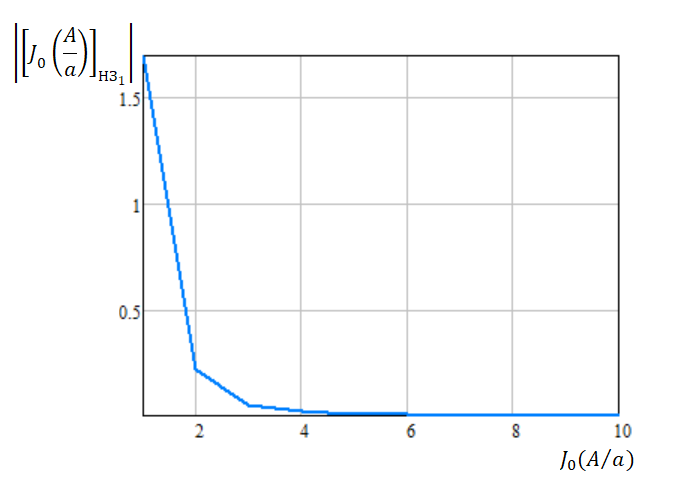
Рисунок 83 – График модуля эквивалентного нормированного коэффициента передачи звена

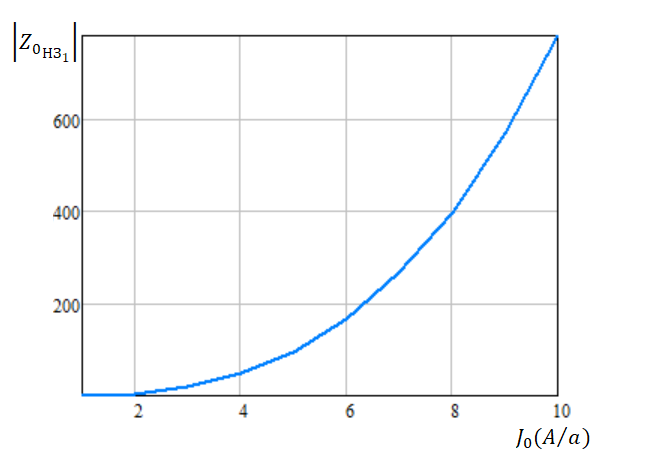
Рисунок 84 – График модуля звена

Рисунок 85– График звена

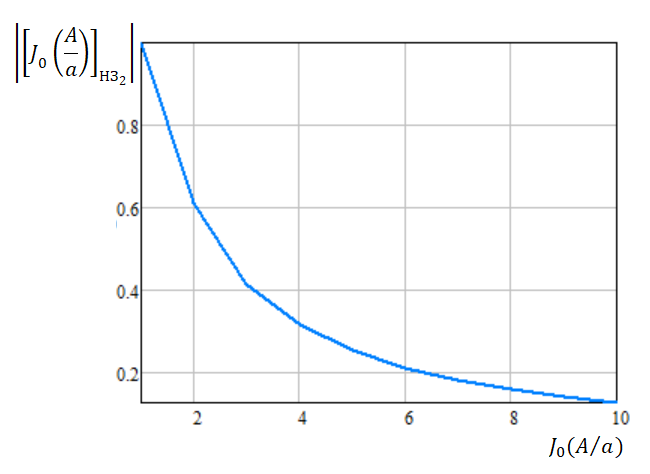
Рисунок 86 – График модуля эквивалентного нормированного коэффициента передачи звена

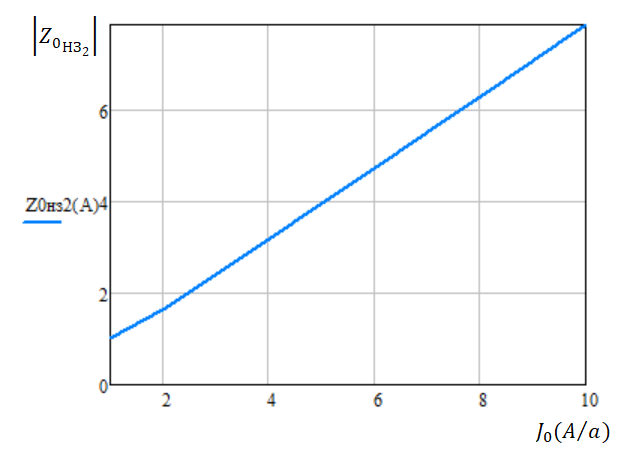
Рисунок 87 – График модуля звена

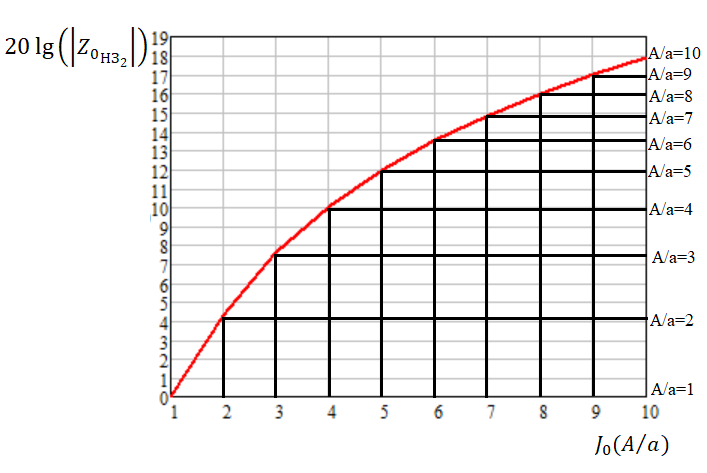
Рисунок 88 – График звена

б) проверяем методом гармонического баланса, используя логарифмическую плоскость, возможно ли возникновение автоколебаний в нелинейной системе по варианту, а если при параметрах желаемой системы автоколебания невозможны, то указываем минимально возможный коэффициент усиления скорректированной системы или К_на, при котором они возможны.

Согласно методу гармонического баланса, автоколебания в замкнутой системе возможны в том случае, если выполняются условия баланса фаз и баланса амплитуд (усиления):

Передаточная функция желаемой характеристики имеет вид:

Проверим выполнение условий баланса фаз и баланса амплитуд для системы с характеристикой:

При соблюдении баланса по фазе, у нас не соблюдается баланс по амплитуде. Из этого следует, что автоколебаний в системе не будет. Найдем такой коэффициент усиления , при котором будут выполняться оба условия.

Условия баланса фаз и амплитуд выполняются. Определим амплитуду автоколебаний. Зная из задания, что от , а зона линейности равна , амплитуда автоколебания:

Рассчитаем для системы с S-образной треугольной характеристикой предельные значения задающего воздействия:

В

В

В