Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра телевидения и управления (ТУ)

СИНТЕЗ ЦИФРОВЫХ ФИЛЬТРОВ ДЛЯ ОБРАБОТКИ ОДНОМЕРНЫХ СИГНАЛОВ

Отчет по лабораторной работе №2

по дисциплине «Цифровая обработка сигналов» Вариант №6

Выполнили Студенты гр. 730-1

Астра Г. А.

Подойницын К. В.

. .2023

Принял

Доцент кафедры ТУ

Каменский А. В.

. .2023

Томск 2023

Введение

Целью данной лабораторной работы является приобретение студентами навыков проектирования цифровых фильтров и оптимизации их параметров.

По варианту необходимо было взять фильтр Бесселя 4 порядка и следующие параметры: Q = 6, F_d = 1,75 * 10⁶, F₀ = 0,35 * 10⁶.

1 ХОД РАБОТЫ

1. Синтез режекторного фильтра

Были заданы значения частоты дискретизации входного сигнала, частоты собственных колебаний в контуре без потерь, добротность режекторного контура (рисунок 1.1).

Рисунок 1.1 – Заданные параметры

По имеющимся данным были получены графики АЧХ и ФЧХ фильтров, синтезированных различными методами: инвариантным преобразованием ИХ (AI(ω) и φI(ω)), отображением дифференциалов (AO(ω) и φO(ω)), Z-форм (AZ(ω) и φZ(ω)), билинейного преобразования (AB(ω) и φB(ω)) (рисунки 1.2-1.3).

Рисунок 1.2 – АЧХ режекторного ЦФ

Рисунок 1.3 – ФЧХ режекторного ЦФ

Метод билинейного преобразования является одним из основных часто используемых на практике методов синтеза цифровых фильтров. При этом преобразовании происходит трансформация частот.

При методе инвариантного преобразования. Необходимо правильно выбрать интервал дискретизации Т. Он определяет степень приближения частотных и временных свойств ЦФ к аналоговому фильтру. Чем меньше интервал дискретизации T, тем лучше степень приближения к ИХ аналогового фильтра-прототипа, но при этом увеличивается порядок фильтра.

В основе метода отображения дифференциалов лежит дискретизация аналогового фильтра-прототипа, заключающаяся в замене дифференциалов в его дифференциальном уравнении прямыми, обратными или центрированными разностями.

Метод Z-форм представляет собой дальнейшее развитие метода билинейного преобразования. Как и в методе билинейного преобразования, используется разложение ln(z) в ряд и учитывается большее число членов ряд.

2. Коррекция частоты

Для метода билинейного преобразования при синтезе режекторного фильтра производилась коррекция частоты. На рисунке 1.4 показаны АЧХ фильтра, где функции A(ω) соответствует график с дискретизацией без переопределения частоты настройки, а функции A1(ω) – график с переопределением частоты настройки.

Рисунок 1.4 – АЧХ ЦФ с переопределением частоты настройки и без него

На рисунке 1.5 показан ФЧХ фильтра, где φ(ω) – график с

дискретизацией без переопределения частоты настройки, φ1(ω) – график с переопределением частоты настройки.

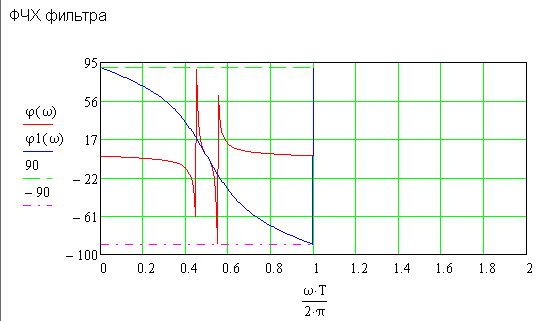
Рисунок 1.5 – ФЧХ ЦФ с переопределением частоты настройки и без него

При билинейном преобразовании (БЛП) происходит трансформация частот, потому что точно реализовать частотные свойства аналогового фильтра-прототипа нельзя.

3. Синтез заданного ЦФ НЧ 3-го порядка методом билинейного преобразования

Был задан порядок N = 4 аналогового фильтра-прототипа и затем была получена его ЧХ. При дискретизации ЦФ методом билинейного преобразования было проведено сравнение АЧХ и ФЧХ синтезированного ЦФ и аналогового фильтра-прототипа.

Полученный график АЧХ представлен на рисунке 1.6.

Рисунок 1.6 – АЧХ дискретного и аналогового фильтров

Графики ФЧХ и групповой задержки показаны на рисунке 1.7, где: функция φ(ω) – ФЧХ дискретного фильтра, функция φa(ω) – ФЧХ аналогового фильтра, τ(ω) – групповая задержка дискретного фильтра, функция τа(ω) – групповая задержка аналогового фильтра.

Рисунок 1.7 – ФЧХ дискретного и аналогового фильтров

Далее были вычислены коэффициенты, сами вычисления представлены на рисунках 1.8-1.11.

Рисунок 1.8 – Расчет коэффициентов (часть 1)

Рисунок 1.9 – Расчет коэффициентов (часть 2)

Рисунок 1.10 – Расчет коэффициентов (часть 3)

Рисунок 1.11 – Расчет коэффициентов (часть 4)

При синтезе фильтра Бесселя 4-го порядка были получены следующие значения коэффициентов:

Рисунок 1.12 – Значения коэффициентов

4. Частотные преобразования для ЦФ Бесселя

Используя коэффициенты, рассчитанные в предыдущем пункте, в программных модулях l_f_filt.mcd, u_f_filt.mcd, b_f_filt.mcd и r_f_filt.mcd были выполнены частотные преобразования для заданного фильтра. Полученные графики представлены на рисунках 1.13 – 1.16.

Рисунок 1.13 – Преобразование ФНЧ – ФНЧ1

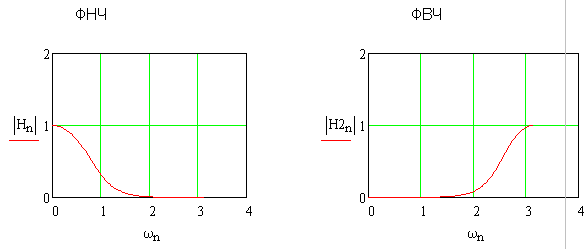
Рисунок 1.14 – Преобразование ФНЧ – ФВЧ

Рисунок 1.15 – Преобразование ФНЧ – ПФ

Рисунок 1.16 – Преобразование ФНЧ – РФ

5. Анализ влияния ошибок

Далее проводился анализ влияния ошибок задания коэффициентов цифрового ФНЧ на АЧХ с помощью изменения коэффициента b.

На рисунке 1.17 представлено сравнение АЧХ идеального фильтра и АЧХ фильтров при изменении коэффициентов b_1-3.

Рисунок 1.17 – АЧХ идеального фильтра и фильтров с измененными коэффициентами

На рисунке 1.18 наглядно представлена зависимость изменения функции ошибок от изменения коэффициента b_1-3.

Рисунок 1.18 – Функции ошибок

6. Квантование коэффициентов

Было проведено квантование коэффициентов цифрового фильтра с числом двоичных разрядов от 3 до 5 (рисунки 1.19-1.21).

Рисунок 1.19 – Отклонение АЧХ при числе разрядов n = 3

Рисунок 1.20 – Отклонение АЧХ при числе разрядов n = 4

Рисунок 1.21 – Отклонение АЧХ при числе разрядов n = 5

Таким образом увеличение разрядности при квантовании коэффициентов фильтра приводит к тому, что АЧХ фильтра все больше стремится к исходной. Также можно заметить, что при числе двоичных разрядов больше 3 максимальное отклонение АЧХ не превышает 10-20%.

Заключение

В ходе выполнения лабораторной работы были изучены основы анализа характеристик цифровых фильтров. В соответствии вариантом №6 были выполнены следующие задачи:

• синтез режекторного фильтра различными методами;

• для метода билинейного преобразования произведена коррекция частоты;

• произведен синтез фильтра Бесселя 4-го порядка методом билинейного преобразования;

• рассчитаны коэффициенты и изображена структурная схема фильтра Бесселя 4-го порядка;

• получены частотные преобразования цифрового фильтра;

• проанализировано влияние ошибок задания коэффициентов фильтра Бесселя 4-го порядка;

• проквантованы коэффициенты цифрового фильтра на такое число двоичных разрядов, чтобы максимальное отклонение АЧХ от заданной составляло порядка 10-20%.