Данная модель может быть задана с помощью матрицы вероятностей

где 1 - P0 – условная вероятность правильного приема (k+1)-го символа, если предыдущий принят верно; P0 – условная вероятность ошибки приема (k-1)-го символа, если предыдущий был принят верно; P1 – условная вероятность ошибки приема (k+1)-го символа при ошибочно принятом предыдущим символе; 1 - P1 – условная вероятность правильного приема (k+1)-го символа при ошибочном принятии предыдущего символа.

Средняя (безусловная) вероятность ошибки в этом канале находится из уравнения:

Отметим, что память канале связи вызывается различными причинами. Так, одной из них являются замирания в радиоканале. В проводных каналах причиной памяти принято считать коммутационное помехи, возникающие при переключении, что выводит канал связи из строя на некоторое время. Также причинами памяти могут быть особенности методов модуляции и демодуляции, например, при относительной фазовой модуляции происходят сдваивание ошибок.

Тема «Математическая модель линейных и нелинейных преобразователей случайных сигналов в каналах связи»

Изучаемые вопросы:

1.Математическая модель линейного преобразователя случайных сигналов в каналах связи.

2.Математическая модель нелинейного преобразователя случайных сигналов в каналах связи.

3.Математическая модель случайного преобразователя сигналов в каналах

связи.

Математическая модель линейного преобразователя случайных сигналов в каналах связи

При передаче информации по каналам связи принимаемые сигналы отличаются от переданных вследствие воздействия помех. Кроме того, различие сигналов обуславливается наличием в каналах связи линейных и нелинейных устройств. В связи с этим при анализе и синтезе элементов каналов передачи информации приходится решать задачи по определению параметров случайных сигналов и помех на выходе канала связи.

Вбольшинстве случаев решение подобных задач сводится к нахождению корреляционной функции (используются при временном анализе) или к нахождению спектральной плотности мощности, то есть энергетического спектра (используются при частотном анализе). При этом параметры элементов, через которые проходят сигналы, считаются заданными.

Всистемах передачи информации наиболее часто встречаются след. линейные преобр. Помехи или аддитивные смеси сигнала и помехи.

1.Фильтрация

2.Интегрирование и дифференцирование

3.Умножение на известную функцию времени

4.Временная задержка

Вкачестве примера далее рассмотрим процесс прохождения через линейный элемент случайного гауссовского процесса с нулевым математическим ожиданием m = 0 и дисперсией σ ≠ 0.

Любой линейный элемент с постоянными параметрами характеризуется передаточной функцией K(jω), а также импульсной реакцией g(t), под которой понимают полученное на его выходе колебание, при подаче на вход единичного импульса (дельта-ф-и).

Комплексная передаточная функция равна

где K(ω) – амплитудная частотная характеристика; φ(ω) – фазочастотная характеристика.

Передаточная функция и импульсная реакция в этом случае связаны друг с другом преобразованиями Фурье:

Y(t) = g( ) X (t − )d

0

Здесь нижний предел равен нулю, так как для физически реализуемых элементов g(t) = 0 при t < 0.

Линейные преобразования гауссовского случайного процесса не изменяют вида закона его распределения, то есть процесс на выходе остается

гауссовским, а изменяется только его параметры (дисперсия, корреляционная функция, спектральная плотность мощности).

Сначала определим функцию корреляции выходного процесса:

=M {X (t1 − 1 ) X (t2 − 2 )}g( 1 )g( 2 )d 1d 2 =

0 0

=BX ( + − )g( 1 )g( 2 )d d 2

0 0

Из данной формулы видно, что функция корреляции на выходе линейного элемента не зависит от моментов времени t1 и t2 по отдельности, а определяется значением их разности τ = t2 – t1, поэтому если на вход линейного устройства подается стационарный процесс, то и на его выходе это свойство сохраняется.

Далее рассмотрим частотный анализ и установим взаимосвязь между энергетическими спектрами на входе и выходе линейного элемента.

Для этого воспользуемся теоремой Винера-Хинчина:

Тогда

где |K(jω)|2 – квадрат модуля передаточной функции.

Если процесс является гауссовским, у которого плотность распределения равна

Тогда энергетический спектр и дисперсия

GY ( ) = GX ( ) K ( j ) 2 = K ( j ) = K = GX ( )K 2

D{Y (t)} = D{X (t)} K ( j ) 2 = K ( j ) = K = D{X (t)}K 2 = 2K 2

Выражение для дисперсии следует из того, что

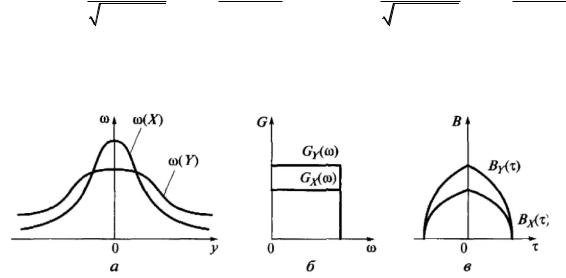
Линейные преобразования характеристик случайного процесса:

а – плотности распределения вероятностей; б – энергетического спектра; в – функции корреляции

Математическая модель нелинейного преобразователя случайных сигналов в каналах связи

Преобразование X → Y является однозначным, а обратное Y → X не всегда однозначное, как, например, квадратичная цепь с характеристикой Y = kX2.

При нелинейных преобразованиях спектр случайного процесса претерпевает значительные изменения. Изменяется также и вид закона распределение при прохождении случайных сигналов нелинейных элементов. Пусть на вход нелинейной системы подается смесь сигнала и шума:

X (t) = S (t) + n(t) ,

которая занимает сравнительно узкую полосу частот FC.

Вэтом случае на выходе системы будут присутствовать составляющие трёх видов:

1.Результаты биений (отклонений) частотных составляющих сигналов (С × С);

2.Результаты биений составляющих шумов (Ш × Ш);

3.Результаты биений сигнала и шума (С × Ш);

Вслучае, если известна характеристика нелинейной системы, а также

двухмерная плотность распределения ω(x1, x2; t1, t2) случайного процесса на