быть равномерно распределённой или иметь более сложный характер. Обычно её считают в таких каналах равномерно распределённой в интервале от 0 до
2π.
Данные каналы получили название каналов связи с общими райсовскими или рэлеевскими замираниями, поскольку соотношения между всеми составляющими спектра сигнала не изменяется при передаче. Условием применимости такой модели является узкополосность сигнала.
Такая модель достаточно хорошо описывает многие каналы радиосвязи в различных диапазонах волн.
Математическая модель многолучевого гауссовского канала связи с частотно-селективным замиранием
Такая модель соответствует ситуации, когда в точку приема приходит несколько лучей сигнала, имеющих различное время задержки τk k-го луча. Тогда сигнал может быть описан в виде:
n |
|
|
|
|
|
(t) − u(t − k )sin k |
|
z(t) = k (t) u(t − k )cos k |
|||
k =1 |
|
|
|
где n – число лучей в канале связи. |
|
|
|
В рассматриваемой модели канала связи условие |
t |
||
(t
) |
+ n |
|
|
1 / FС
(t) ,
обычно не
выполняются. Здесь FС – верхняя граничная частота спектра сигнала, а t – разность хода лучей (средняя разность времени распространения между лучами). Поэтому на разных участках спектра сигнала процессы замираний отличаются друг от друга, следовательно, могут наблюдаться значительные
искажения формы сигнала.
Данная модель, так же, как и предыдущая, широко применяется для отображения процессов передачи сигналов во многих реальных каналах радиосвязи.
Математическая модель каналов связи со сложной аддитивной помехой
Данный канал описывается любой и рассмотренных ранее моделей, но при этом к ним добавятся помехи других видов. То есть в этих каналах кроме шумовой гауссовской помехи с нулевым математическим ожиданием и спектральной плотностью G0(f) = N0 могут действовать сосредоточенные по спектру или времени помехи. Они тоже будут аддитивными, так как они складываются с передаваемым сигналом.
Сосредоточенные по спектру помехи могут образовываться сигналами посторонней радиостанции, излучением высокочастотных генераторов или создается преднамеренно в целях нарушения связи. В таком случае эти помехи будут узкополосными, модулированными квазигармоническими колебаниями. Их распределение такое же, как у полезных сигналов. Наибольшее влияние на качество каналов связи эти помехи будут оказывать в диапазоне коротких радиоволн.
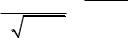
В случае импульсных помех, образованных короткими, одиночными импульсами, промежутки времени между такими импульсами значительно превышают время затухания сигнала от предыдущих посылок. Их причиной могут быть атмосферные и индустриальные помехи, создаваемые различной электрической аппаратурой, например, системой зажигания двигателя, от рентгеновских установок и др.
Вероятностное распределение этих помех описывается распределением амплитуд импульсов, которые подчиняется логарифмическому нормальному закону
|
|
|
(ln x−m) |
2 |
|
|
1 |
− |
|
||
(x) = |
2 |
2 |
|
||
|
e |
|
|
||
x |
2 |
|
|
|
|
|
2 |
|
|
|
|
,
где m и σ2 – математическое ожидание и дисперсия, соответственно, рассматриваемого случайного процесса.
Для описания вероятностных характеристик интервалов времени между импульсами применяется распределение Пуассона, согласно которому случайная величина λ принимает бесконечно счетное количество возможных значений с вероятностями
|
|
|
|
|
|
k |
|
|
|
P (k) = |
|
e |
− |
, k = 0, 1, ... |
|
|
|||
|
k! |
|
|
|
|
|
|
|
В наибольшей степени импульсные помехи оказывают воздействие на качество передачи информации в проводных каналах, а также в каналах радиосвязи в диапазоне сверхдлинных волн.
Математическая модель каналов связи с межсимвольной интерференцией
Данная модель соответствует случаю передачи информации с большой скоростью по каналу связи с ограниченной полосой пропускания. В связи с этим переходные процессы от предыдущих и последующих элементов сигнала способствуют появлению помех межсимвольной интерференции, приводящей к искажению текущего символа.
Данная модель также широко используется для описания процессов передачи информации в каналах проводной и радиосвязи. В радиоканалах причиной межсимвольной интерференции чаще всего является многолучевое распространение радиоволн. В каналах проводной связи межсимвольная интерференция вызывается нелинейностью фазочастотной характеристики канала с ограниченностью по полосе пропускания.
Например, пусть передается последовательность посылок ε длительностью T, которая соответствует цепочке из символов b-Q, b-Q-1, …, b-1, b0, …, bD-1, bD. Обозначим через Sr(t) отклик линейного
канала на посылку, соответствующую символу br. При этом выполняется условие
rT t (Q + r +1)T ,
где Q = T – относительная память канала, равная целой части дан-
ного отношения; t – время рассеивания (длительность переходного процесса в канале связи).
Тогда принимаемое колебание z(t) в интервале анализа
Ta
= (D +1)T
, где
D ≥ Q – задержка в числе символов принятия решения о передаваемом символе b0, будет иметь вид
z(t) = s |
(t) + |
0 |
|
g |
МСИ |
(t) + |
|
|
n(t)
,
где s0(t) – сигнал, соответствующий передаваемому символу b0; gМСИ(t) – сигнал межсимвольной интерференции, образованный посылками, переданными до и после анализируемого сигнала, n(t) – аддитивный гауссовский шум в канале связи.
Сигнал межсимвольной интерференции определяется по формуле
g |
МСИ |
(t) = |
|
|
g1(t) +
g |
2 |
(t) |
|
|
,
где g1(t) и g2(t) – посылки, переданные, соответственно, до и после анализируемого сигнала.
Сигнал, определяющий остаточный сигнал межсимвольной интерференции, образованный символами, переданными ранее символа b0 равен
1 |
−1 |
r |
|
|
|
||
g (t) = |
|
S |
(t − rT ) |
|
r =−Q |
|
|
Сигнал, определяющий сигнал межсимвольной интерференции, который образован символами, переданными после символа b0 равен
D
g2 (t) = Sr (t − rT ) r=1
Обычно, чем больше скорость передачи символов 1/T в канале связи с ограниченной полосой, тем большее число соседних посылок с сигналом s0(t)
будет определять сигнал gМСИ(t). В частном случае при Ta = T (т. е. при D = 0) сигнал g2(t) = 0.
Отметим, что при значительных уровнях шумов в канале с межсимвольной интерференцией предельное качество приема сигналов можно обеспечить только при оптимальных методах обработки. При этом, если передаваемый сигнал, помимо межсимвольной интерференции, подвергается другим искажениям, то рассмотренная модель существенно усложняется.