
- •Введение
- •Раздел «Методология построения современных систем связи»
- •Тема «Общие сведения о системах связи»
- •Основные термины и определения
- •Помехоустойчивые (корректирующие) коды
- •Тема «Основные характеристики сигналов и систем передачи информации»
- •Основные параметры сигналов
- •Основные характеристики систем передачи информации
- •Помехи и искажения в каналах связи
- •Виды дискретной модуляции сигналов
- •Раздел «Математические модели каналов связи»
- •Тема «Математические модели непрерывных каналов связи»
- •Классификация каналов связи
- •Математическая модель каналов связи с аддитивным гауссовским шумом
- •Математическая модель однолучевого канала связи с флуктуациями амплитуд и фаз сигналов (с гауссовскими общими замираниями)
- •Математическая модель многолучевого гауссовского канала связи с частотно-селективным замиранием
- •Математическая модель каналов связи со сложной аддитивной помехой
- •Математическая модель каналов связи с межсимвольной интерференцией
- •Тема «Математические модели дискретных каналов связи»
- •Основные характеристики дискретных каналов связи
- •Математическая модель дискретного симметричного канала связи без памяти
- •Математическая модель дискретного несимметричного канала связи без памяти
- •Математическая модель дискретного канала связи с памятью
- •Тема «Математическая модель линейных и нелинейных преобразователей случайных сигналов в каналах связи»
- •Математическая модель линейного преобразователя случайных сигналов в каналах связи
- •Математическая модель нелинейного преобразователя случайных сигналов в каналах связи
- •Математическая модель случайного преобразователя сигналов в каналах связи
- •Раздел «Помехоустойчивый прием дискретных и непрерывных сообщений»
- •Тема «Постановка задачи синтеза оптимального приемника»
- •Общий подход к задаче синтеза оптимального приемника
- •Критерий идеального наблюдателя
- •Оптимальный прием дискретных отсчетов сигналов
- •Оптимальный прием непрерывной реализации сигналов
- •Тема «Статистические критерии оптимального приема сигналов»
- •Критерий Неймана-Пирсона
- •Байесовский критерий минимума среднего риска
- •Тема «Синтез оптимального когерентного приемника в условиях аддитивного шума»
- •Синтез приемника дискретных отсчетов сигналов
- •Синтез приемника непрерывной реализации сигналов
- •Структурная схема оптимального когерентного приемника
- •Тема «Оптимальный когерентный приемник на базе согласованных фильтров»
- •Передаточная функция согласованного фильтра
- •Основные свойства согласованных фильтров
- •Структурная схема оптимального когерентного приемника
- •Трансверсальный согласованный фильтр с импульсной реакцией
- •Согласованный с прямоугольным радиоимпульсом фильтр
- •Тема «Анализ помехоустойчивости оптимального приема двоичных сигналов»
- •Помехоустойчивость сигналов с дискретной амплитудной модуляцией
- •Помехоустойчивость сигналов с дискретной частотной модуляцией
- •Помехоустойчивость сигналов с дискретной фазовой модуляцией
- •Сопоставительный анализ сигналов с дискретными видами модуляции
- •Повышение помехоустойчивости связи на основе методов разнесенного приема
- •Тема «Потенциальная помехоустойчивость оптимального приема непрерывных сообщений»
- •Общие сведения об обобщенном выигрыше
- •Обобщенный выигрыш при амплитудной модуляции
- •Обобщенный выигрыш при балансной и однополосной модуляции
- •Обобщенный выигрыш при фазовой модуляции
- •Обобщенный выигрыш при частотной модуляции
- •Раздел «Основы передачи и кодирования информации»
- •Тема «Основные характеристики источников дискретных и непрерывных сообщений»
- •Количество информации источника дискретных сообщений
- •Энтропия источника дискретных сообщений
- •Свойства энтропии источника дискретных сообщений
- •Избыточность источника дискретных сообщений
- •Производительность источника дискретных сообщений
- •Энтропия источника непрерывных сообщений
- •Тема «Пропускная способность дискретного канала связи»
- •Свойства условной энтропии дискретного канала связи
- •Свойства взаимной информации дискретного канала связи
- •Свойства пропускной способности дискретного канала связи
- •Пропускная способность двоичного симметричного канала связи без памяти
- •Тема «Пропускная способность непрерывного канала связи»
- •Пропускная способность непрерывного канала связи
- •Свойства взаимной информации непрерывного канала связи
- •Формула Шеннона для пропускной способности непрерывного канала связи
- •Влияние полосы пропускания непрерывного канала связи на его пропускную способность
- •Теоремы кодирования Шеннона для канала связи с помехами
- •Тема «Основы построения корректирующих кодов»
- •Классификация корректирующих кодов
- •Основные характеристики блочных корректирующих кодов
- •Обнаружение и исправление ошибок в коде
- •Линейные двоичные корректирующие коды
- •Пример задания линейного корректирующего кода
Производительность источника дискретных сообщений
Помимо избыточности, важным параметром, характеризующим любой источник с фиксированной скоростью выдачи сообщений, определяемая как 1/Tи, является его производительность
H '( A) = |
H ( A) |
= |
|
|
= |
1 |
= |
H ( A) |
|
|
|
и |
|
|
|||||
|
T |
|
|
|
T |
и |
|
||
|
|
|
|
|
|
|
|
||
|
и |
|
|
|
и |
|
|
||
При максимальной энтропии производительность равна
(14)
R |
= |
H |
max |
( A) |
= H |
|
( A) = log |
|
N = |
log |
2 |
N |
|
|
|
|
|
|
|||||||
|
|
|
max |
2 |
|
|
|
|||||
и |
|
|
T |
|
|
|
|
T |
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
и |
|
|
|
|
|
|
и |
|
|
Энтропия источника непрерывных сообщений
(15)
Рассмотрим источник непрерывных сообщений, на выходе которого в каждый момент времени t появляются сигналы S(t). Эти сигналы с бесконечно малой вероятностью могут принимать бесконечное число значений. Если бы сообщения могли передаваться по каналу абсолютно точно без искажений, то они содержали бы неограниченное количество информации. На самом деле изза помех и искажений количество информации, получаемой от такого источника, следует определять как разность энтропии до получения информации и после.
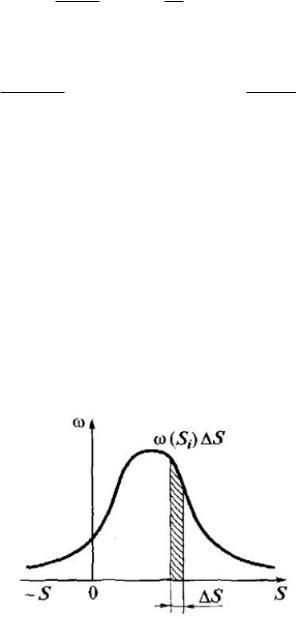
Обратимся к сигналу S(t), возможные значения которого в момент времени t характеризуются плотностью распределения вероятностей ω(S), показанной на рис. 2.
Рис 2. Плотность распределения вероятностей значений сигнала источника непрерывных сообщений.
Произведем квантование области значений S с шагом S. Вероятность попадания некоторого значения S в пределы i-ого шага квантования равна P(Si) ≈ ω(Si)ΔS. При этом приближение тем точнее, тем меньше интервал (шаг квантования S). Энтропия такого «дискретного» сигнала
|
|
|
|
|
|
|
|
1 |
(16) |
|
|
|
|
|
|
||||
M −log |
(S ) S |
|
= |
(S ) S log |
|
|
|||
|
2 |
i |
|
|
i |
2 |
(S ) S |
|
|
|
|
|
|
|
i |
|
|
i |
|
