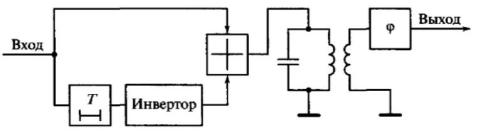
Схема такого фильтра:
T – линия задержки φ – фазовращатель
Фильтр состоит из колебательного контура высокой добротности, практически не имеющего потерь и настроенного на частоту ω0 = 2πf0, а также фазовращателя φ, сдвигающего фазу колебаний контура на φ0. Линия задержки на время T и инвертор обеспечивают гашение колебаний фильтра вне интервала t [0, T]. Импульсная реакция фильтра с учетом сдвига фаз
g(t) =U |
C |
cos( t − T − |
) =U |
C |
cos[ |
(T − t) + |
] =U |
C |
S(T − t) |
||
|
0 |
0 |
0 |
|
0 |
0 |
|
|
|||
Тема «Анализ помехоустойчивости оптимального приема двоичных сигналов»
Изучаемые вопросы:
1.Помехоустойчивость сигналов с дискретной амплитудной модуляцией.
2.Помехоустойчивость сигналов с дискретной частотной модуляцией.
3.Помехоустойчивость сигналов с дискретной фазовой модуляцией.
4.Сопоставительный анализ сигналов с дискретными видами модуляции.
5.Повышение помехоустойчивости связи на основе методов разнесенного приема.
Помехоустойчивость сигналов с дискретной амплитудной модуляцией
Определим вероятности ошибочного приема для двоичных сигналов с различными видами дискретной модуляции (манипуляции). Далее будут рассмотрены наиболее часто применяемые сигналы с амплитудной манипуляцией, частотной манипуляцией и относительной фазовой манипуляцией. Рассчитаем помехоустойчивость сигналов с дискретной амплитудной модуляцией. Принимаемые амплитудно-модулированные сигналы называют сигналами с пассивной паузой и описывают выражениями
S0 (t) = UC cos( 0t + ) , |
(1) |
S1 (t) = 0 , |
(2) |
где UC – амплитуда сигнала; ω – круговая частота сигнала; φ – начальная фаза (t [0, T]).
Квадрат расстояния между двумя сигналами (сигнальными точками) или эквивалентная энергия амплитудно-модулированных сигналов равна
|
|
|
|
|
|
T |
|
|
|
T |
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
2 |
d |
(S |
(t), S (t)) = E |
|
= |
|
S |
(t) − S (t) |
dt = |
|
S |
||
|
Э |
0 |
||||||||||
|
|
0 |
1 |
|
0 |
1 |
|
|
||||
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
(t)dt = E
(3)
Таким образом, векторное представление сигналов с амплитудной модуляцией будет иметь вид:
Векторное представление сигналов с АМ
Вероятность ошибочного приема амплитудно-модулированного сиг-
нала:
|
E |
|
|
|
|
|
|
|
|
|
h |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PАМ = 1 − F |
|
Э |
|
= 1 − F |
|
|
|
, |
(4) |
||||||
2N |
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
где F(x) – интеграл вероятности, h2 = E/N0 – отношение энергии сигнала |
|||||||||||||||
на входе приемника к спектральной плотности мощности белого шума. |
|
||||||||||||||
Интеграл вероятности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
t |
2 |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
||||
F ( x) = |
|
|
|
e |
2 |
dt |
|
|
|
|
(5) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для интеграла вероятности также существуют справочные таблицы. При расчетах важно учитывать следующие свойства интервала вероятности:
1.F(–∞) = 0
2.F(0) = 0.5
3.F(∞) = 1
4.F(–x) = 1 – F(x)
Помехоустойчивость сигналов с дискретной частотной модуляцией
В отличие от амплитудно-модулированных сигналов, частотно-модули- рованные сигналы называют сигналами с активной паузой и описывают выражениями:
S0 (t) = UC cos( 0t + 0 ) |
, |
|||
S (t) = U |
C |
cos( t + ) |
|
|
1 |
1 |
1 |
|
|
(6)
(7)
где t [0, T].
Кроме того, эти сигналы являются ортогональными: их скалярные произведения равны нулю:
(S |
, S ) = |
1 |
T |
S |
(t)S (t)dt = 0 |
(8) |
T |
|
|||||
|
|
|||||
0 |
1 |
|
|
0 |
1 |
|
|
|
|
0 |
|
|
|
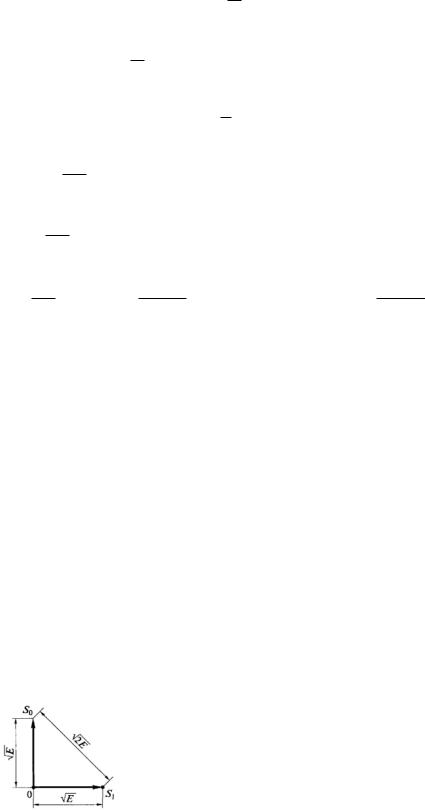
Пусть ω0 = 2πk0/T, ω1 = 2πk1/T, где k0 |
и k1 – целые числа, а φ0 и φ1 прини- |
||||||||||||||||||||||||||||||||||||||||
мают любые значения. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 = |
|
|
0 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
S |
|
|
(t)S (t)dt |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 = |
|
U |
|
cos( t + |
|
|
) U |
|
|
cos( t + ) dt |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
C |
0 |
C |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos x cos y = |
1 |
cos( x − y) + cos( x + y) |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
U |
2 |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 = |
C |
|
cos ( − )t + |
|
− |
+ cos ( + )t + |
|
+ dt |
(9) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2T |
|
|
|
|
|
0 |
|
1 |
|
|
|
0 |
|
|
|
|
|
1 |
|
|
|
|
0 |
|
1 |
|
|
|
0 |
|
|
1 |
|
|||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 = |
2 |
T |
cos ( |
− )t + |
|
− |
|
dt + |
T |
cos ( |
+ )t + |
|
+ dt |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
C |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2T |
|
|
|
|
0 |
|
1 |
|
|
0 |
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
1 |
|
|
|
|
0 |
1 |
|||||||||
|
U |
|
0 |
|
|
|
|
k |
|
− k |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
k |
|
+ k |
|
|
|
|
|
|
||||||||
0 = |
2 |
|
T |
|
|
|
|
|
|
t + 0 |
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
||||||||||||||||
|
C |
|
cos 2 |
|
0 |
|
1 |
− 1 |
dt + cos 2 |
|
0 |
|
1 |
t + 0 + 1 dt |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2T 0 |
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
T |
|
|
|
|
|
|
|
||||||
Правая часть равна нулю, так как подынтегральное выражение содержит целое число периодов косинусоид. Это доказывает ортогональность частотномодулированных сигналов.
Квадрат расстояния между сигнальными точками, или EЭ, описывается по формуле
|
|
T |
T |
T |
|
|
d 2 (S0 (t), S1 (t)) = EЭ = S0 (t) − S1 (t) 2 dt = S02 (t)dt − 2 S0 (t)S1 (t)dt + |
|
|||||
|
|
|
0 |
0 |
0 |
(10) |
T |
T |
|
|
T |
T |
|
|
|
|||||
+ S12 |
(t)dt = S0 |
(t)S1 |
(t)dt = 0 |
= S02 (t)dt + S12 (t)dt = E0 + E1 = 2E |
|
|
0 |
0 |
|
|
0 |
0 |
|
Данное выражение получено исходя из условий, что энергии каждой реализации равны друг другу. В двухмерном пространстве частотно-модулиро- ванные сигналы можно представить в виде векторов, расположенных друг относительно друга под углом π/2 (именно в этом случае их скалярное произведение будет 0).
Векторное представление сигналов с ЧМ.
Вероятность ошибки частотно-модулированных считать по формуле:
P |
= 1 − F |
|
E |
Э |
|
= 1 − F |
|
2E |
|
= 1 |
− |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
ЧМ |
|
2N0 |
|
2N0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
сигналов можно рас-
F ( |
h |
2 |
) |
(11) |
|
Помехоустойчивость сигналов с дискретной фазовой модуляцией
Так как и в случае с частотно-модулированными сигналами, фазомодулированные сигналы являются сигналами с активной паузой, поскольку каждая их реализации будет соответствовать двоичный информационный символ
«0» или «1».
В простейшем случае фазомодулированный сигнал образуются посредством скачкообразного изменения фазы несущего колебания на 180°. Получаемое в результате колебание будет представлять собой последовательность информационных двухполярных посылок, умноженных на гармоническое несущее колебание. Такие сигналы можно записать в виде
S0 (t) = UC cos( C t + ) ,
S1 (t) = UC cos( t + + ) = −UC cos( C t + ) ,
(12)
(13)
где t [0, T].
Из формул (12) и (13) следует, что S1(t) = –S0(t), поэтому такие сигналы также называют противоположными.
Квадрат расстояния между сигнальными точками (эквивалентную энергию) определим в виде
|
T |
|
|
d 2 (S0 (t), S1 (t)) = EЭ = S0 (t) − S1 (t) 2 dt = S1 (t) = −S0 (t) = |
|
||
|
0 |
(14) |
|
T |
T |
||
|
|||
= S0 (t) + S0 (t) 2 dt = 4 S02 (t)dt = 4E |
|
||
0 |
0 |
|
|
Векторное представление сигналов с ФМ.
Из всех рассмотренных сигналов фазомодулированные сигналы имеют большее расстояние между концами векторов в векторном пространстве, поэтому, естественно ожидать, что они будут наиболее различимыми, а следовательно, самыми помехоустойчивыми.
Вероятность ошибки фазомодулированного сигнала равна
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
4E |
|
|
|
|
|
|
||
|
Э |
|
|
= 1 − F ( 2h2 ) |
|
||||||||||
PФМ |
= 1 − F |
|
|
|
= 1 − F |
|
|
|
(15) |
||||||
2N0 |
2N0 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||