- •Оуд.04 Математика
- •40.02.01 Право и организация социального обеспечения
- •1. Пояснительная записка
- •2. Паспорт фонда оценочных средств
- •2. Результаты освоения учебной дисциплины, подлежащие проверке
- •3. Контрольно-оценочные средства текущего контроля
- •3.1. Оценочные средства и критерии оценивания результатов обучения на лабораторно-практических занятиях Практическая работа «Развитие понятия о числе»
- •1 Вариант
- •Практическая работа «Развитие понятия о числе»
- •2 Вариант
- •Критерии оценки практическойой работы
- •Шкала перевода баллов в отметки
- •Ответы к практической работе «Развитие понятия о числе»
- •Практическая работа «Корни, степени и логарифмы»
- •1 Вариант
- •Практическая работа «Корни, степени и логарифмы»
- •2 Вариант
- •Критерии оценки практической работы
- •Шкала перевода баллов в отметки
- •Ответы к практической работе «Корни, степени и логарифмы»
- •Практическая работа «Прямые и плоскости в пространстве».
- •1 Вариант Уровень а.
- •Уровень в.
- •Уровень в.
- •Уровень с.
- •Критерии оценки практической работы
- •Шкала перевода баллов в отметки
- •Ответы к практической работе «Прямые и плоскости в пространстве».
- •Раздел 4. Комбинаторика Характеристика основных видов учебной деятельности студента (на уровне учебных действий): у1, у2, у7, з1, з2 Практическая работа «Комбинаторика».
- •Вариант
- •Практическая работа «Комбинаторика».
- •Вариант
- •Критерии оценки практической работы
- •Ответы к практической работе «Комбинаторика».
- •Шкала перевода баллов в отметки
- •Ответы к практической работе «Координаты и векторы».
- •Практическая работа «Основы тригонометрии».
- •1 Вариант
- •Практическая работа «Основы тригонометрии».
- •2 Вариант
- •Критерии оценки практической работы
- •Шкала перевода баллов в отметки
- •Ответы к практической работе «Основы тригонометрии».
- •Практическая работа «Функции и графики».
- •1 Вариант
- •Практическая работа «Функции и графики».
- •2 Вариант
- •Критерии оценки практической работы
- •Шкала перевода баллов в отметки
- •Ответы к практической работе «Функции и графики».
- •Практическая работа «Многогранники и круглые тела».
- •1 Вариант Уровень а.
- •Уровень в.
- •Уровень в.
- •Уровень с.
- •Критерии оценки практической работы
- •Шкала перевода баллов в отметки
- •Ответы к практической работе «Многогранники и круглые тела».
- •Практическая работа «Начала математического анализа».
- •1 Вариант Уровень а.
- •Уровень в.
- •Уровень с.
- •Критерии оценки практической работы
- •Шкала перевода баллов в отметки
- •Ответы к практической работе «Начала математического анализа».
- •Практическая работа «Интеграл и его применение».
- •1 Вариант Уровень а.
- •Уровень в.
- •Уровень с.
- •Критерии оценки практической работы
- •Шкала перевода баллов в отметки
- •Ответы к практической работе «Интеграл и его применение».
- •3.2. Оценочные средства и критерии оценивания результатов самостоятельной работы
- •4.1. Контрольно-оценочные средства промежуточной аттестации
- •При выполнении заданий 8-12 укажите ход решения и запишите полученный ответ.
- •При выполнении заданий 13-18 запишите ход решения и полученный ответ.
- •При выполнении заданий 8-12 укажите ход решения и запишите полученный ответ.
- •При выполнении заданий 13 - 18 запишите ход решения и полученный ответ.
- •При выполнении заданий 13-18 запишите ход решения и полученный ответ.
- •Дополнительная часть При выполнении заданий 19 - 22 запишите ход решения и полученный ответ.
- •При выполнении заданий 13 - 18 запишите ход решения и полученный ответ.
- •Дополнительная часть При выполнении заданий 19 - 22 запишите ход решения и полученный ответ.
- •Ответы к экзаменационной работе
- •Шкала перевода баллов в отметки по пятибалльной системе
- •5 Перечень оценочных средств и критериев оценивания результатов обучения по учебной дисциплине
Практическая работа «Функции и графики».
2 Вариант
А1.
Какой из
графиков, изображенных на рисунках 1) –
4), задает функцию?

А) 1). Б) 2). В) 3). Г) 4).
А2.
Найдите область определения функции
![]()
А) x > 3; Б) x < 3; В) x ≥ 3; Г) x < 1/3.
А3. По графику функции y = f(x) укажите: а) область определения функции; б) нули функции; в) промежутки постоянного знака функции; г) точки максимума и минимума функции; д) промежутки монотонности; е) наибольшее и наименьшее значения функции; ж) область значений функции. |
|
А4. Среди заданных функций укажите нечетные.
1)
у = 2х2;
2) у =
![]() ; 3) у = 5х.
; 3) у = 5х.
А) 1) и 3); Б) 2) ; В) 2) и 3); Г) 3) .
В.
Найдите область определения функции
у =
![]() .
.
С. Постройте график функции y = x2 – 2x + 1 и укажите ее свойства.
Критерии оценки практической работы
Задания |
Баллы |
Примечание |
А1 – А4 |
10 |
Каждый правильный ответ 1 балл |
В |
2 |
Каждый правильный ответ 2 балла |
С |
3 |
Каждый правильный ответ 3 балла |
Максимальный балл за работу – 15 баллов
Шкала перевода баллов в отметки
Отметка |
Число баллов, необходимое для получения отметки |
« 5» (отлично) |
15 - 14 |
« 4» (хорошо) |
13 - 12 |
« 3» (удовлетворительно) |
11 - 10 |
« 2 « (неудовлетворительно) |
менее 10 |
Ответы к практической работе «Функции и графики».
-
1 Вариант
2 Вариант
А1
В) 3
А)1
А2
В) x ≥
Б) x < 3
А3
а)
 ;
б)-2; 4; в) у > 0 при
;
б)-2; 4; в) у > 0 при
 ;
у < 0 при
;
у < 0 при
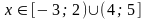 ;
;г)хmax = 0,2; xmin = 1; д) ф
 при
при
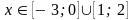 ;
ф
;
ф
 при
при
 ;
;е) унаиб = 6; у наим = - 1;
ж)
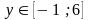 ;
;а)
 ;
б)-2; 1; в) у > 0 при
;
б)-2; 1; в) у > 0 при
 ;
у < 0 при
;
у < 0 при
 ;
;г)хmax = 2; xmin = - 1; д) ф при
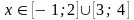 ;
ф
при
;
ф
при
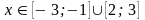 ;
;е) унаиб = 2; у наим = - 3;
ж)
 ;
;А4
Б) 1
В) 2) и 3)
В
х
 ;
х
;
х ;
;х ; х
 ;
;С
y = x2 – 4x + 3 = (х – 2)2 – 1
1)
 R;
2)
R;
2)
 ;
3) функция общего вида; 4) у > 0 при
;
3) функция общего вида; 4) у > 0 при
 ;
у < 0 при
;
у < 0 при
 ;
5) ф
при
;
5) ф
при
 ;
ф
при
;
ф
при
 ;
;y = x2 – 2x + 1 = (х – 1)2
1) R; 2)
 ;
3) функция общего вида; 4) у > 0 при
всех х
кроме 1; 5) ф
при
;
3) функция общего вида; 4) у > 0 при
всех х
кроме 1; 5) ф
при
 ;
;
ф при
 ;
;