Отчет Телесный угол
.docxБЕЛОРУССКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ АВИАЦИИ
Факультет гражданской авиации
Кафедра естественнонаучных и общепрофессиональных дисциплин
ОТЧЕТ
по самостоятельной работе по теме
«Телесный угол»
по дисциплине физика
СОДЕРЖАНИЕ
Введение……………………………………………………………………………...31. Понятие телесного угла………………………...………………………………....4
Задача…………………………………………………………………………………6
Выводы…………………………………………………………………………….....7
Литература………………………………………………………………………........8
Введение
Телесный угол — часть пространства, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую поверхность (которая называется поверхностью, стягивающей данный телесный угол). Частными случаями телесного угла являются трёхгранные и многогранные углы. Границей телесного угла является некоторая коническая поверхность. Обозначается телесный угол обычно буквой Ω.
Телесный угол измеряется отношением площади той части сферы с центром в вершине угла, которая вырезается этим телесным углом, к квадрату радиуса сферы:
.
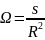(1)
Единицей измерения телесного угла в
системе СИ является стерадиан, равный
телесному углу, вырезающему из сферы
радиуса
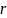поверхность с площадью
.
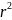1. Понятие телесного угла
При
измерении угла между двумя лучами на
плоскости удобно рассматривать данный
угол как центральный угол некоторой
дуги окружности единичного радиуса.
Тогда длина этой дуги и дает радианную
меру центрального угла. Полный угол
получает при этом меру, равную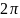 
.
Нечто сходное приходится проделывать,
когда мы хотим ввести меру объемного,
телесного угла, то есть меру, показывающую
«широту раствора» конической поверхности,
долю пространства, которое попадает
внутрь такой поверхности, по сравнению
с полным пространством (полным телесным
углом).
При этом совсем не обязательно данный угол заключать в круговой конус: это может быть любой конус, или угол может быть многогранным (Рисунок 1). Для введения строгого понятия телесного угла возьмем сферу единичного радиуса с центром в вершине угла (Рисунок 2).
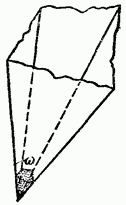
Рисунок 1 – Многогранный угол
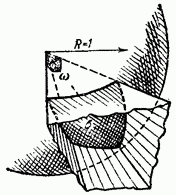
Рисунок 2 – Сфера единичного радиуса с центром в вершине угла
За
меру телесного угла принимается площадь
части поверхности сферы, лежащей внутри
данного угла. Полный телесный угол
измеряется всей площадью поверхности сферы,
то есть за его меру принимается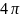 
. Единицей
телесного угла служит стерадиан
Задача
Найти
телесный угол, ограниченный конусом
вращения с углом при вершине осевого
сечения, равным
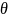(Рисунок 3).
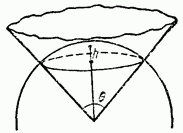
Рисунок 3 – Сфера
Решение
Проведем сферу единичного радиуса с центром в вершине конуса. Задача сводится к вычислению площади шапочки этой поверхности, лежащей внутри конической поверхности. Находим высоту стрелки соответствующего сегмента сферы:
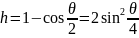
Площадь
искомой поверхности равна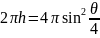 
.
Итак, телесный угол при вершине конуса
измеряется числом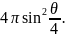 
Если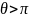 
,
то формула дает меру внешнего телесного
угла. При 
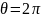получим
полный телесный угол (внешний угол по
отношению к конусу, превратившемуся в
луч).
Выводы
Таким образом, чтобы измерить телесный угол, надо: 1) мысленно начертить сферу радиуса R с центром в вершине телесного угла; 2) найти площадь поверхности Ds, которую вырежет на сфере телесный угол; 3) вычислить телесный угол по формуле
Телесные углы нашли практическое применение в:
Определении силы света и яркости и соответствующих радиометрических величин интенсивности излучения и яркости
Расчете сферического избытка сферического треугольника
Расчете потенциалов с использованием метода граничных элементов
Расчете электрического поля и напряженности магнитного поля вокруг зарядовых распределений
Получении Закона Гаусса
Расчете мощности излучения и излучения при теплопередаче
Расчете сечений в резерфордском рассеянии
Расчете сечений в комбинационном рассеянии
Литература
1. Сканави, М. И. Элементарная математика / М. И. Сканави. – 2-е изд. – Москва: Издательство «Наука» Главная редакция физико-математической литературы, 1974. – 592 с.
2. Китайгородский, А. И. Введение в физику / А. И. Китайгородский. – 1-е изд. – Москва: Издательство «Наука» Главная редакция физико-математической литературы, 1973. – 684 с.