4 4. Фнч Баттерворта. Порядок фильтра. Нормирование частоты.

Фильтр с рабочим ослаблением вида

где — коэффициент неравномерности в ПП;

— нормированная частота;

n — порядок фильтра,

называется фильтром с характеристикой Батерворта (с максимально плоской характеристикой) л-го порядка.

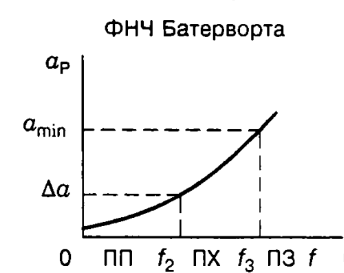
Фильтр Батерворта имеет монотонно возрастающую (максимально плоскую) характеристику. При нулевой частоте рабочее ослабление равно нулю.

Порядок фильтра определяется числом реактивных компонентов (катушек индуктивности и конденсаторов) в его схеме. Для ФНЧ Баттерворта порядок фильтра влияет на крутую характеристику затухания в полосе подавления. Чем выше порядок фильтра, тем круче будет переходная область между полосой пропускания и полосой подавления.

Нормирование – у разных фильтров различны значения элементов и граничных частот. Поэтому удобно провести нормирование. Вместо абсолютных значений сопротивлений элемента фильтра использовать их относительные величины, отнесенные к сопротивлению нагрузку Rн.

4 5. Фнч Чебышева. Порядок фильтра. Нормирование частоты.

Фильтр с рабочим ослаблением вида

где — многочлен Чебышева п-го порядка, называется фильтром с характеристикой Чебышева или с равномерно-колебательной характеристикой n-го порядка.

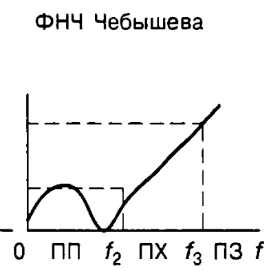
Фильтр Чебышева имеет равномерно-колебательную характеристику в полосе пропускания и монотонное возрастание в полосе задерживания. При нулевой частоте рабочее ослабление необязательно равно нулю.

Порядок фильтра Чебышева определяется так же, как и у других фильтров, числом реактивных компонентов в его схеме. Порядок фильтра влияет на крутизну переходной характеристики:

• Чем выше порядок фильтра, тем круче переходная характеристика.

• У фильтра Чебышева I типа крутизна спада выше, чем у эквивалентного фильтра Баттерворта того же порядка, но с пульсациями в полосе пропускания.

Нормирование – у разных фильтров различны значения элементов и граничных частот. Поэтому удобно провести нормирование. Вместо абсолютных значений сопротивлений элемента фильтра использовать их относительные величины, отнесенные к сопротивлению нагрузку Rн.

46. Аналоговые и дискретные сигналы. Теорема Котельникова.

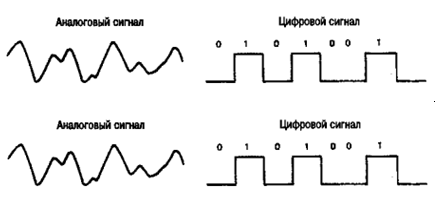
Дискретный сигнал - сигнал, имеющий конечное число значений.

Обычно сигналы, передаваемые через дискретные каналы, имеют два или три значения. Использование сигналов с тремя значениями обеспечивает синхронизацию передачи.

Аналоговый сигнал - сигнал, величина которого непрерывно изменяется во времени. Аналоговый сигнал обеспечивает передачу данных путем непрерывного изменения во времени амплитуды, частоты либо фазы.

Аналоговые сигналы естественным образом передают речь, музыку и изображения.

Теорема Котельникова, также известная как теорема выборки или теорема Найквиста-Шеннона, является основным принципом в теории дискретизации сигналов. Она утверждает, что для того чтобы избежать искажений при дискретизации аналогового сигнала, его частота дискретизации должна быть не меньше удвоенной частоты максимальной частоты сигнала, которую мы хотим зафиксировать.

Принцип теоремы Котельникова базируется на идее, что чтобы полностью описать быстро меняющийся сигнал, необходимо собирать данные о его состоянии с достаточной частотой. Если частота дискретизации слишком низкая, то это может привести к потере информации и искажению сигнала при его последующем восстановлении.