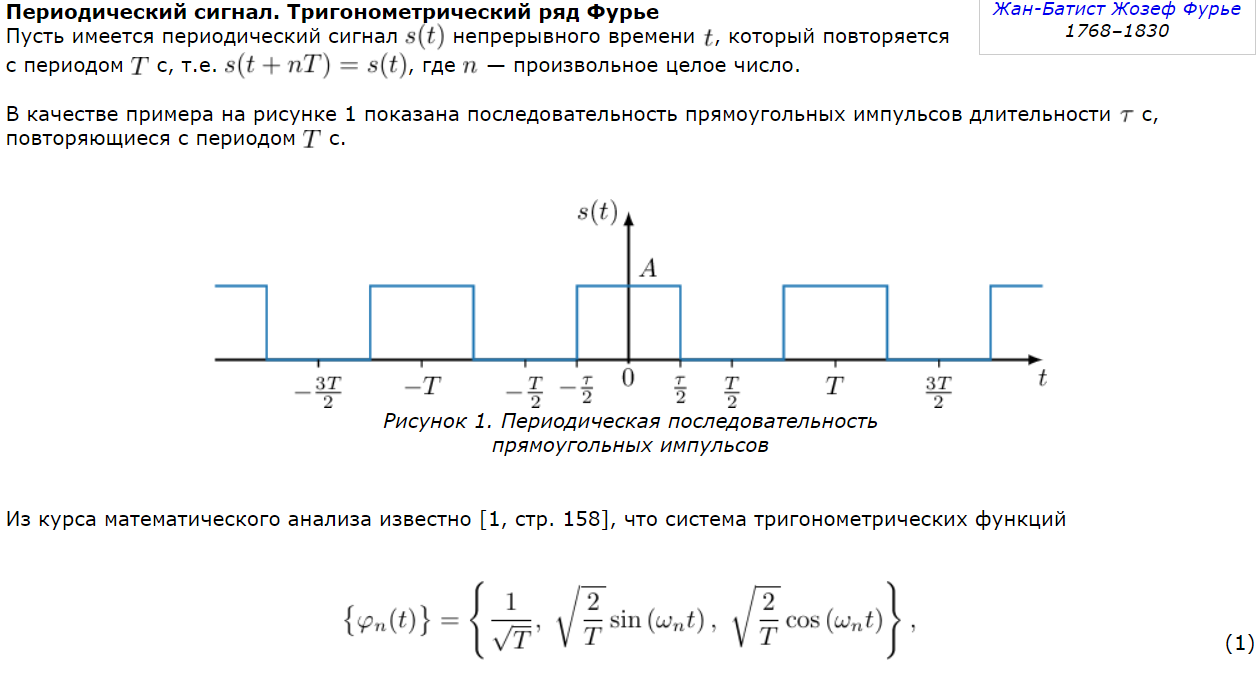
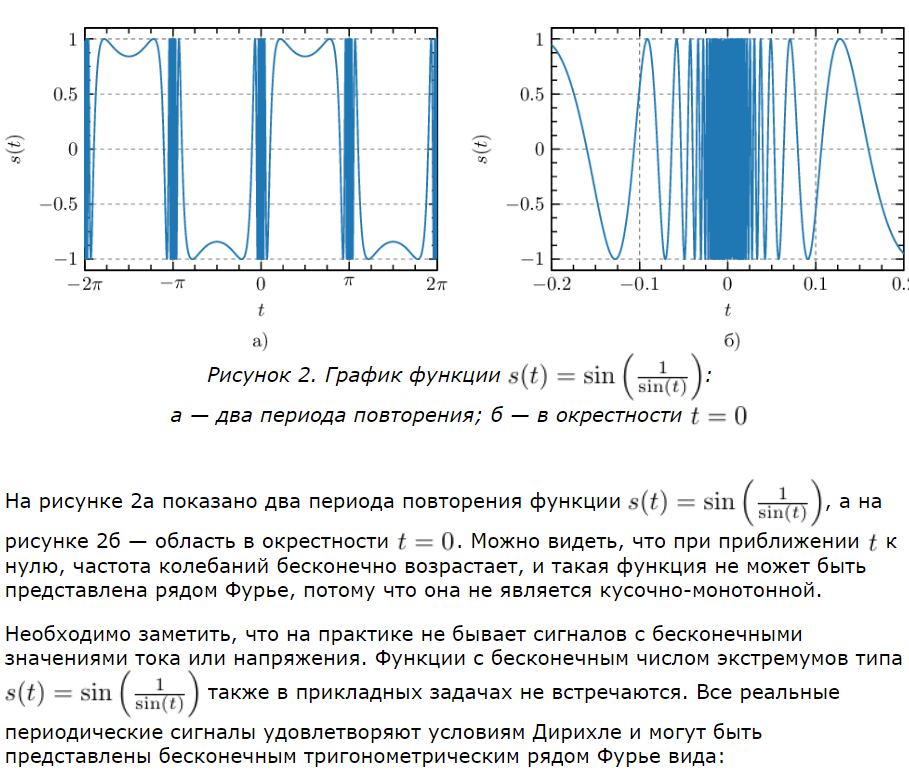
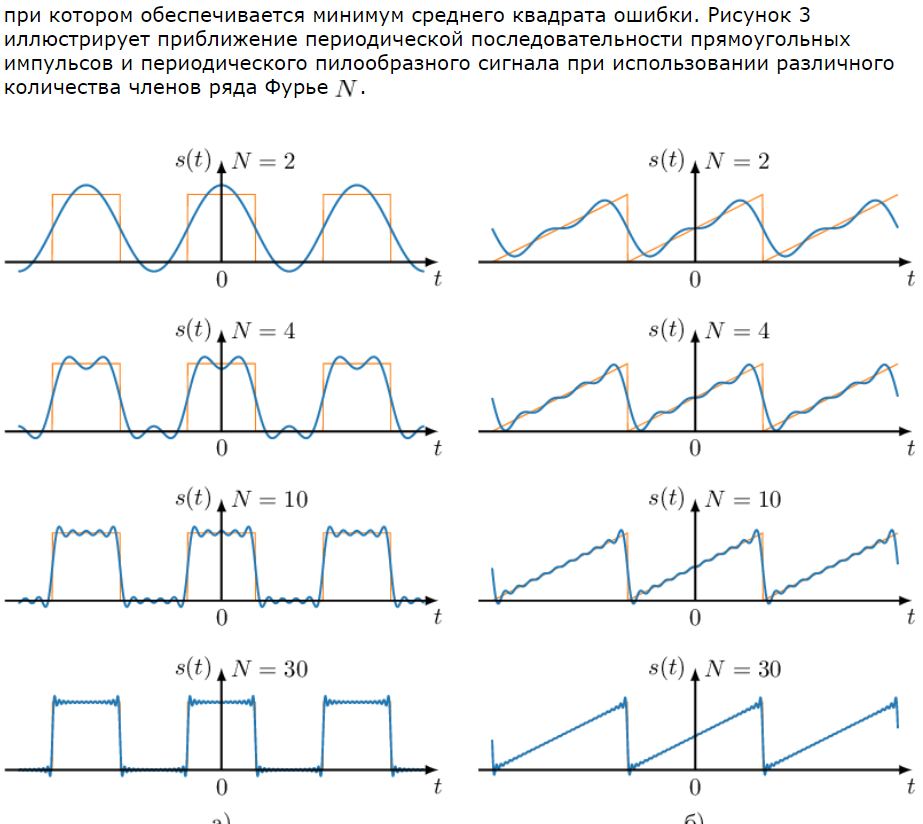
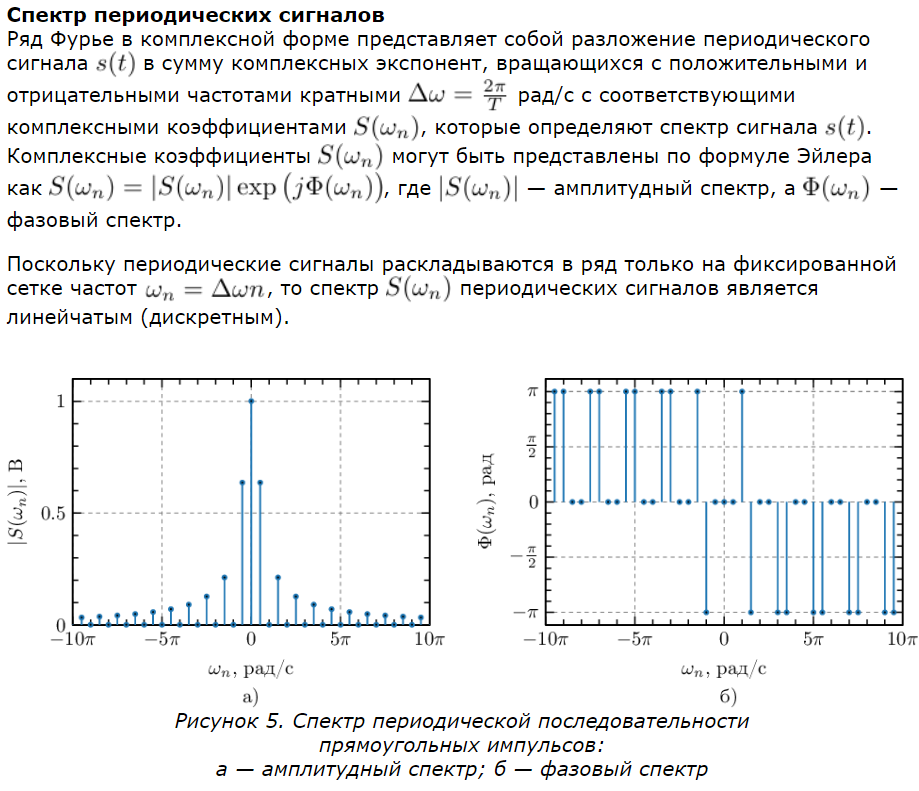
29. Ряд Фурье

30. Преобразование Фурье. Теорема запаздывания.

Преобразование Фурье

Преобразование Фурье — это математический метод, который позволяет разложить сложный сигнал (например, звуковую волну или электрический сигнал) на набор простых синусоидальных волн (синусоиды). Представьте себе музыкальную ноту. Преобразование Фурье позволяет нам увидеть эти отдельные волны.

Теорема запаздывания

Теорема запаздывания (также известная как теорема о временном сдвиге) говорит нам о том, как сдвиг сигнала во времени влияет на его представление в частотной области.

Если на вход линии подать синусоидальный сигнал, то на выходе будет наблюдаться запаздывание сигнала. Время запаздывания зависит от длины линии и фазовой скорости распространения волны в линии

31. Преобразование Фурье. Теорема масштабирования.

32. Преобразование Фурье. Фильтрующее свойство дельта-функции.

33. Спектральная плотность прямоугольного импульса.

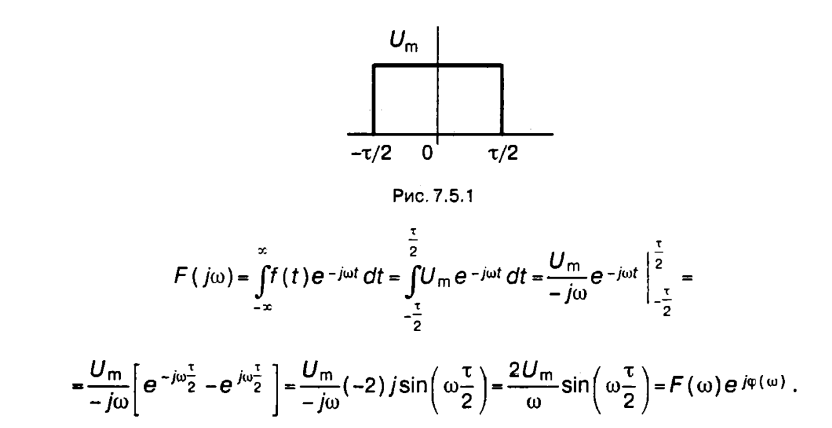
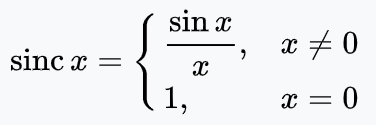
34. Связь между частотными и временными характеристиками.

Связь между частотными и временными характеристиками

Частотные и временные характеристики описывают поведение электрических цепей и систем во временной и частотной областях. Понимание связи между ними позволяет анализировать и проектировать системы, используя как временные, так и частотные методы.

Временные характеристики

Временные характеристики описывают, как система реагирует на входные сигналы во времени. К ним относятся:

• Переходная характеристика: Отклик системы на ступенчатый входной сигнал.

• Импульсная характеристика: Отклик системы на дельта-функцию (единичный импульс).

Частотные характеристики

Частотные характеристики описывают, как система реагирует на синусоидальные входные сигналы различных частот. К ним относятся:

• АЧХ (Амплитудно-частотная характеристика): Зависимость амплитуды выходного сигнала от частоты входного сигнала.

• ФЧХ (Фазо-частотная характеристика): Зависимость фазы выходного сигнала от частоты входного сигнала.

Преобразование Фурье

Преобразование Фурье — это математический инструмент, позволяющий переходить между временной и частотной областями. Оно преобразует временной сигнал в его частотное представление:

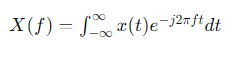
Обратное преобразование Фурье позволяет восстановить временной сигнал из частотного:

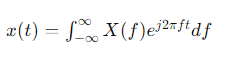
Импульсная и частотная характеристики

Импульсная характеристика h(t) и частотная характеристика связаны через преобразование Фурье:

Связь между временными и частотными характеристиками

1. Импульсная характеристика и частотный отклик: Импульсная характеристика системы h(t) является обратным преобразованием Фурье частотной характеристики . Таким образом, зная одну из характеристик, можно найти другую.

2. Переходная характеристика и частотный отклик: Переходная характеристика g(t), которая является откликом системы на единичный скачок, связана с импульсной характеристикой через интеграл:

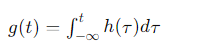
3. Связь через передаточную функцию: Передаточная функция H(s) (в комплексной плоскости s) описывает связь между входным и выходным сигналами в частотной области и является преобразованием Лапласа импульсной характеристики:

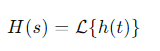
Временной и частотный анализ

• Временной анализ: Используется для изучения временных характеристик сигналов и систем, таких как переходные процессы и отклики на различные входные воздействия.

• Частотный анализ: Используется для изучения частотных характеристик систем, таких как фильтрация и резонанс.

Пример: RC-цепь

Рассмотрим простую RC-цепь (резистор и конденсатор в последовательности) и проанализируем её временные и частотные характеристики.

Временная характеристика

Импульсная характеристика RC-цепи:

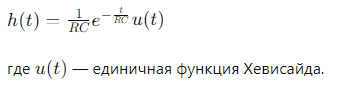
Частотная характеристика

Частотная характеристика (передаточная функция) RC-цепи:

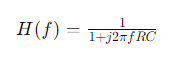
Связь

Используя преобразование Фурье, мы можем показать, что является преобразованием Фурье h(t).

Итоги

Связь между временными и частотными характеристиками играет ключевую роль в анализе и проектировании систем. Преобразование Фурье и преобразование Лапласа позволяют перейти от временной области к частотной и обратно, предоставляя мощные инструменты для понимания и управления динамическими системами.