Вантажознавство і технологія вантажних операцій. МВ до практичних занять

20

Рис. 1. Розташування вантажів на піддонах

Наприклад, піддон П4В краще, ніж 2П2В тому що 4 + 4 6 (рис. 1,б). Якщо кількість nР однакова, то вибір типа піддона – на розсуд студента. Наприклад, піддон П4В та 2П2В однакові тому що 6 + 6 = 12 (рис. 1,а). Далі розраховуємо розміри вантажу на піддоні, м

Якщо значення ℓГ або bГ близьке до габаритних розмірів піддона (пакета), то розгляд подальших варіантів не потрібен.

Якщо значення ℓГ або bГ менше відповідних розмірів піддона, то розглядаються інші варіанти просторового розміщення вантажу на піддоні. Деякі з можливих варіантів розміщення вантажів представлені на рис. 2.

Рис. 2. Схеми розміщення прямокутних вантажів на піддоні

Таким чином знаходиться такий варіант розміщення, який мінімізує порожнє місце на піддоні (див. друге правило пакетування на піддоні). Для перевірки можливості такого розміщення підсумовується довжина (ℓМ) і ширина (bМ) ВМ (декілька ℓМ або bМ) і ця величина порівняється з відповідними припустимими розмірами пакета.

21

Розглянемо розміщення вантажів циліндричної форми.

На піддони вантажі у формі циліндра встановлюються вертикально (на торець), і при їхньому розміщенні частина габаритних розмірів окремих ВМ може перекривати один одного (рис. 3, а).

Рис. 3. Схеми розміщення циліндричних вантажів на піддоні

Розраховуємо значення nℓ, nb, ℓГ і bГ.

При кратності розмірів піддона та вантажів (дробові частини nℓ і nb дуже близькі або дорівнюють цілій частині) проблем не виникає, і циліндричні вантажі розміщаються так само як прямокутні (рис. 3,б). При такому розміщенні габаритні розміри окремих ВМ не перетинаються. Для забезпечення рівномірності завантаження піддона частина вантажу може зміщатися в протилежні сторони або розташовується діагонально (рис. 3,в).

Коли на піддоні залишається досить багато вільного місця (ℓГ або bГ менше розмірів піддона), то розглядається інша схема розташування. При цьому габаритні розміри ВМ будуть перетинатися. При перетинанні габаритних об'ємів окремих ВМ, габаритні розміри вантажу на піддоні (ℓГ або bГ) тим менші, чим більше відстань між двома поруч розташованими ВМ (рис. 3,г). При цьому можливі різні варіанти взаємного розташування та кількості ВМ на піддоні (рис. 3,д).

Більше точним, але трудомістким методом розміщення в цьому випадку є геометричні побудови з використанням креслярських інструментів (циркуля, трикутника й ін.). Тоді в масштабі рисується прямокутник відповідного розміру (1300 900 мм і 1700 1300 мм). Від кутів до центра здійснюється розміщення ВМ шляхом побудови кіл відповідного радіуса, який визначається діаметром ВМ та обраним масштабом.

22

У роботі можна скористатися наближеним методом. Для цього використовується наступні залежності, які взаємно виключать одне інше (або перше або друге):

при щільному розташуванні ВМ першого ряду друг до друга та розміщенні другого ряду в поглиблення першого без зміни довжини, загальна ширина складе приблизно 0,85 максимальної ширини;

при розташуванні рядів вантажів так, щоб ширина пакета не змінювалася, загальна довжина складе приблизно 0,9 максимальної.

Тоді розміри вантажу на піддоні складуть, м

ℓ Г = 0,9 ℓМ n ℓ або b Г = 0,85 bМ n b,

де n ℓ і n b – відповідно можливе число ВМ за довжиною та шириною. Якщо отримане значення ℓ Г (b Г) не перевищує припустимого, то

Якщо отримане значення ℓ Г (b Г) більше припустимого, то відповідне значення n ℓ (n b) зменшується і розрахунок повторюється.

Знайшовши для кожного варіанта (вантажу) оптимальне розміщення його на піддоні та обрав тип піддона, визначаємо кількість ВМ у першому (нижньому) шарі (ярусі) вантажу nP (од.) і габаритні розміри пакета в плані ℓП bП

(м).

Розмір пакета (ℓП bП) дорівнює габаритному розміру піддона, якщо вантаж на піддоні не виступає за крайки піддона (менше піддона), наприклад ℓП bП = 1,6 1,2 м.

Якщо вантаж виступає (більше піддона), то габаритний розмір пакета дорівнює габаритному розміру вантажу, наприклад ℓП bП = 1,68 1,3 м.

У роботі приводяться всі схеми формування пакетів, із вказівкою значен-

ня nР (див. рис. 1, 2, 3).

Далі розраховуємо для кожного вантажу, за чергою, число шарів вантажу в пакеті за висотою.

Для цього визначаємо число шарів (рядів) за висотою, виходячи з максимальної маси пакета nh , од.

nh = (GMAX – gПОД) / (gМ nР).

З урахуванням максимально припустимої висоті пакета, визначаємо число шарів (рядів) за висотою nh , од.

nh = (HMAX – hПОД) / hМ.

Значення nh і nh дорівнюють цілій частини результату ділення, тому що число шарів не може бути дробовим.

Обмежувати висоту може nh або nh , або обидва одночасно, тоді шукане число шарів (рядів) за висотою пакета nh, од.

nh = min {nh ; nh }.

Габаритну висоту пакета hП (м) визначаємо з виразу hП = nh hМ + hПОД.

23

Практична робота № 4. Визначення кількості навалочного вантажу в штабелях правильної геометричної форми

Мета роботи. Вивчення практичних методів визначення кількості навалочного вантажу в штабелях правильної геометричної форми.

Загальні вказівки. Навалочні вантажі зберігаються в штабелях різної геометричної форми, але найпоширеніші штабелі правильної геометричної форми.

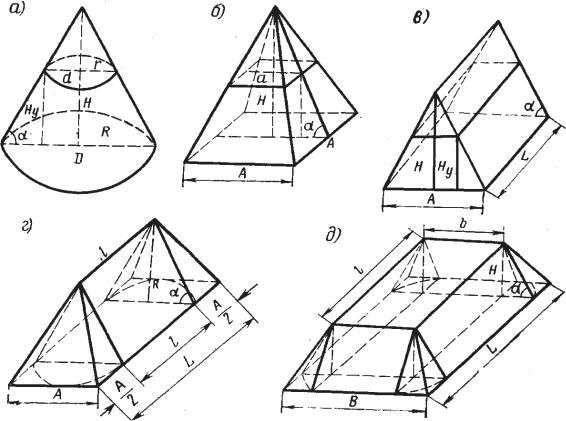
На рис. 1 представлений зовнішній вигляд штабелів навалочних вантажів у вигляді правильних геометричних фігур: конус (а), піраміда (б), призма (в), клин (г), обеліск (д).

Рис. 1. Види штабелів навалочних вантажів

Всі штабелі, крім призми та обеліска виходять при вільному відсипанні вантажу. Призма утворюється при формуванні штабеля між двома вертикальними стінками. Обеліск являє собою усічений клин і штабель у вигляді обеліска формують при обмеженні висоти складування вантажу. Обмеження висоти складування може бути обумовлено технічними можливостями складських площ (навантаженням) і перевантажувального встаткування й (або) транспортними характеристиками вантажу.

Конус, піраміда та призма є елементарним геометричними фігурами, а клин і обеліск – складеними.

Об'єм конуса, якщо відомий діаметр, визначається з виразу

VК = 1/12 D2 H,

24

але на практиці визначення діаметра конуса (D) і його висоти (H) здійснити важко, а часто-густо – неможливо. Найменшу складність представляє вимір довжини окружності основи конуса (S). Перетворивши формулу визначення довжини окружності S = D, одержимо D = S / .

Висота конуса визначається з виразу

H = D tg / 2,

виразивши діаметр D через довжину окружності S одержимо

H = S tg / (2 ).

Підставивши у формулу визначення VК значення D і H, які виражені через S і зробивши перетворення одержимо

VК = 1 / (24 2) S 3 tg = 0,00423 S 3 tg .

Об'єм піраміди визначається з виразу

VП = 1/3 A2 H.

Висоту піраміди H можна визначити через сторону основи за наступною формулою

H = A tg / 2.

Підставивши значення H у формулу визначення VП і провівши перетворення одержимо

VП = 1/6 A3 tg .

Об'єм призми визначається з виразу

VПР = 1/2 A H L.

Висоту призми H можна визначити через сторону основи за формулою аналогічній визначенню H піраміди.

Підставивши значення H у формулу визначення VПР і провівши перетворення одержимо

VПР = 1/4 A2 tg L.

Об'єм клина визначається як сума об'ємів призми (довжиною ℓ та шириною А) і піраміди зі стороною основи А (рис. 1, г). Обеліск визначається як сума об'ємів паралелепіпеда (довжиною ℓ, шириною b та висотою H), двох призм (шириною А, одною довжиною ℓ, інша довжиною b) і піраміди зі стороною основи А (рис. 1, д).

На практиці розміри основи клина (довжину L та ширину A) і обеліска (довжину L та ширину B) визначають безпосередніми вимірами. Визначення висоти обеліска H не представляє складності, тому що вона заздалегідь відома, так як відсипання (формування штабеля) здійснювалися на цю висоту. Визначення ж значень верхніх основ ℓ і b представляє певну складність.

Розглянемо спочатку штабель навалочного вантажу у вигляді клина. Клином називається п'ятигранник, основа якого – прямокутник, бічні грані – рівнобедрені трикутники та рівнобедрені трапеції.

На рис. 2 представлений зовнішній вигляд такого штабеля, позначений на рисунку буквами ABCD складений із клина BCFE і двох половин піраміди ABE

та CDF.

Скористаємося елементарними геометричними побудовами та принципом дзеркальної подоби. З рис. 2 видно, що половина піраміди ABE дорівнює ABE ,

27

При завантаженні транспортних засобів, часто встає питання про кількість вантажу яка знаходиться в порту. Тобто виникає необхідність рішення питання про те, чи необхідно або ні завозити додатково в порт вантаж для забезпечення повного завантаження транспортних засобів.

У порту вихідні дані для розрахунків одержують шляхом виміру рулеткою розмірів основи штабелів, кутоміром – кута природного укосу . Насипна маса ( ) визначається за нормативними документами або за допомогою мірного ящика. Потім, за отриманими даними, визначається об'єм штабеля VШТ і, використовуючи насипну масу , розраховується кількість вантажу QШТ.

Об'єм штабеля правильної геометричної форми можна визначити за допомогою номограми або розрахунковим способом, з використанням відомих у геометрії формул.

Номограма (рис. 5) дозволяє швидко, просто та з достатньою точністю визначати об'єми геометричних тіл правильної форми. Номограма складається з 9 логарифмічних шкал, розташованих на 5 осях:

перша шкала – діаметр конуса; довжина сторони піраміди; ширина призми (клина) – позначається 1 і А;

друга шкала – довжина окружності конуса – позначається 2 і S;третя шкала – об'єм піраміди – позначається 3 і VП;

четверта шкала – об'єм конуса – позначається 4 і VК;п'ята шкала – площа перетину призми – позначається 5 і С;шоста шкала – об'єм призми – позначається 6 і VПР;сьома шкала – висота штабеля – позначається 7 і Н;

восьма шкала – довжина призми та тангенс кута природного укосу – позначається 8, L і tg ;

дев'ята шкала – кут природного укосу – позначається 9 і .

Лінія, проведена через дві точки на двох будь-яких осях, дає можливість визначити всі інші елементи.

Коли значення вихідних даних більше ніж на шкалах 1, 2 і 7 то вони зменшуються в 10 разів, а результат (об'єм) збільшується в 1000 (103) разів.

Виключення становить призма, при зменшенні в 10 разів на шкалі 1, а об'єм збільшується в 100 (102) разів.

Це пояснюється тим, що об'єм виходить не відразу, а через проміжний результат С (площу). Якщо вихідні дані більше ніж на шкалі 8, вони зменшуються в 10 або 100 разів, а результат (об'єм) збільшується у відповідну кількість разів.

Принципи зменшення та збільшення можна сформулювати так:

якщо зменшувалася одновимірна величина (довжина) на шкалі 1, 2 і 7, а отримується відразу тривимірна величина (об'єм), то об'єм штабеля збільшується на коефіцієнт зменшення (число) у третьому ступені;

якщо зменшувалася одновимірна величина на шкалі 1 і 7, а отримується відразу проміжна двовимірна величина (площа), то об'єм штабеля збільшується на коефіцієнт зменшення в другому ступені;

якщо зменшувалася одновимірна величина на шкалі 8, то об'єм штабеля (інша величина) збільшується на цей коефіцієнт зменшення.

29

Такі принципи можна застосовувати і при зменшенні значень на шкалах 1, 2, 7 і 8 на інше значення, але при цьому розрахунки значно ускладнюється. Так, наприклад, при зменшенні довжини А за шкалою 1 в 3 рази отримані об'є- ми необхідно збільшити в 32 = 9 і 33 = 27 разів, що подумки провести складно, в порівнянні із збільшенням в 102 = 100 і 103 = 1000 разів.

У роботі окремо для кожного виду штабеля при визначенні за номограмою приводиться:

назва виду штабеля; необхідні для розрахунку вихідні дані;

значення, яке зняте з номограми, коефіцієнт збільшення (якщо він потрібний), підсумковий результат (об'єм);

всі проміжні значення, які зняті з номограми (якщо вони є). Наприклад. Конус. S = 40 м, = 35 , VК = 190 м3.

Піраміда. А = 25 м, = 35 , VП = 1,75 103 = 1750 м3.

Призма. А = 28 м, L = 40, = 35 , С = 1,35, VПР = 0,52 102 100 = 5200 м3.

Значення з номограми знімаються з максимально можливою точністю. Розрахунковий метод більше точний, але вимагає складних (із застосу-

ванням обчислювальної техніки) і трудомістких розрахунків та знання формул розрахунку об'ємів геометричних фігур.

У роботі окремо для кожного виду штабеля при визначенні розрахунковим методом приводиться:

назва виду штабеля; необхідні для розрахунку вихідні дані;

підсумкова розрахункова формула та результат (об'єм).

Значення тангенса кута природного укосу знімаються зі шкали 8 напроти значення шкали 9 з максимальною точністю.

Порядок виконання роботи. Відповідно до заданого варіанта визначаємо з табл. 1 шифри та кути природного укосу ( ) штабелів.

Таблиця 1

За обраним шифром штабелів з табл. 2 визначаємо їх найменування (вид), лінійні розміри та насипну масу.

Спочатку визначаємо об'єми штабелів за допомогою номограми.

Конус. Відкладаємо S на шкалі 2 (рис. 5) і на шкалі 9, з'єднуємо прямою лінією (лінійкою або іншим рівним предметом) ці точки. На перетинанні цієї