АиГ шаблон оформления ИДЗ

_{МИНОБРНАУКИ РОССИИ}

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра алгоритмической математики

отчет (образец)

по индивидуальному домашнему заданию № 1

по дисциплине «Алгебра и геометрия»

Тема: многочлены и комплексные числа

Студент__ гр. ____		Фамилия И.О.
Преподаватель		Абросимов И.К.

Санкт-Петербург

2020

ВАРИАНТ ЗАДАНИЯ¹ И ОТВЕТЫ К ЗАДАЧАМ

Примечания будут записываться красным. В окончательном варианте Вашего отчета их (включая данное) быть не должно!

Рисунок 1 – Вариант задач ИДЗ

Таблица 1. Ответы к задачам

№	Ответ
1	решений нет при , решений бесконечное множество при , единственное решение имеет вид .
22	.3
3	.

РЕШЕНИЕ ЗАДАЧ ИДЗ

Задача № 1.⁴

При каких значениях параметра уравнение^{5 6} не имеет решений? Имеет бесконечно много решений? Имеет единственное решение? Найдите его.

Дано:⁷

;⁸

;

.

Решение.

У уравнения нет решений, тогда и только тогда, когда и одновременно. Решим уравнения и .

;

;

;

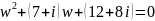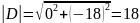; ⁹

¹⁰

Аналогично расписывается решение уравнения (Вам расписывать его нужно).

;

<…>¹¹

Таким образом, , и при уравнение не имеет решений.

У уравнения бесконечно много решений тогда и только тогда, когда . Учитывая, что ¹² уравнение имеет бесконечно много решений при .

Пусть и , тогда уравнение преобразуется к , это и есть корень исходного уравнения.

Ответ: решений нет при , решений бесконечное множество при , единственное решение имеет вид .

Задача № 2.

Решить в тригонометрической форме и записать ответ в алгебраической .

Дано:

;

.

Решение.

;

;

;

; ¹³

;

<…>

Задача № 3.

Разложить на множители над множеством комплексных чисел .

Дано:

.

Решение.

;

Найдем с помощью компьютера НОД и , после чего найдем нули найденного многочлена:

;

<…>

.

Таким образом, найдены два корня, кратности 1. Следовательно, они же являются корнями кратности 2. Выполним последовательное (дважды) деление на , а затем – на :

;

;

;

;

<…>

1

Для вставки своего варианта используйте инструмент «Ножницы» или его аналог.

2

Ответ к задаче 2 может оказаться слишком длинным для строки. В этом случае следует разбить множество корней на два множества, объединенных знаком (управляющая последовательность , после нажатия пробела сразу за ней заменится на символ ), например:

Было:

Стало:

3

Корни произвольной степени можно ввести при помощи конструктора редактора формул (раздел «радикалы»); квадратный корень вводится при помощи управляющей последовательности (УП)

4

Для переписывания задачи с варианта удобно использовать инструмент «Разделить страницу» на вкладке «Вид» основной ленты Word.

5

Чтобы вставить окончание строки без окончания абзаца, следует использовать сочетание клавиш < Shift > + < Enter > (вместо < Enter > для окончания абзаца).

6

Если скобки в формуле введены правильно, то их размер автоматически станет корректным (внутренние – самые маленькие, обрамляющие их – больше), если нажать на пробел после них (не выходя из формулы); степень вводится при помощи символа «крышка» («^»), например после нажатия пробела без выхода из формулы превращается в ; нижний индекс вводится при помощи нижнего подчеркивания («_»)

7

Раздел «Дано» не обязателен и введен для удобства

8

В конце каждой формулы, стоящей в отдельном абзаце, ставится «;» либо «.», причем эти символы ставится сразу за формулой, в формулу они не входят

9

Чтобы ввести функцию, которая не считается стандартной в Word, Вам следует ввести в формуле и нажать пробел: в результате получится , после этого Вы сможете заменить обозначение синуса на любое требуемое, например 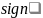(не забудьте после этого ввести аргумент функции вместо квадратика).

10

В случае, когда формула заканчивается скобами, каждая строка отделяется запятой, точке с запятой (либо точка) ставится в последней строке а сразу после формулы ставится пробел

11

Знаком <…> обозначены места, которые Вам уже известно, как оформлять

12

При разрыве формулы на две строки знак равенства ставится в конце старой строки и в начале новой, абзац при этом не разрывается (т.е. в конце строки вводится окончание строки без окончания абзаца)

13

Греческие буквы вводятся при помощи УП ( ), ( ), …, ( )