3. Начальная выставка

Особенностью алгоритмов определения параметров ориентации и навигации, построенных на использовании показаний инерциальных датчиков, является необходимость ввода начальных значений углов ориентации, проекций линейных скоростей и координат. Скорость и координаты могут быть получены, например, с приёмника ГНСС. Углы ориентации определяются в процессе начальной выставки [6]. Важно отметить, что, в большинстве случаев, начальная выставка осуществляется по углам крена и тангажа, ввиду большой погрешности определения курса. В ПАО МКНС начальная выставка обеспечивает определение углов крена и тангажа, а угол курса может быть получен от магнитометра или приёмника ГНСС.

В этой работе рассматривается два метода осуществления начальной выставки: метод векторного согласования и использование алгоритма гировертиакли.

Сущность метода векторного согласования состоит в том, что взаимная ориентация двух координатных базисов всегда может быть определена, если в осях этих базисов определены две естественно существующие или искусственно созданные неколлинеарные векторные величины.

При решении задачи начальной выставки методом векторного согласования используются два векторных параметра, измеряемых ИИМ – вектор абсолютной угловой скорости вращения объекта и вектор его кажущегося ускорения.

 

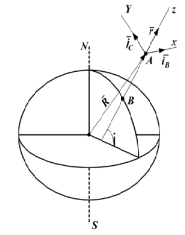
Рисунок 5 – Направление векторов для алгоритма начальной выставки

 

Пусть в качестве базового трехгранника используется стартовая система координат осей, положение которой показано на рисунке 5 географическим базисом . Взаимное положение навигационного трехгранника этого базиса и базиса  , связанного с объектом, определяется матрицей направляющих косинусов [С] (6):

 

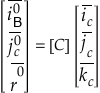
(6)

 

Алгоритм вычисления этой матрицы можно построить на основе измерений двух векторных параметров – вектор абсолютной угловой скорости вращения объекта, равного угловой скорости вращения Земли 𝑢, и вектор ускорения свободного падения 𝑔. Составляющие этих векторов в осях стартового трехгранника известны априори, а в осях базиса они могут быть непосредственно измерены БИНС.

В Дополнительно следует ввести вектор 𝜈̅, ортогональный векторам  и (7):

 

𝜈̅ = ×

(7)

 

Связь между проекциями этих векторов на оси базисов можно представить в виде:

 

[ ; ;   ] = 𝐶0[  ;  ; ]

(8)

где 𝐶⁰ – начальное значение матрицы направляющих косинусов [С].

Из соотношения (8) следует: 

[𝐶0] = [  ; ] −1 ×[  ; ].

(9)

где  – вектор проекций ускорение свободного падения Земли;

 – вектор проекций угловых скоростей Земли;

 – показания акселерометров;

 – показания ДУС;

 

Матрица направляющих косинусов [C⁰], соответствует начальному положению ИИМ в пространстве. Эта матрица поступает на вход алгоритма БИНС при переходе ПАО МКНС от режима «Начальная выставка» к режиму «Навигация».

Ограничением этого алгоритма является требование сохранения неподвижного положения объекта на всем протяжении выполнения начальной выставки. 

Начальная выставка с применением алгоритма гировертикали основывается на том, что показания гировертикали сходятся к истинным значениям крена и тангажа при неподвижном положении объекта. Алгоритм гировертикали запускается с нулевыми начальными значениями углов курса, крена и тангажа. Далее, на протяжении заданного времени, выполняется алгоритм гировертикали, описанный в первом промежуточном отчете [1]. Так как алгоритм гировертикали не вычисляет курс, в алгоритм вводятся показания магнитометра или курс, полученный по показаниям приёмника ГНСС.

В таблице 2 приведены входные и выходные данные алгоритма начальной выставки.

 

Таблица 2 – Входные и выходные параметры алгоритма начальной выставки

№	Входные параметры	Выходные параметры
	Показания ДУС	Матрица направляющих косинусов [C] размерности (3,3)
	Показания акселерометров
	Широта, высота

 

Для рассмотренных методов, входная и выходная информация совпадает.

Начальная выставка методом векторного согласования наиболее распространена в высокоточных системах, так как ошибки датчиков навигационного класса имеют значительно меньшие величины по сравнению с измеряемыми векторами силы тяжести и угловой скорости вращения Земли. Точность автономной выставки также зависит от широты места, в котором осуществляется выставка. Наибольшую точность метод векторного согласования имеет при нулевой широте (на экваторе) и не применим при широте  (на полюсах). Метод начальной выставки, построенный на алгоритме гировертикали менее точен, но более устойчив к погрешностям инерциальных датчиков, что особенно важно для МЭМС.