сд5

Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

КИБЭВС

БИНАРНЫЕ ДЕРЕВЬЯ ПОИСКА Отчет по практической работе №5 по дисциплине «Структуры данных»

Студент гр. 713-1

_______ В.С.Колосова

_______

Принял:

преподаватель КИБЭВС

_______ Е.Е. Лунёва

_______

Томск 2024

Задание

Реализовать бинарное дерево поиска при помощи динамических структур

(классы). Предусмотреть следующие интерфейсные методы:

•Инициализация пустого дерева;

•Добавление элемента в дерево bool AddItem(int a) - возвращает true, если добавление прошло успешно, иначе false. Например, если такой элемент уже был в дереве - то метод вернет false;

•Удаление элемента из дерева bool RemoveItem(int a);

•Очистка дерева void Clear();

•Вывод дерева (используйте поиск в ширину) void Print() или string Print();

Вариант 8. Реализуйте метод, находящий самый большой и самый

маленький элемент в дереве.

2

3

1 Введение

Целью работы является реализация бинарного дерева поиска при помощи

динамических структур (классы). Предусмотреть следующие интерфейсные

методы:

•Инициализация пустого дерева;

•Добавление элемента в дерево bool AddItem(int a) - возвращает true, если добавление прошло успешно, иначе false. Например, если такой элемент уже был в дереве - то метод вернет false;

•Удаление элемента из дерева bool RemoveItem(int a);

•Очистка дерева void Clear();

•Вывод дерева (используйте поиск в ширину) void Print() или string Print();

Вариант 8. Реализуйте метод, находящий самый большой и самый маленький элемент в дереве.

4

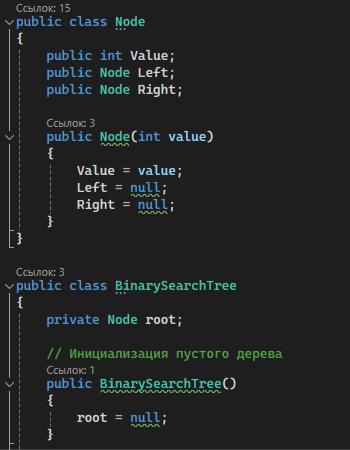
2 Ход работы

Реализовано два класса и инициализация бинарного дерева поиска

(рисунок 2.1). Класс Node хранит в себе данные текущего узла и ссылки на левое и правое поддерево. Класс Tree хранит в себе методы по заданию и инициализацию пустого бинарного дерева поиска c переменной корня дерева.

Рисунок 2.1 — Классы Node и Tree

Реализованы методы AddItem и AddItemRecursive в классе Tree, которые добавляют новый элемент в бинарное дерево поиска (рисунок 2.2). В методах предусмотрена проверка на пустое дерево и на существующий элемент в нём,

если проверка выполняется, то вернёт true и добавит элемент в дерево, иначе вернёт false. Рекурсивная функция определяет, куда добавить элемент.

5

удаляется согласно правилу. Если найден узел с двумя потомками, сначала ищется минимальное значение в правом поддереве и заменяет узел.

Рисунок 2.3 — Методы RemoveItem и RemoveItemRecursive в классе Tree

7

Реализован метод Clear, который полностью очищает дерево, в классе Tree (рисунок 2.4).

Рисунок 2.4 — Метод Clear в классе Tree

Реализован метод FindMin, который проходится по левому поддереву до его конца и таким образом не находит минимальное значение(рисунок 2.5).

Рисунок 2.5 — Метод FindMin в классе Tree

Реализован метод FindMin, который проходится по правому поддереву до его конца и таким образом не находит минимальное значение(рисунок 2.6).

Рисунок 2.6 — Метод FindMax в классе Tree

Реализован метод Print, который выводит элементы дерева по ширине, в

классе Tree (рисунок 2.7). В начале метода идёт проверка на наличие узлов.

8

Создаётся очередь, в которой хранятся узлы дерева. Цикл while, который добавляет дочерние узлы, работает до тех пор, пока индекс элемента очереди не достигнет количества элементов в очереди.

Рисунок 2.7 — Методе Print в классе Tree

При удалении элементов из бинарного дерева поиска наблюдается 3

случая:

1.У удаляемого элемента нет поддеревьев;

2.У удаляемого элемента есть одно поддерево;

9

3.У удаляемого элемента два поддерева.

Впервом случае, удаляемый элемент является «листом», поэтому он без проблем удаляется (рисунок 2.8).

Во втором случае, удаляемый элемент заменяется поддеревом –

«перевешивается» (рисунок 2.9).

В третьем случае необходимо найти наименьший элемент правого поддерева.

Если наименьший элемент является «листом», то используем первый случай.

Если наименьший элемент имеет поддерево, то используем «перевешивание»

(рисунок 2.10 – 2.11).

Рисунок 2.8 – Удаление листа

10