
сд2
.pdf
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра комплексной информационной безопасности электронно-
вычислительных систем (КИБЭВС)
АЛГОРИТМИЧЕСКАЯ СЛОЖНОСТЬ
Отчет по практической работе №2
по дисциплине «Структуры данных»
Студент гр. 713-1
Колосова В.С.
Руководитель преподаватель КИБЭВС
Лунёва Е.Е.
Томск 2024
|
|
Содержание |
1 |
Введение ..................................................................................................................... |
3 |
2 |
Ход работы ................................................................................................................. |
4 |
2.1 |
Сортировка расчёской ............................................................................................... |
4 |
2.2 |
Быстрая сортировка ................................................................................................... |
6 |
2.3 |
Сортировка Шелла..................................................................................................... |
8 |
2.4 |
Анализ таблицы ....................................................................................................... |
10 |
3 |
Заключение............................................................................................................... |
11 |
ПРИЛОЖЕНИЕ А.......................................................................................................... |
12 |
|
2
1 Введение
Цель работы: подсчитать время выполнения и количество операций при осуществлении сортировки расчёской, быстрой сортировки и сортировки Шелла, а также построить графики зависимости и оценить алгоритмическую сложность каждой сортировки. Листинг программы представлен в приложении А.
3
|
2 Ход работы |
|
|
2.1 Сортировка расчёской |
|
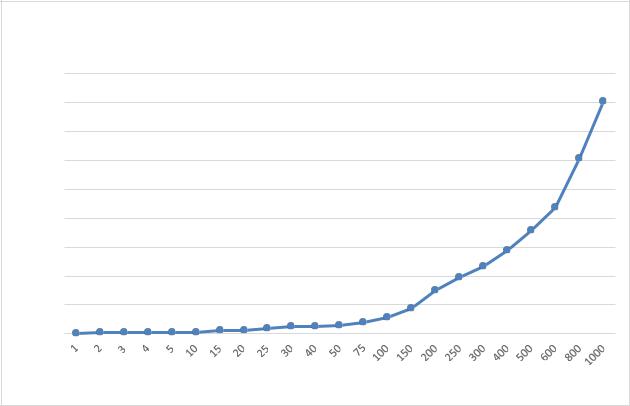
Для оценки алгоритмической сложности сортировки построим график |
||
зависимости времени от длины массива (рисунок 2.1) и график зависимости |
||
количества операций от длины массива (рисунок 2.2) |
||
|
Зависимость времени сортировки массива расчёской от |
|
|
длины массива |
|
|
1,8 |
|
|
1,6 |
|
|
1,4 |
|
|
1,2 |
|
мс |
1 |
|
Время, |
||
0,8 |
||
|
||
|
0,6 |
|
|
0,4 |
|
|
0,2 |
|
|
0 |
|
|
Количество элементов массива |
|
|
Рисунок 2.1 - График зависимости времени от размера массива |
|
4
|
Зависимость количества операций сортировки расчёской от |
|||
|
длины массива |
|
|
|
|
22000 |
|
|
|
|
17000 |
|
|
|
операций |
12000 |
|
|
|
|
|
|
|
|
Количество |
7000 |
|
|
|
|
|
|
|
|
|
2000 |
|
|
|
|
-3000 |
|
|
|
|
Количество элементов массива |
|
||
|
Сортировка n^2 |
n^3 |
n*log(n) |
n |
|
расческой |
|
|
|
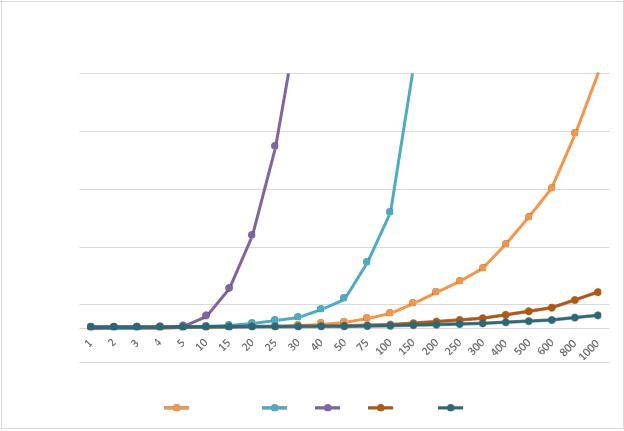
Рисунок 2.2 - График зависимости количества операций от размера массива |
||||
Как видно |
из рисунка |
2.2 график проходит между худшим случаем, |
|||
алгоритмическая |
сложность |
которого будет равной O(n2), и лучшем |
|||
O(n*log(n)). |
Это |
соответствует |
теоретическим |
данным. |
|
5
2.2 Быстрая сортировка |
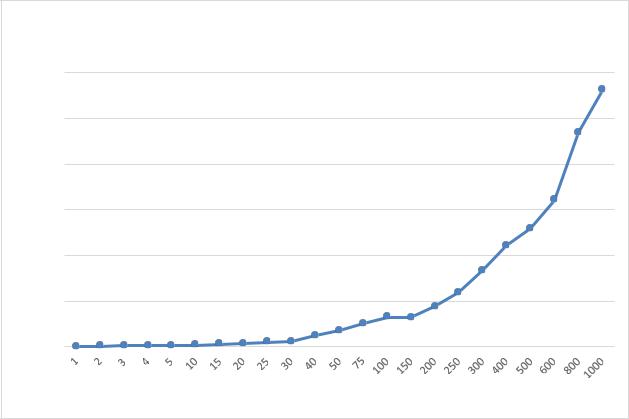
Для оценки алгоритмической сложности сортировки построим график |
зависимости времени от длины массива (рисунок 2.3) и график зависимости |
количества операций от длины массива (рисунок 2.4) |
Зависимость времени быстрой сортировки массива от длины |
массива |
3 |
2,5 |
2 |
мс |
1,5 |
Время, |
1 |
0,5 |
0 |
Количество элементов массива |
Рисунок 2.3 - График зависимости времени от размера массива |
6
|
Зависимость количества операций быстрой сортировки от |
||||
|
|
длины массива |
|
|
|
|
16000 |
|
|
|
|
|
14000 |
|
|
|
|
операций |
12000 |
|
|
|
|
10000 |
|
|
|
|
|
8000 |
|
|
|
|
|
Количество |
|
|
|
|
|
6000 |
|
|
|
|
|
4000 |
|
|
|
|
|
|
|
|
|
|
|
|
2000 |
|
|
|
|
|
0 |
|
|
|
|
|
|
Количество элементов массива |
|
||
|
Быстрая |
n^2 |
n^3 |
n*log(n) |
n |
|
сортировка |
||||
|
|
|
|
|
|
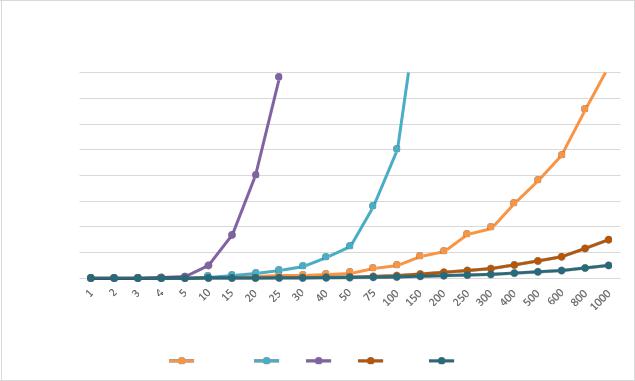
Рисунок 2.4 - График зависимости количества операций от размера массива. |
|||||
В быстрой сортировке при случайной генерации элементов массива график функции проходит между y=n2(худшим исходом) и y=n*log(n) (лучшим исходом). Таким образом, программа сгенерировала среднюю сложность массива, что отображается в среднем уровне производительности.
7
2.3 Сортировка Шелла |
Для оценки алгоритмической сложности сортировки построим график |
зависимости времени от длины массива (рисунок 2.5) и график зависимости |
количества операций от длины массива (рисунок 2.6) |
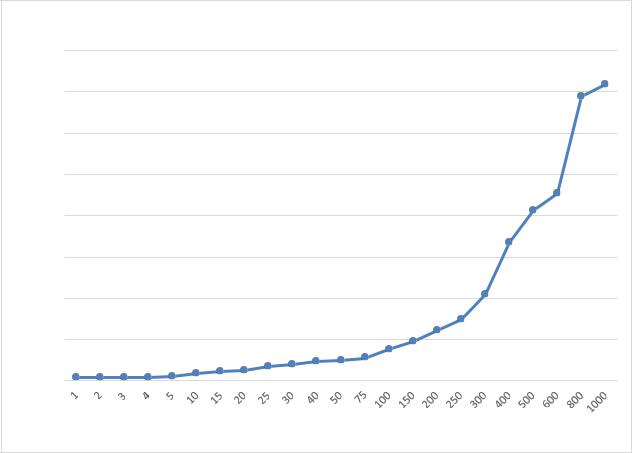
Зависимость времени сортировки Шелла от длины массива |
0,8 |
0,7 |
0,6 |
0,5 |
мс |
0,4 |
Время, |
0,3 |
0,2 |
0,1 |
0 |
Количество элементов массива |
Рисунок 2.5- График зависимости времени от размера массива |
8
|
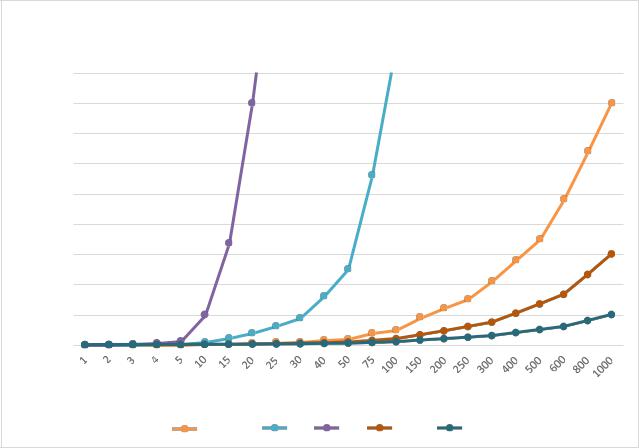
Зависимость количества операций сортировки Шелла от |
||||
|
|
длины массива |
|
|
|
|
9000 |
|
|
|
|
|
8000 |
|
|
|
|
|
7000 |
|
|
|
|
операций |
6000 |
|
|
|
|
5000 |
|
|
|
|
|
|
|
|
|
|
|
Количество |
4000 |
|
|
|
|
3000 |
|
|
|
|
|
|
|
|
|
|
|
|
2000 |
|
|
|
|
|
1000 |
|
|
|
|
|
0 |
|
|
|
|
|
|
Количество элементов массива |
|
||
|
Сортировка |
n^2 |
n^3 |
n*log(n) |
n |
|
Шелла |
||||
|
|
|
|
|
|
Рисунок 2.6 – График зависимости количества операций от размера массива |
|||||
В сортировке Шелла при случайной генерации элементов массива график функции проходит близко к y=n (лучшему исходу) и располагается достаточно далеко от y=n2 (худшего исхода). Сгенерированный вариант является усреднённым решением.
9
2.4 Анализ таблицы
Сравнение алгоритмов сортировки по времени и числу операций
приведены в таблице 2.4.1.
Таблица 2.4.1 - Сравнение сортировок
|
|
Сортировка расчёской |
Быстрая |
Сортировка |
||||
|
|
|
|
сортировка |
Шелла |
|
||
|
|
|
|
|
|
|
|
|
|
|
Худший |
Лучший |
Худший |
Лучший |
Худший |
|
Лучший |
№ |
|
|
|
|
|
|
|
|
|
|
случай |
случай |
случай |
случай |
случай |
|
случай |
|
|
|
|
|
|
|
|
|
1 |
Число операций |
1339 |
1233 |
9999 |
7499 |
503 |
|
503 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Время сортировки |
5,385 |
3,967 |
8,326 |
7,494 |
5,024 |
|
4,792 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число операций |
1339 |
1233 |
9999 |
7499 |
503 |
|
503 |
2 |
|
|
|
|
|
|
|
|
|
|
5,894 |
4,275 |
8,743 |
8,090 |
4,776 |
|
4,579 |
|
Время сортировки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число операций |
1339 |
1233 |
9999 |
7499 |
503 |
|
503 |
3 |
|
|
|
|
|
|
|
|
|
Время сортировки |
5,123 |
4,705 |
8,905 |
7,094 |
4,292 |
|
4,210 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число операций |
1339 |
1233 |
9999 |
7499 |
503 |
|
503 |
4 |
|
|
|
|
|
|
|
|
|
|
6,003 |
4,320 |
9,162 |
7,734 |
3,978 |
|
5,003 |
|
Время сортировки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число операций |
1339 |
1233 |
9999 |
7499 |
503 |
|
503 |
5 |
|
|
|
|
|
|
|
|
|
Время сортировки |
5,566 |
4,732 |
7,996 |
8,121 |
4,587 |
|
4,337 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5,594 |
4,400 |
8,626 |
7,707 |
4,531 |
|
4,584 |
|
Среднее время |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Согласно полученным экспериментальным данным, при реализации сортировок наиболее удачным выбором является сортировка Шелла.
10
