
чм3
.pdfМинистерство науки и высшего образования Российской Федерации Федеральное государственное автономное образовательное учреждение высшего образования
«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ» (ТУСУР)
Кафедра комплексной информационной безопасности электронновычислительных систем (КИБЭВС)
ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ ФУНКЦИИ В ТАБЛИЧНОМ И АНАЛИТИЧЕСКОМ ВИДЕ
Отчёт по лабораторной работе №3 по дисциплине «Численные методы»
Студент гр. 713-1
________ В.С. Колосова
________
Принял Старший преподаватель кафедры КИБЭВС
_________ Е.С. Катаева
________
Введение
Цели работы:
•построение квадратного интерполяционного полинома Лагранжа для последовательности точек и для функции в аналитическом виде;
•построение аппроксимирующей квадратной функции для последовательности точек и для функции в аналитическом виде;
•прогнозирование значения функции с помощью интерполирующей и аппроксимирующей функции;
•вычисление промежуточной точки с помощью интерполирующей и аппроксимирующей функции.
2 ХОД РАБОТЫ
2.1 Предварительный анализ данных
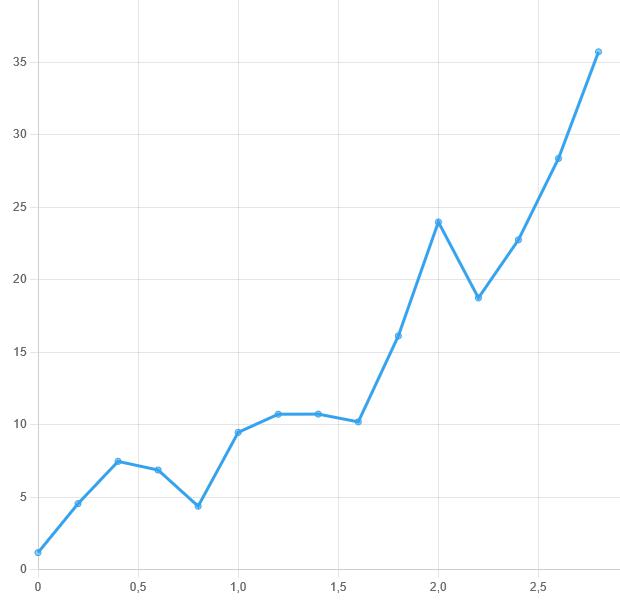
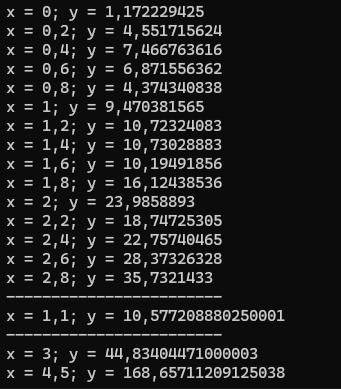
Был построен график по таблице значений из индивидуального задания.
Таблица значений представлена в таблице 2.1. График представлен на рисунке
2.1
Рисунок 2.1 – График
Таблица 2.1 – Последовательность точек
x |
y |
|
|
0.0 |
1.172229425 |
|
|
0.2 |
4.551715624 |
|
|
0.4 |
7.466763616 |
|
|
0.6 |
6.871556362 |
|
|
0.8 |
4.374340838 |
|
|
1.0 |
9.470381565 |
|
|
1.2 |
10.72324083 |
|
|
1.4 |
10.73028883 |
|
|
1.6 |
10.19491856 |
|
|
1.8 |
16.12438536 |
|
|
2.0 |
23.9858893 |
|
|
2.2 |
18.74725305 |
|
|
2.4 |
22.75740465 |
|
|
2.6 |
28.37326328 |
|
|
2.8 |
35.7321433 |
|
|
Были построены графики для функций y = ln(10,45x+0,1) и y = cos(6,98x + 1,56), графики представлены на рисунке 2.2 и рисунке 2.3 соответственно.
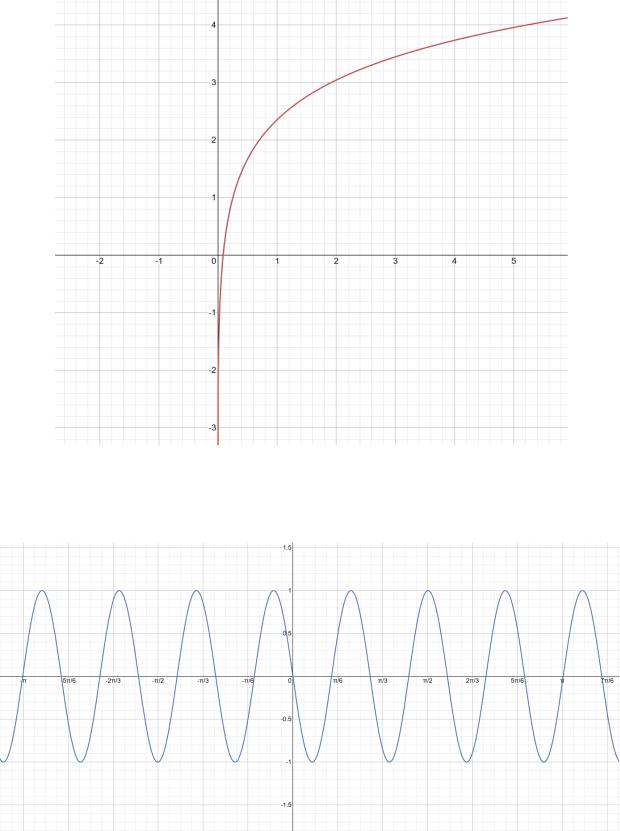
Рисунок 2.2 – График y = ln(10,45x+0,1)
Рисунок 2.3 – График y = cos(6,98x + 1,56)
Таблица 2.2 – Последовательность точек для y = ln(10,45x+0,1)
x |
y |
|
|
0.0 |
-2.302585093 |
|
|
0.2 |
0.783901544 |
|
|
0.4 |
1.453953010 |
|
|
0.6 |
1.851599470 |
|
|
0.8 |
2.135349174 |
|
|
1.0 |
2.356125860 |
|
|
1.2 |
2.536866389 |
|
|
1.4 |
2.689886230 |
|
|
1.6 |
2.822568655 |
|
|
1.8 |
2.939690883 |
|
|
2.0 |
3.044522438 |
|
|
2.2 |
3.139399623 |
|
|
2.4 |
3.226050029 |
|
|
2.6 |
3.305787197 |
|
|
2.8 |
3.379633204 |
|
|
Таблица 2.3 – Последовательность точек для y = cos(6,98x + 1,56)
x |
y |
|
|
0.0 |
0.010796117 |
|
|
0.2 |
-0.982827061 |
|
|
0.4 |
-0.352638252 |
|
|
0.6 |
0.860174137 |
|
|
0.8 |
0.651819843 |
|
|
1.0 |
-0.633461325 |
|
|
1.2 |
-0.872147284 |
|
|
1.4 |
0.330115293 |
|
|
1.6 |
0.986966382 |
|
|
1.8 |
0.013166561 |
|
|
2.0 |
-0.982386853 |
|
|
2.2 |
-0.354855585 |
|
|
2.4 |
0.858962707 |
|
|
2.6 |
0.653615822 |
|
|
2.8 |
-0.631625227 |
|
|
Для последовательностей, приведенных выше, были построены графики, представленные на рисунке 2.4 и рисунке 2.5 соответственно.
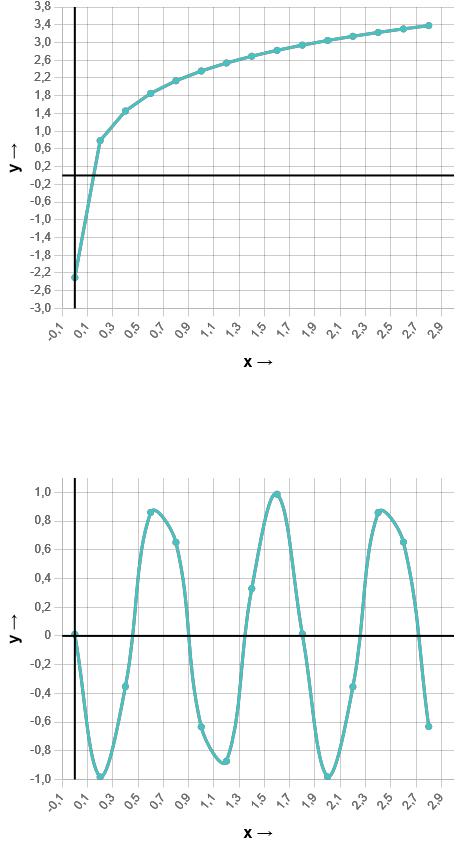
Рисунок 2.4 – График точек для y = ln(10,45x+0,1)
Рисунок 2.5 – График точек для y = cos(6,98x + 1,56)
Графики функций по заданным точкам совпадают с непрерывными графиками функций, следовательно, узловые точки заданы достаточно часто для качественного дальнейшего анализа.
2.2 Построение интерполяционного полинома Лагранжа
Для построения интерполяционного полинома Лагранжа была реализована программа, представленная в приложении А.
В основе программы лежит формула квадратичного полинома Лагранжа
(2.1):
2( ) = |
|
( − )( −( +1)) |
|
( −1) |
+ |
( −( −1))( −( +1)) |
|
+ |
|
( −( −1))( − ) |
|
|
( +1) |
(2.1) |
||||||||||||
( |
( −1) |
− |
)( |
( −1) |
− |
) |
( |
− |
( −1) |
)( − |
( +1) |
) |
( |
( +1) |
− |
( −1) |
)( |
− |
) |
|||||||
|
|
|
|
( +1) |
|
|
|
|
|
|
|
|
|
|
|
( +1) |
|
|
|
|
||||||
Для искомой точки x выбираются узлы, соответствующие условиям:
( −1) < ;
{( +1) > ;
( −1) < < ( +1)
Если х > xmax , то берутся последние три известные точки. Если x < xmin,
то берутся первые три известные точки.
На рисунках 2.6-2.8 представлены результаты работы программы для трех последовательностей точек.
Рисунок 2.6 – Результат работы программы для первой последовательности точек
