чм1

Введение

Целью лабораторной работы является написание программ для численного решения систем линейных алгебраических уравнений методом Зейделя и для численного решения нелинейного уравнения методом Ньютона и методом простых итераций.

2

ХОД РАБОТЫ

1 Численное решение систем линейных алгебраических уравнений

Преобразование систем уравнения к виду осуществляется следующим образом: сначала вычисляется сумма всех переменных уравнения, кроме переменной из главной диагонали, а затем из свободного члена вычитается полученная сумма. Это преобразование применяется ко всем уравнениям системы, обновляя значения переменных в процессе. Результат работы программы представлен на рисунке 1.1. Листинг программы представлен в приложении А, результаты работы программы представлены в таблице 1.1.

Рисунок 1.1 – Преобразование уравнения к виду метода Зейделя

Результат работы программы при решении индивидуальной системы уравнений представлен на рисунке 1.2.

Рисунок 1.2 – Результат работы программы при решении индивидуальной системы уравнений

3

Таблица 1.1 – Результаты работы программы

4

2 Численное решение нелинейного уравнения

Был проведен этап отделения корня для проверочного уравнения графическим способом, графики представлены на рисунках 2.1-2.2. Получены отрезки [-6,3; -3,5] и [0,2; 8,3].

Рисунок 2.1 – Графическое отделение корня для проверочного уравнения

Рисунок 2.2 – Графическое отделение корня для проверочного уравнения

5

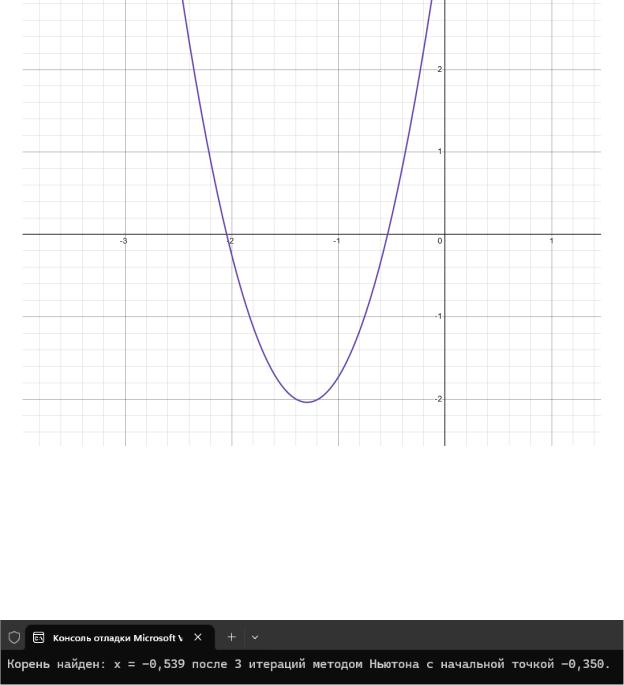
Был проведен этап отделения корня для проверочного уравнения графическим способом, график представлен на рисунке 2.3. Получены отрезки

[-3,9; -1,8] и [-1,1; 0,4].

Рисунок 2.3 – Графическое отделение корня для индивидуального уравнения

Результат работы программы при решении индивидуального уравнения методом Ньютона представлен на рисунке 2.4.

Рисунок 2.4 – Результат работы программы при решении индивидуального уравнения методом Ньютона

Листинг программы методом Ньютона, выполняющей уточнение корня

6

на найденном выше отрезке представлен в приложении Б.

Результат работы программы при решении индивидуального уравнения

методом простых итераций представлен на рисунке 2.5.

Рисунок 2.5 – Результат работы программы при решении индивидуального

уравнения методом простых итераций

Листинг программы методом простых итераций, выполняющей

уточнение корня на найденном выше отрезке представлен в приложении В.

Результаты программ представлены в таблицах 2.1-2.2.

Таблица 2.1 – Результаты работы программ для проверочного уравнения

Таблица 2.2 – Результаты работы программ для индивидуального уравнения

7

Заключение

В ходе лабораторной работы были написаны программы для численного решения систем линейных алгебраических уравнений методом Зейделя и для численного решения нелинейного уравнения методом Ньютона и методом простых итераций.

8

Приложение А

// матрица - левая часть уравнений double[,] left =

{

{-8.53, -1.0, 2.95 },

{4.41, -13.27, 7.54 },

{-6.87, -6.62, -17.6 }

}; // матрица - правая часть уравнений

double[] right =

{ 3.92, -1.16, 0.63 };

double[] answers = new double[right.Length]; //массив для решений x1, x2, x3 double error = 0.001; //погрешность

int counter = 0; //счетчик итераций

int max_iterations = 1000; //максимальное кол-во итераций bool flag = false; //проверка решения

for (int iteration = 0; iteration < max_iterations; iteration++)

{

double[] new_answers = (double[])answers.Clone(); //копия решения для сравнения

flag = true;

//цикл проходит по всем уравнениям

for (int i = 0; i < right.Length; i++) 9

{

double sum = 0;

//поиск суммы всех переменных уравнения, кроме текущей for (int j = 0; j < left.GetLength(1); j++)

{

if (j != i) //проверка переменной

{

sum += left[i, j] * answers[j];

}

}

//вычисление значения переменной answers[i] = (right[i] - sum) / left[i, i]; //проверка сходимости

if (Math.Abs(answers[i] - new_answers[i]) > error)

{

flag = false;

}

}

counter++;

if (flag) //если сошлось

{

Console.WriteLine($"Решение сошлось после {counter}

итераций");

10