Plasma / Secheniya / 2 - K

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра электронных приборов и устройств

отчет

по лабораторной работе №2

по дисциплине «Прикладная физика плазмы»

Тема: «ИССЛЕДОВАНИЕ МЕТОДИК РАСЧЕТА СЕЧЕНИЯ ИОНИЗАЦИИ АТОМОВ ПРИ СОУДАРЕНИИ ЭЛЕКТРОНОВ С АТОМОМ»

Студенты гр.		.
		Р.
		.
Преподаватель		Марцынюков С. А.

Санкт-Петербург

2024 г.

Цель работы: ознакомление с методикой расчета сечения ионизации атомов, усредненного по функциям распределения электронов по энергии, для различных условий газового разряда.

Основные теоретические положения.

1 -

-

1. Исходные данные

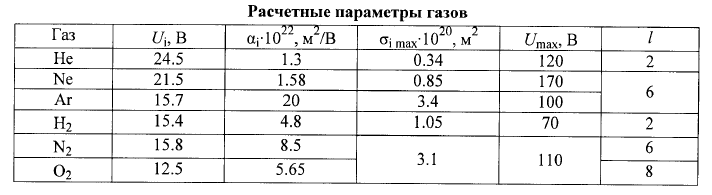Таблица 1 – Исходные данные для расчетов

2. Расчетные формулы:

При небольших энергиях электронов используется линейная аппроксимация:

(1)

где – коэффициент пропорциональности;

– энергия ионизирующих электронов;

– потенциал ионизации атома или молекулы.

В широком диапазоне энергий электронов можно применять следующие аппроксимации:

(2)

где ;

- потенциал ионизации атома водорода по Ридбергу;

– расчетные коэффициенты;

– число эквивалентных электронов на внешней оболочке ионизируемого атома.

аппроксимацию, приведенную в работе В. Л. Грановского:

(3)

где – максимальное значение сечения ионизации, которому соответствует энергия электронов .

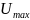3. Расчетные зависимости

• Зависимости были построены для газов Ne, O2 и H2. Представлены на рисунках 1, 2, 3 соответственно

50

σ_i, м²

10^-20

3*10^-20

2*10^-20

10^-22

U, В

Рисунок 3 – Зависимость для неона

10^-19

2*10^-20

71

4*10^-20

6*10^-20

8*10^-20

σ_i, м²

10^-22

U, В

Рисунок 4 – Зависимость для кислорода

σ_i, м²

5*10^-21

10^-20

1.5*10^-20

48

10^-22

U, В

Рисунок 5 – Зависимость для водорода

По полученным графикам определены диапазоны в которых можно использовать линейную аппроксимацию для неона – 0…50 эВ, для кислорода 0…71 эВ и для водорода 0…48 эВ.

• Зависимости распределения электронов по энергиям

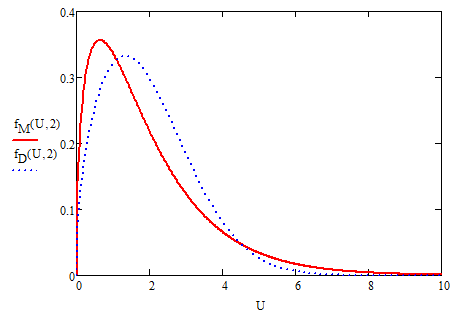
Рисунок 6 - Зависимости распределения электронов по энергиям для

2 эВ по Максвеллу f_M и Дрюйвестейну f_D

Рисунок 5 - Зависимости распределения электронов по энергиям для

4 эВ по Максвеллу f_M и Дрюйвестейну f_D

Рисунок 6 - Зависимости распределения электронов по энергиям для

6 эВ по Максвеллу f_M и Дрюйвестейну f_D

• Зависимости эффективного сечения ионизации от средней энергии электронов двух видов аппроксимаций и двух распределений по энергиям.

W, эВ

, м²

Рисунок 7 - Зависимости эффективного сечения ионизации неона от средней энергии электронов для аппроксимации Лотца–Дрэвина и двум распределениям по энергиям

W, эВ

, м²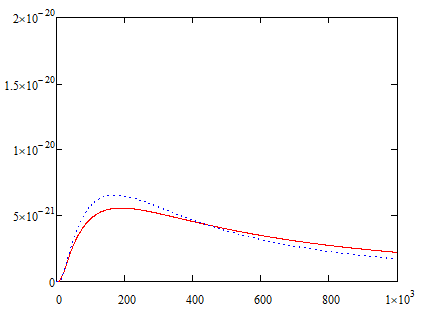

Рисунок 8 - Зависимости эффективного сечения ионизации неона от средней энергии электронов для аппроксимации Грановского и двум распределениям по энергиям

W, эВ

, м²

Рисунок 9 - Зависимости эффективного сечения ионизации водорода от средней энергии электронов для аппроксимации Лотца–Дрэвина и двум распределениям по энергиям

W, эВ

, м²

Рисунок 10 - Зависимости эффективного сечения ионизации неона от средней энергии электронов для аппроксимации Грановского и двум распределениям по энергиям

W, эВ

, м²

Рисунок 11 - Зависимости эффективного сечения ионизации кислорода от средней энергии электронов для аппроксимации Лотца–Дрэвина и двум распределениям по энергиям

W, эВ

, м²

Рисунок 12 - Зависимости эффективного сечения ионизации кислорода от средней энергии электронов для аппроксимации Грановского и двум распределениям по энергиям

• Исследование влияния ступенчатых процессов.

Первое приближение: U_{i cт} ≈ U_i/2

W, эВ

, м²

Рисунок 13 - Зависимости эффективного сечения ионизации неона от средней энергии электронов для аппроксимации Лотца–Дрэвина и двум распределениям по энергиям c учетом ступенчатых процессов

, м²

W, эВ

Рисунок 14 - Зависимости эффективного сечения ионизации неона от средней энергии электронов для аппроксимации Грановского и двум распределениям по энергиям с учетом ступенчатых процессов

Вывод

В результате выполнения данной работы были изучены особенности влияния различных условий газового разряда на сечение ионизации атомов. Зависимость сечения ионизации от энергии электронов были построены для 3 типов аппроксимаций, и было установлено, что линейная аппроксимация применима только для малых энергий порядка нескольких десятков эВ. Кроме того можно заметить, что аппроксимации Лотца–Дрэвина и Грановского схожи по своему характеру, то есть нелинейные и характерным максимумом, однако, максимум зависимости по Лотцу–Дрэвину выражен сильнее и находится ближе к потенциалу ионизации.

Так же было выполнено сравнение двух типов распределений электронов по энергиям. В результате можно сказать, что у распределения Дрюйвестейна наиболее вероятные энергии электронов, то есть максимум распределения смещен к более высоким энергиям по сравнению с распределением Максвелла. При сравнении функций распределения по средней энергии электронов, видно, что при увеличении средней энергии максимум распределения снижается, график становится более пологим и сдвигается в сторону больших энергий.

При расчете эффективного сечения ионизации было установлено, что для обоих видов аппроксимаций работающих в широком диапазоне энергий, расчет эффективного сечения ионизации по распределению Дрюйвестейна дает слегка завышенный результат в максимуме зависимости, так как распределение Дрюйвестейна используется в случае интенсивной ионизации.

Учет ступенчатых процессов на расчет эффективного сечения ионизации незначительно изменил лишь порядок величин, характер зависимостей не изменился.