Plasma / Dreif / 1

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра электронных приборов и устройств

отчет

по лабораторной работе №1

по дисциплине «Прикладная физика плазмы»

Тема: «РАСЧЕТ СКОРОСТИ ДРЕЙФА ЗАРЯЖЕННЫХ ЧАСТИЦ В ГАЗЕ ПОД ДЕЙСТВИЕМ ВНЕШНЕГО ЭЛЕКТРИЧЕСКОГО ПОЛЯ»

Студенты гр.		.
		.
		.
Преподаватель		Марцынюков С. А.

Санкт-Петербург

2024 г.

Цель работы: ознакомление со спецификой движения электронов и ионов в газе под действием электрического поля.

Основные теоретические положения.

Заряженные частицы (электроны и ионы), принимающие участие в электрическом токе в газе, находятся в состоянии непрерывного движения, определяемого направленной и хаотической составляющими. Направленная составляющая обусловлена действием внешнего электрического поля, устремляющего заряженную частицу к ускоряющему электроду (например, электрон к аноду). После столкновения с нейтральной частицей заряженная частица начинает двигаться в любом направлении, однако при этом становится возможным дрейф под действием внешнего электрического поля.

Рассмотрим движение электронов под действием электрического поля. Схематически (рис. 1) показан путь электрона среди группы атомов газа при наличии в разрядном промежутке однородного электрического поля напряженности Е. Непрерывное столкновение электрона, ускоряемого электрическим полем, с встречающимися на пути атомами газа приводит к тому, что электрон перемещается по сложным зигзагообразным путям.

Рисунок 1 - Путь электрона в газе при однородном электрическом поле

Характерным в таком движении является то, что электрон, двигаясь беспорядочно, сохраняет вместе с тем и некоторую составляющую скорости.

Как правило, дрейфовая составляющая скорости заряженной частицы гораздо меньше ее хаотической, что позволяет оценить ее среднюю на правленную скорость. При напряженности внешнего электрического поля E

Обработка результатов

1. Исходные данные

Таблица 1 – Исходные данные для расчетов

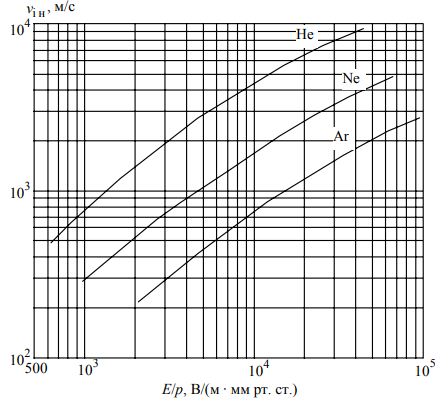
Рисунок 2 - Скорость дрейфа ионов в некоторых инертных газах

2. Расчетные формулы:

Дрейфовая скорость ионов (ν_iн) определяется как

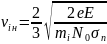(1)

где Е – напряженность внешнего электрического поля;

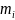– масса иона;

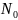– концентрация нейтральных частиц;

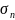– сечение перезарядки.

Сечение перезарядки определяется как

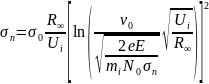(2)

где ;

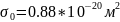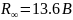- потенциал ионизации атома водорода по Ридбергу;

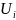– потенциал ионизации атома;

;

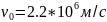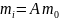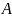( – атомная масса, 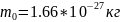– масса протона;

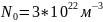- концентрация нейтралов при 1 мм рт. ст. и 300К

Дрейфовая скорость ионов используя понятие подвижности иона

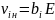(3)

где 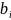– подвижность ионов.

3. Пример решения трансцендентного уравнения для Не

Для построения зависимости 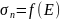для гелия выбирается диапазон напряженностей по рисунку 2, 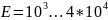В, фиксируем значение Е для нескольких точек и находим графически решая уравнение (2)

Рисунок 3 – Графическое решение для Е = 10³ В

Аналогичным образом находятся промежуточные значения для точности графика, затем таким же методом находятся значения для неона и аргона.

Зависимости для всех трех газов представлены на одном графике.

Е, В

He

Ne

Ar

σ_П, м²

3*10^-19

5*10^-19

4*10^-19

2*10^-19

1*10^-19

Рисунок 4 - Зависимость для гелия неона и аргона

Полученные значения сечений перезарядки для трех газов представлены в таблице 2.

Таблица 2 – Найденные значения сечений перезарядки для трех газов

He		Ne			Ar
σП * 1019, м2	Е, В		σП * 1019, м2	Е, В	σП * 1019, м2	Е, В
2.37	103		3.5	103	4.54	3*103
2.15	2*103		2.97	3*103	4.19	5*103
1.88	4*103		2.66	6*103	3.89	9*103
1.6	8*103		2.4	104	3.35	2*104
1.53	104		2.13	2*104	2.91	4*104
1.3	2*104		1.94	3*104	2.7	6*104
1.15	4*104		1.77	5*104	2.51	9*104

4. Расчет дрейфовой скорости ионов

Используя расчетные значения сечений перезарядки по формуле (1) находятся дрейфовые скорости ионов для соответствующих напряженностей и значения для линейной модели используя формулу (3). Экспериментальные значения определяются по графику на рисунке 2.

Результаты расчета сведены в таблицу 3

Пример расчета в программе

Таблица 3 – Экспериментальные, расчетные и линейные значения дрейфовых скоростей ионов

He			Ne				Ar
νi н (эксп), м/c	νi н (расч), м/c	νi н (лин), м/c		νi н (эксп), м/c	νi н (расч), м/c	νi н (лин), м/c	νi н (эксп), м/c	νi н (расч), м/c	νi н (лин), м/c
7.5*102	1.741*103	103		3*102	640	400	3*102	689	480
1.5*103	2.585*103	2*103		7.4*102	1.205*103	1.2*103	4.5*102	926	800
2.5*103	3.91*103	4*103		1.3*103	1.8*103	2.4*103	7*102	1.289*103	1.44*103
3.8*103	5.993*103	8*103		1.8*103	2.447*103	4*103	1.3*103	2.071*103	3.2*103
4.5*103	6.852*103	104		2.6*103	3.673*103	8*103	1.9*103	3.143*103	6.4*103
6.5*103	1.043*104	2*104		3.4*103	4.714*103	1.2*104	2.4*103	3.996*103	9.6*103
9*103	1.581*104	4*104		4.2*103	6.371*103	2*104	2.8*103	5.075*103	1.44*104

ν_{i н}, м/c

Сопоставление расчетной зависимости дрейфовой скорости ионов от напряженности электрического поля, экспериментальной и рассчитанной по формуле (3) линейной модели для каждого газа представлено на рисунках 5, 6 и 7

экспериментальная

линейная

расчетная

Е, В

Рисунок 5 – Сопоставление экспериментальных и теоретических зависимостей дрейфовой скорости для гелия (He)

ν_{i н}, м/c

расчетная

экспериментальная

линейная

Е, В

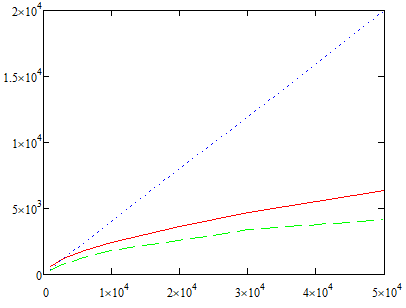
Рисунок 6 – Сопоставление экспериментальных и теоретических зависимостей дрейфовой скорости для неона (Ne)

линейная

Е, В

ν_{i н}, м/c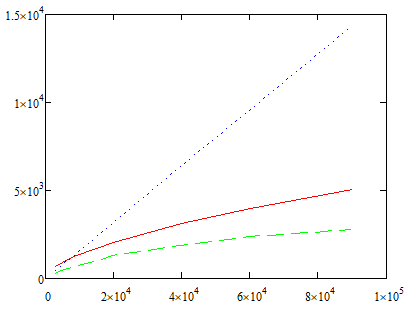

Рисунок 7 – Сопоставление экспериментальных и теоретических зависимостей дрейфовой скорости для аргона (Ar)

Вывод

В результате выполнения данной работы были изучены особенности движения заряженных частиц в газе под действием электрического поля. Дрейфовая скорость ионов была рассчитана путем решения трансцендентного уравнения графическим методом, затем была получена зависимость сечения перезарядки от напряженности и по значениям сечений перезарядки рассчитаны дрейфовые скорости.

Расчет дрейфовых скоростей по линейной модели осуществлялся используя понятие подвижности ионов.

При сравнении расчетных скоростей, экспериментальных и линейных можно сказать, что линейная зависимость дает завышенные результаты скоростей, расчетные и экспериментальные значения зависят от напряженности нелинейно и при росте напряженности возрастают медленно, это можно объяснить тем что, при расчете через подвижность не учитывается явление перезарядки ионов, т. е. для ионов характерно эстафетное перемещение, как следствие при росте напряженности дрейфовая скорость претерпевает рассеяние из-за чего замедляется ее рост пропорционально полю (при больших напряженностях ионы быстро ускоряются полем и быстро рассеивают приобретенный импульс соударяясь о нейтральный атом, который в свою очередь снова ускоряется полем и процесс повторяется, тем самым дрейфовая скорость не может быстро расти из-за постоянных рассеиваний на нейтральных частицах).