МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ТОР

отчет

по лабораторной работе №3

по дисциплине «Цифровая обработка сигналов»

Тема: Дискретное преобразование Фурье

Студенты гр. 1
Преподаватель		Апалина П.В.

Санкт-Петербург

2024

Цель работы:

• Расчет дискретного преобразования Фурье (ДПФ) средствами MATLAB.

• Оценка с помощью прямого и обратного ДПФ полосы частот, в которой сосредоточена основная доля энергии сигнала.

• Наблюдение изменений результатов вычисления ДПФ, происходящих при дополнении сигнала нулевыми отсчетами.

• Оценка степени ускорения вычислений за счет алгоритмов быстрого преобразования Фурье (БПФ).

1. Подготовка к началу работы

Таблица 1 - Параметры сигнала

Вариант	U1, В	U2, В	U3, В	U4, В	Т1, мс	T2, мс	Fд, кГц
20	9	-3	-8	5	3	6	5

Рис.1 – Параметры сигнала

Рис.2 – Формирование дискретного сигнала

Рис.3 – Вид исходного дискретного сигнала

2. Расчёт дискретного преобразования Фурье

Рис.4 – Расчёт ДПФ

Применяется функция fft для вычисления дискретного преобразования Фурье. В итоге функция возвращает массив спектральных коэффициентов длиной N, где каждый элемент соответствует частоте спектрального отсчета n в диапазоне от 0 до N−1. Это включает нулевую частоту (n=0) и последовательно все N−1отсчетов. Полученные спектры отображается на графиках.

Рис.5 – Графики модуля и фазы спектральных отсчётов

3. Оценка ширины спектра сигнала

Рис.6 – Оценка ширины спектра сигнала

С помощью цикла while находится N_max при котором энергия восстановленного сигнала будет больше пороговой энергии E_th равной 90% от энергии исходного сигнала Е0.

Рис.7 – Графики модуля и фазы спектральных отсчётов

Рис.8 – Дискретное представление исходного сигнала вместе с копией

Энергии

Энергия исходного сигнала составляет 588.9 В²

Энергия восстановленного сигнала составляет 558.7 В²

Соотношение

Значит, что около 95% энергии исходного сигнала при ДПФ сосредоточено в 0 и 1 спектральном отсчете (гармонике), то есть N_max = 1.

Тогда ширина спектра в кГц будет равна

4. Дополнение сигнала нулями

Рис.9 – Дополнение сигнала нулями

Создается копия исходного сигнала хk1, затем копия дополняется нулями, количество отсчетов при этом возрастает в 2 раза – вектор n подстраивается под длину исходного сигнала. Затем по аналогии с пунктом 2 строятся амплитудные и фазовые спектры полученных путем ДПФ спектральных отсчетов.

Рис.10 - Графики модуля и фазы спектральных отсчётов сигнала, дополненного нулями

5. Измерение скорости расчётов при вычислении дпф по теоретической формуле

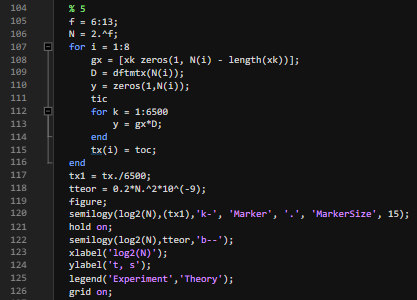
Рис.10 – Измерение скорости расчётов при прямом вычислении ДПФ

Значения N задаются как степени 2, затем с помощью цикла for для каждого размера ДПФ проводятся вычисления с таймером, на выходе значения времени собираются в массив tx, а времени для однократного вычисления в массив tx1. Максимально близкая к расчетам аппроксимирующая прямая задается коэффициентом k₁ = 0.2 * 10^-9 с.

Количество повторений k задается равным 6500, так как при этом значении время вычисления ДПФ размера N = 1024 составляет около 1 с.

Рис.11 – График экспериментальной и теоретической зависимостей для прямого ДПФ

Таблица 2 – Экспериментальные значения времени ДПФ для k = 6500

Параметр	N
	64	128	256	512	1024	2048	4096	8192
Время, с	0.0151	0.0341	0.0622	0.1767	1.0618	6.0926	30.1199	111.5437
Время однократного вычисления ДПФ, мкс	2.3232	5.2463	9.5691	27.1846	163.353	937.323	4633.83	17160.56