Лаба2 / Лаба №2

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ТОР

отчет

по лабораторной работе №2

по дисциплине «Цифровая обработка сигналов»

Тема: Дискретные фильтры

Студенты гр.
Преподаватель		Апалина П.В.

Санкт-Петербург

2024

Цели работы:

1. Пропускание дискретного сигнала через дискретный фильтр и получение графика выходного сигнала;

2. Анализ сигналов, проходящих через элементы памяти фильтра, при реализации фильтра в разных формах;

3. Получение графиков характеристик фильтра с помощью среды визуализации фильтров FVTool;

4. Разложение функции передачи фильтра на простые дроби и получение аналитической формулы для импульсной характеристики фильтра.

Таблица 1 – Исходные данные

Вариант	b0	b1	b2	b3	b4	a0	a1	a2	a3	a4
20	0.0097	-0.0321	0.0454	-0.0321	0.0097	1	-3.5729	4.8079	-2.8863	0.6520

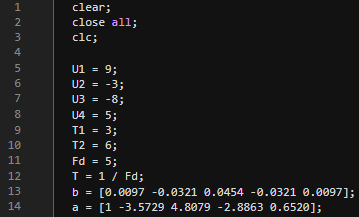
Рис.1 - Параметры сигнала и фильтров

Переменные U1, U2, U3, U4, T1, T2 и Fd задают параметры сигнала: амплитуды и временные интервалы. Массивы b и a содержат коэффициенты фильтра.

Обработка результатов

1. Подготовка к началу работы

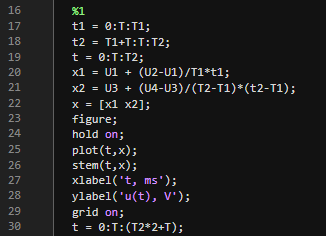
Рис.2 - Создание исходного сигнала

Создаются временные векторы t1 и t2 для каждого отрезка сигнала, и на этих интервалах рассчитываются значения сигнала (x1 и x2) исходя из уравнения прямой заданной начальной и конечной точками.

Эти куски соединяются в единый сигнал x, который отображается массивом t на графике с функциями plot (для линии) и stem (для дискретных точек).

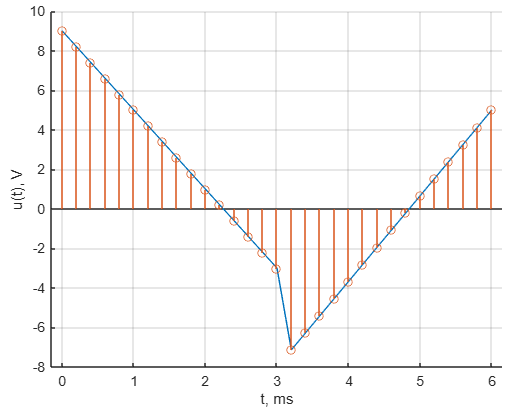
Рис.3 - Исходный сигнал

2. Анализ прямой формы реализации дискретного фильтра

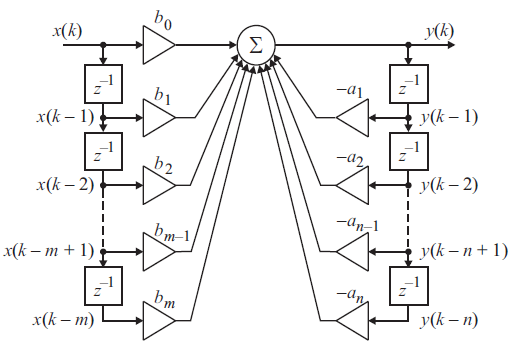
Рис.4 - Структурная схема прямой формы реализации дискретного фильтра

При использовании прямой формы реализации дискретного фильтра в элементах памяти (элементах задержки) хранятся непосредственно отсчеты входного и выходного сигналов

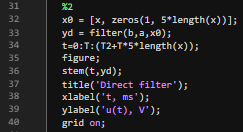
Рис.5 - Реализация прямого дискретного фильтра

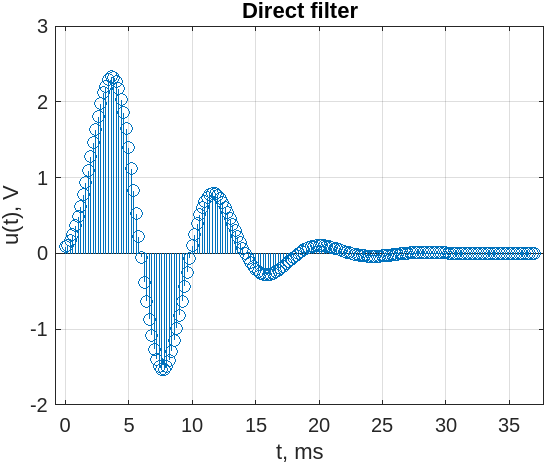
Рис.6 - Выходной сигнал прямого дискретного фильтра

3. Анализ канонической формы реализации дискретного фильтра

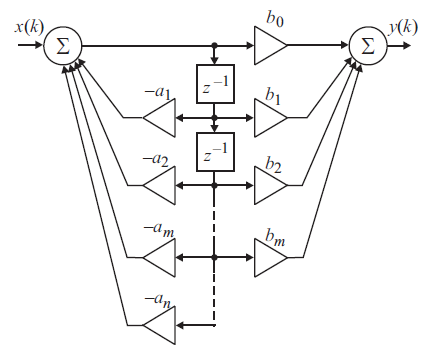
Рис.7 - Структурная схема канонической формы реализации дискретного фильтра

При использовании канонической формы реализации дискретного фильтра в элементах памяти хранятся отсчеты сигнала, прошедшего через рекурсивную часть фильтра

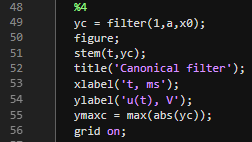
Рис.8 – Реализация канонического дискретного фильтра

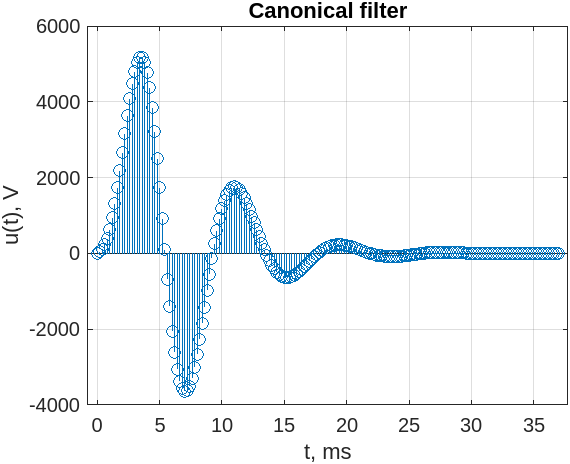
Рис.9 - Сигнал, хранящийся в элементах памяти фильтра, реализованного в соответствии с канонической формой

4. Анализ транспонированной формы реализации дискретного фильтра

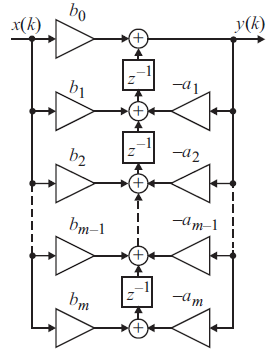
Рис.10 - Структурная схема транспонированной формы реализации дискретного фильтра

Элементы памяти не образуют линию задержки, поэтому в данном случае необходимо получить графики для всех сигналов, проходящих через элементы памяти фильтра.

Рис.11 - Функция дискретного фильтра

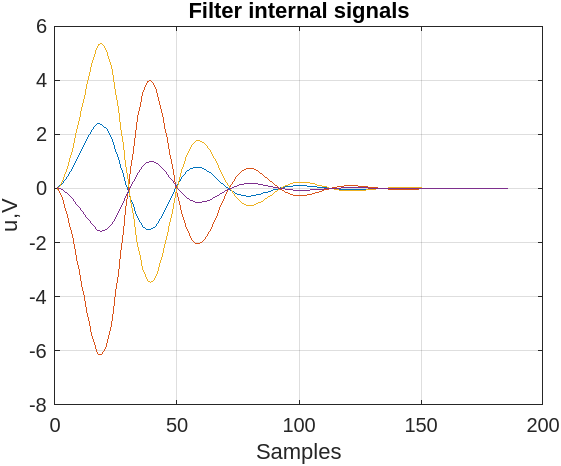
Рис.12 - Внутренние сигналы дискретного фильтра

5. Сравнение максимальных по модулю значений сигнала разных форм реализации фильтров

Таблица 2 – Найденные максимальные значения сигналов

Форма реализации фильтра	Максимальное по модулю внутреннее состояние
Прямая	9
Каноническая	5171.5
Транспонированная	6.1398

6. Получение графиков характеристик фильтра

Рис.13 - Вызов среды FVTool

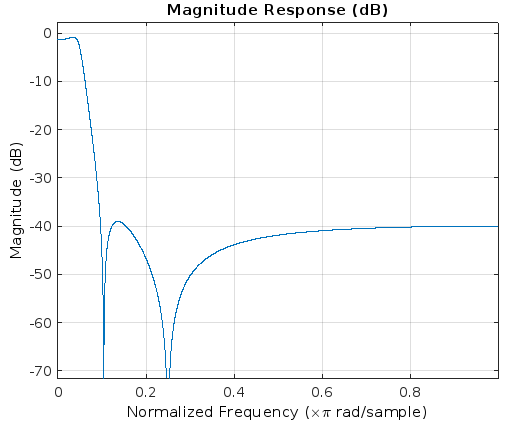
Рис.14 - АЧХ фильтра

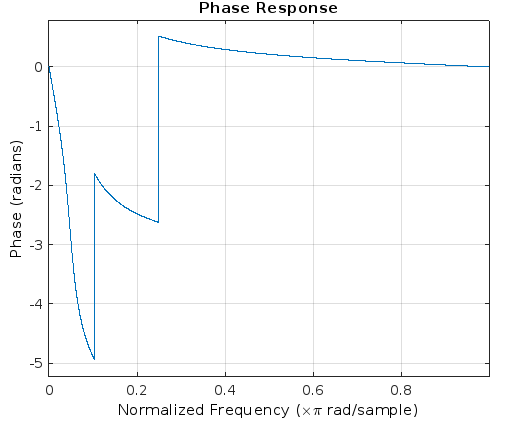
Рис.15 - ФЧХ фильтра

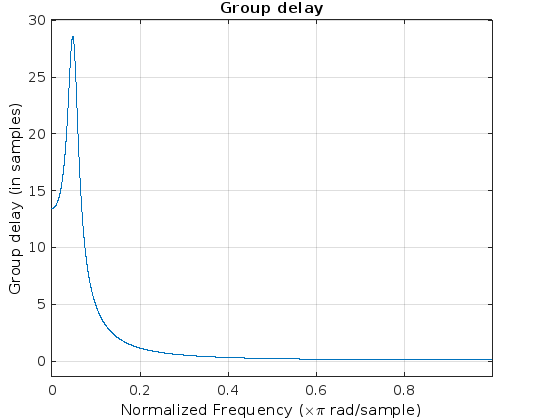
Рис.16 - Групповая задержка

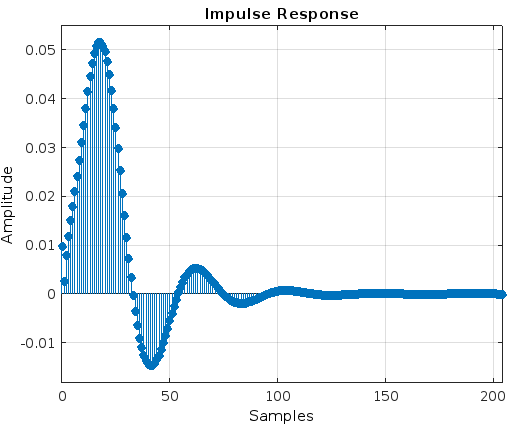
Рис.17 - Импульсная характеристика

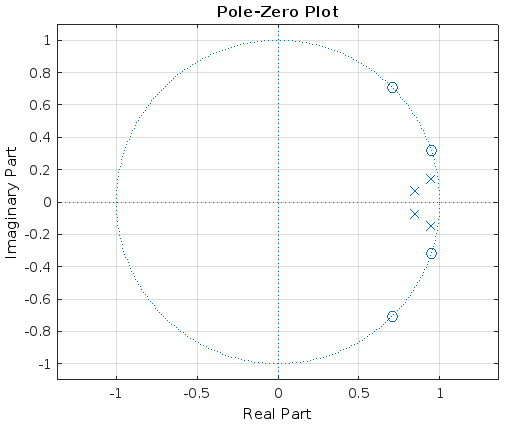
Рис.18 - Расположение нулей и полюсов функции передачи на комплексной плоскости

7. Получение аналитической формулы для импульсной характеристики фильтра

Рис.19 - Получение вычетов, полюсов и целой части

Таблица 3 - Модули и фазы полюсов и вычетов

	Модуль	Фаза, рад
	Вычеты
r1	0.0554	2.904
r2	0.0554	-2.904
r3	0.1557	-1.2351
r4	0.1557	1.2351
	Полюса
p1	0.9531	0.1504
p2	0.9531	-0.1504
p3	0.8472	0.0853
p4	0.8472	-0.0853
	Целая часть
k	0.0149

На основе найденных данных составляется аналитическая формула для импульсной характеристики фильтра в комплексной форме с помощью дробно-рационального вида функции передачи

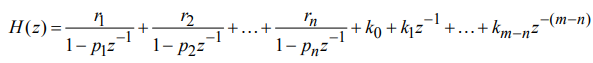
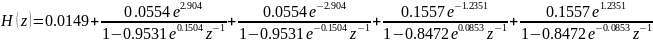
Приведение импульсной характеристики к вещественному виду путем суммирования комплексно-сопряженных пар

Суммирование 1 пары

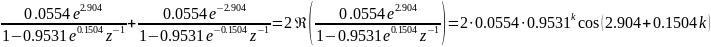
Суммирование 2 пары

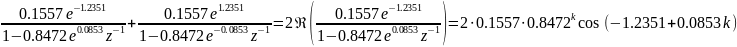
Итоговая вещественная импульсная характеристика

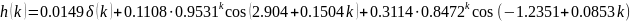
Вывод

в ходе данной лабораторной работы изучены и реализованы методы анализа дискретных фильтров с акцентом на их основные характеристики и внутренние состояния. Были исследованы фильтры в различных представлениях (прямой, канонический, транспонированный) и построены соответствующие графики. Также произведен анализ устойчивости фильтра через его полюса и нули. Графическое представление импульсной характеристики позволило визуализировать отклик системы, что подтвердило её свойства, такие как затухающие колебания и характерные частотные составляющие. В результате была получена полная картина поведения и характеристик дискретных систем, что подтверждает их свойства на практике.

Листинг кода

clear;

close all;

clc;

% Задание параметров для сигналов и фильтра

U1 = 9;

U2 = -3;

U3 = -8;

U4 = 5;

T1 = 3;

T2 = 6;

Fd = 5;

T = 1 / Fd;

b = [0.0097 -0.0321 0.0454 -0.0321 0.0097];

a = [1 -3.5729 4.8079 -2.8863 0.6520];

% 1. Построение исходного сигнала

t1 = 0:T:T1;

t2 = T1+T:T:T2;

t = 0:T:T2;

x1 = U1 + (U2-U1)/T1*t1;

x2 = U3 + (U4-U3)/(T2-T1)*(t2-T1);

x = [x1 x2];

% График исходного сигнала

figure;

hold on;

plot(t,x);

stem(t,x);

xlabel('t, ms');

ylabel('u(t), V');

grid on;

% 2. Применение фильтра

t = 0:T:(T2+2*5* length(x)); % Обновление временной оси

x0 = [x, zeros(1, 5*length(x))]; % Дополнение сигнала нулями

yd = filter(b, a, x0); % Применение прямого фильтра

figure;

stem(t, yd); % График отфильтрованного сигнала

title('Direct filter');

xlabel('t, ms');

ylabel('u(t), V');

grid on;

% 3. Нахождение максимальных значений сигнала

ymaxd = max(abs(yd)); % Максимум амплитуды фильтрованного сигнала

xmax = max(abs(x0)); % Максимум амплитуды исходного сигнала

maxd = max(xmax, ymaxd); % Максимум из этих значений

% 4. Каноническая форма фильтра

yc = filter(1, a, x0); % Применение канонической формы фильтра

figure;

stem(t, yc); % График сигнала после фильтрации

title('Canonical filter');

xlabel('t, ms');

ylabel('u(t), V');

ymaxc = max(abs(yc)); % Максимум канонического сигнала

grid on;

% 5. Анализ состояний фильтра

states = []; % Инициализация массива состояний

s = []; % Инициализация переменной для состояний фильтра

for i = 1:length(x0) % Цикл по каждому отсчету сигнала

[yt(i), s] = filter(b, a, x0(i), s);

states = [states s]; % Добавление состояний в массив

end

% График состояний фильтра

figure;

plot(states');

ymaxt = max(max(abs(states'))); % Нахождение максимума состояний

grid on;

title('Filter internal signals');

xlabel('Samples');

ylabel('u,V');

% 6. Анализ фильтра с помощью fvtool

fvtool(b, a, 'magnitude'); % График амплитудной характеристики

fvtool(b, a, 'phase'); % График фазовой характеристики

fvtool(b, a, 'grpdelay'); % График задержки группы фильтра

fvtool(b, a, 'impulse'); % График импульсной характеристики

fvtool(b, a, 'polezero'); % График полюсов и нулей фильтра

% 7. Разложение фильтра на вычеты, полюса и коэффициенты

[r, p, k] = residuez(b, a); % Разложение на вычеты, полюса и коэффициенты

rab = abs(r); % Модуль вычетов

ran = angle(r); % Фаза вычетов

pab = abs(p); % Модуль полюсов

pan = angle(p); % Фаза полюсов

k; % Коэффициент k фильтра