Лаба1 / Лаба №1

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ТОР

отчет

по лабораторной работе №1

по дисциплине «Цифровая обработка сигналов»

Тема: Дискретные сигналы

Студенты гр. 3		.
Преподаватель		Апалина П.В.

Санкт-Петербург

2024

Цели работы:

• Знакомство со средой MatLab;

• Формирование и построение графика кусочно-линейного дискретного сигнала;

• Расчёт и построение графика спектра дискретного сигнала;

• Расчёт и построение графика аналогового сигнала, восстановленного по дискретным отсчётам в соответствии с теоремой Котельникова.

Индивидуальное задание

В данной лабораторной работе рассматривается кусочно-линейный сигнал s(t), заданный параметрами U_k, T_k, k = 1…4. При выполнении работы производится дискретизация данного сигнала с заданной частотой F_д.

Таблица 1 - Параметры сигнала

Вариант	U1, В	U2, В	U3, В	U4, В	Т1, мс	T2, мс	Fд, кГц
20	9	-3	-8	5	3	6	5

Рис.1 – Параметры сигнала

Устанавливаются начальные параметры уровня сигнала (U1, U2, U3, U4), моменты времени (T1, T2), частота дискретизации Fd, и шаг дискретизации T.

1. Формирование дискретного сигнала

Рис.2 - Код задания №1

Создаются временные векторы t1 и t2 для каждого отрезка сигнала, и на этих интервалах рассчитываются значения сигнала (u1 и u2) исходя из уравнения прямой заданной начальной и конечной точками.

Эти куски соединяются в единый сигнал u, который отображается на графике с функциями plot (для линии) и stem (для дискретных точек).

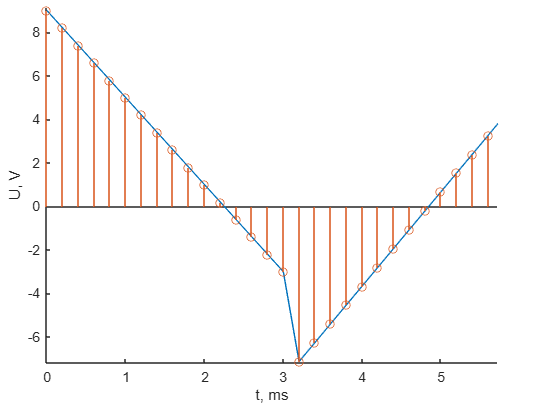
Рис.2 - Дискретный сигнал

2. Построение графика спектра дискретного сигнала

Спектр дискретного сигнала рассчитывается по формуле:

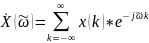
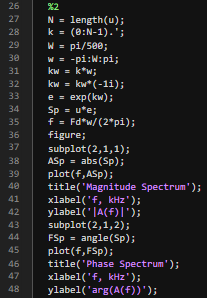
Рис.3 - Код задания №2

Определяется длина сигнала N, вектор индексов k, и вектор частот w.

Формула преобразования Фурье реализуется через матричное умножение сигнала u на комплексные экспоненты (exp(kw)). Это дает спектр сигнала Sp.

Спектр визуализируется в двух графиках: амплитудный спектр |A(f)| и фазовый спектр arg(A(f)).

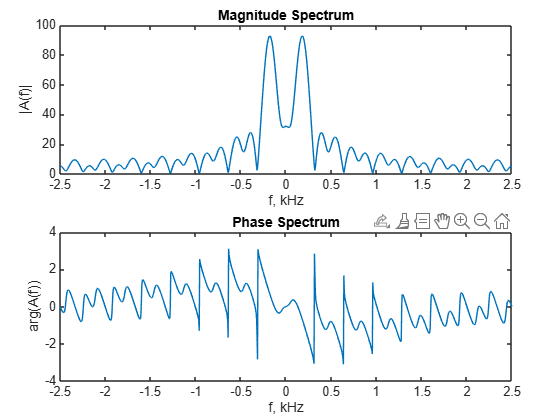
Рис.4 - Амплитудный и фазовый спектры сигнала

3. Восстановление аналогового сигнала по теореме Котельникова

Восстановление аналогового сигнала s(t) с ограниченным спектром по его дискретным отсчетам x(k) в соответствии с теоремой Котельникова производится по формуле:

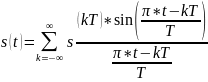
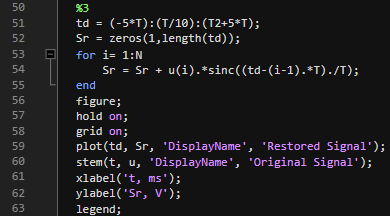
Рис.5 - Код задания №3

Определяется временной вектор td с более высокой разрешающей способностью для восстановления аналогового сигнала.

Используя функцию sinc, рассчитывается восстановленный аналоговый сигнал Sr путем суммирования sinc-функций для каждого отсчета.

Построение графика восстановленного сигнала вместе с исходным дискретным сигналом позволяет наглядно увидеть качество восстановления.

Рис.6 - Исходный дискретный и восстановленный аналоговый сигналы

Вывод

В ходе выполнения лабораторной работы был сформирован кусочно-линейный дискретный сигнал, рассчитан его спектр и восстановлен аналоговый сигнал; дискретный и восстановленный сигналы весьма близки, что подтверждает теорему Котельникова. Это свидетельствует о том, что при частоте дискретизации, достаточной для выполнения условий теоремы, исходный аналоговый сигнал может быть достаточно точно восстановлен из дискретных отсчетов.

Проведённый анализ спектра показал периодичность и наличие основных частотных компонентов, характерных для дискретного сигнала, а восстановленный сигнал наглядно демонстрирует точность и эффективность метода, базирующегося на sinc-интерполяции.

Листинг кода

close all;

% Определение параметров сигналов

U1 = 9;

U2 = -3;

U3 = -8;

U4 = 5;

T1 = 3;

T2 = 6;

Fd = 5;

T = 1 / Fd;

% 1. Построение исходного сигнала

t1 = 0:T:T1; % Вектор времени для первого сигнала

t2 = T1+T:T:T2; % Вектор времени для второго сигнала

t = 0:T:T2; % Общее время

u1 = U1 + (U2-U1)/T1*t1; % Линейное изменение сигнала 1

u2 = U3 + (U4-U3)/(T2-T1)*(t2-T1); % Линейное изменение сигнала 2

u = [u1 u2]; % Объединение двух сигналов

% График исходного сигнала

figure;

hold on;

plot(t,u); % Линия для сигнала

stem(t,u); % Столбцы для дискретных отсчетов

xlabel('t, ms');

ylabel('U, V');

% 2. Спектральный анализ сигнала с использованием ПФ

N = length(u); % Длина сигнала

k = (0:N-1).'; % Вектор индексов для ПФ

W = pi/500; % Разрешение частоты

w = -pi:W:pi; % Частотная ось

kw = k * w; % Матрица частот

kw = kw * (-1i); % Умножение на мнимую единицу

e = exp(kw); % Вычисление экспоненты для спектра

Sp = u * e; % Расчет спектра сигнала

f = Fd * w / (2*pi); % Частотная ось в кГц

% Графики амплитудного и фазового спектра

figure;

subplot(2,1,1);

ASp = abs(Sp); % Модуль спектра

plot(f, ASp); % График амплитудного спектра

title('Magnitude Spectrum');

xlabel('f, kHz');

ylabel('|A(f)|');

subplot(2,1,2);

FSp = angle(Sp); % Фаза спектра

plot(f, FSp); % График фазового спектра

title('Phase Spectrum');

xlabel('f, kHz');

ylabel('arg(A(f))');

% 3. Восстановление сигнала через интерполяцию

td = (-5*T):(T/10):(T2+5*T); % Новый временной вектор

Sr = zeros(1,length(td)); % Инициализация восстановленного сигнала

% Интерполяция с помощью sinc-функции

for i = 1:N

Sr = Sr + u(i) .* sinc((td - (i-1)*T) / T);

end

% График восстановленного сигнала

figure;

hold on;

grid on;

plot(td, Sr, 'DisplayName', 'Restored Signal'); % Восстановленный

stem(t, u, 'DisplayName', 'Original Signal'); % Исходный сигнал

xlabel('t, ms');

ylabel('Sr, V');

legend;