Обработка результатов:

Вследствие неисправности установки, опыт будет описан словами, и все зависимости будут показаны аналитически.

При распылении масло превращается в мелкодисперсную струю, и мы можем видеть в окуляр множество маленьких капель, парящих в воздухе (рис. 2). Это явление внешне можно сравнить со звёздным небом.

Рис. 2 – Фотография изображения в окуляре микрометра

При нормальных условиях капли будут медленно падать под действием силы тяжести. Если мы зарядим пластины конденсатора, между ними возникнет электрическое поле. Теперь на капли помимо силы тяжести будет действовать электрическая сила (рис. 3), и скорость её движения будет другой. От размера капли, её заряда и напряжения на обкладках зависит скорость и направление движения. Сопоставляя скорости, Милликен смог математически рассчитать заряды разных капель и вывести элементарный.

Рис. 3 – Силы, действующие на каплю

В лабораторной работе нам предлагается измерить время падения и подъема капель, из чего, зная путь, пройденный ими, в делениях микрометра, вывести скорость. Также нужно рассчитать радиус, заряд и кратность заряда каждой капли. В расчетах необходимо учитывать силу, обусловленную вязкостью (сопротивлением) воздуха – силу трения Стокса.

Найти скорость падения-подъема просто через соответствующее время и путь, которые мы измеряем в ходе экперимента: .

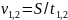Радиус 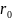легко находится из равновесия сил между результирующей гравитационной силой 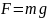и силой трения Стокса 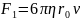. Массу капли распишем через объем и плотность, при этом важно учесть разность плотностей масла и воздуха. Тогда 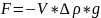. Объем капли также распишем как .

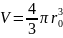Из равенства 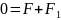получим:

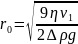
Теперь, зная скорости и радиус, можем рассчитать заряд. После включения напряжения добавилась сила qE, действующая на каплю зарядом q со стороны электрического поля E. Следуют измерения установившейся скорости 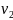 . Капля движется равномерно, следовательно, силы уравновешены:

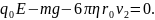
Учитывая, что :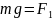

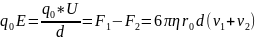
Таким образом:

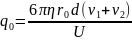
Кратность заряда ищем из закона дискретности. Каждая капля, в зависимости от размера, будет иметь разную скорость, соответственно и величина заряда будет отличаться. Но она всегда будет кратна элементарному заряду электрона: 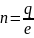. Т.е. в теории мы могли бы рассчитать, как и Милликен, заряды 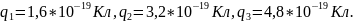Что соответственно равно

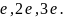
Вывод: Чтобы найти заряд капли, нужно знать скорость падения-подъема и радиус капли. Скорость находим из расстояния и времени. Радиус находим из связи силы тяжести и силы трения. В итоге можно найти заряд из результирующей сил электрической, тяжести и трения. Кратность считаем из закона дискретности заряда.