лаб3.3_рэ
.docМИНОБРНАУКИ РОССИИ
«Челябинский государственный университет»
(ФГБОУ ВПО «ЧелГУ»)
Физический факультет
Кафедра радиофизики и электроники
ОТЧЕТ
ЛАБОРАТОРНАЯ РАБОТА №3_3
ТЕМА: Линейные цепи. Резонансные RLC цепи.
ВЫПОЛНИЛ СТУДЕНТ |
|||
|
|||
Агеев А.А. |
|||
|
|||
Академическая группа |
ФФ-204 |
Курс |
2 |
|
|||
(подпись)
« » 2024г. |
|||
|
|||
ПРОВЕРИЛ |
|||
|
|||
Зотов И.С. |
|||
|
|||
|
|||
ОЦЕНКА: |
|||
|
|||
|
|||
(подпись)
« » 2024г. |
|||
Челябинск
2024
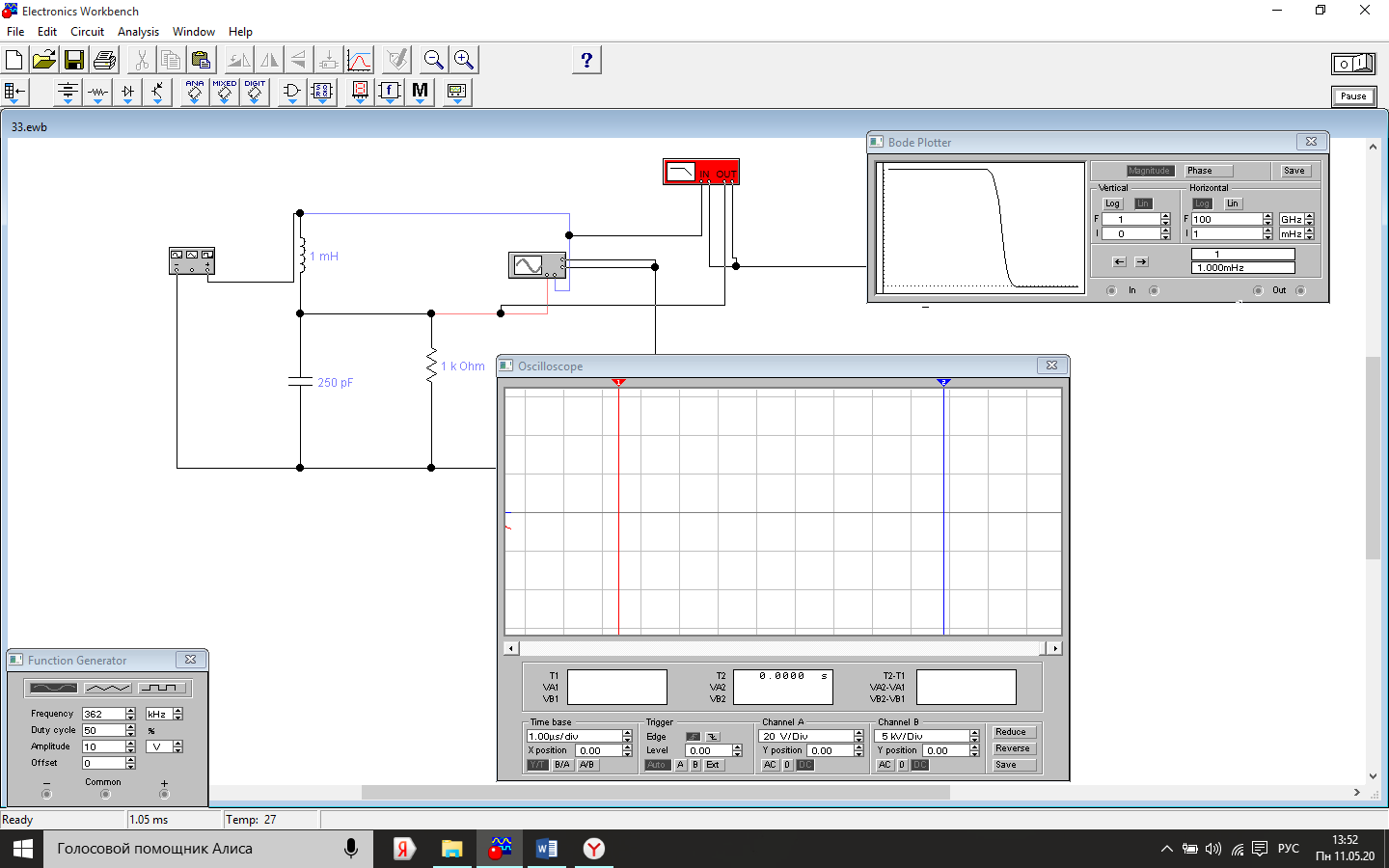
3. Последовательный колебательный контур. LC-фильтр низких частот.

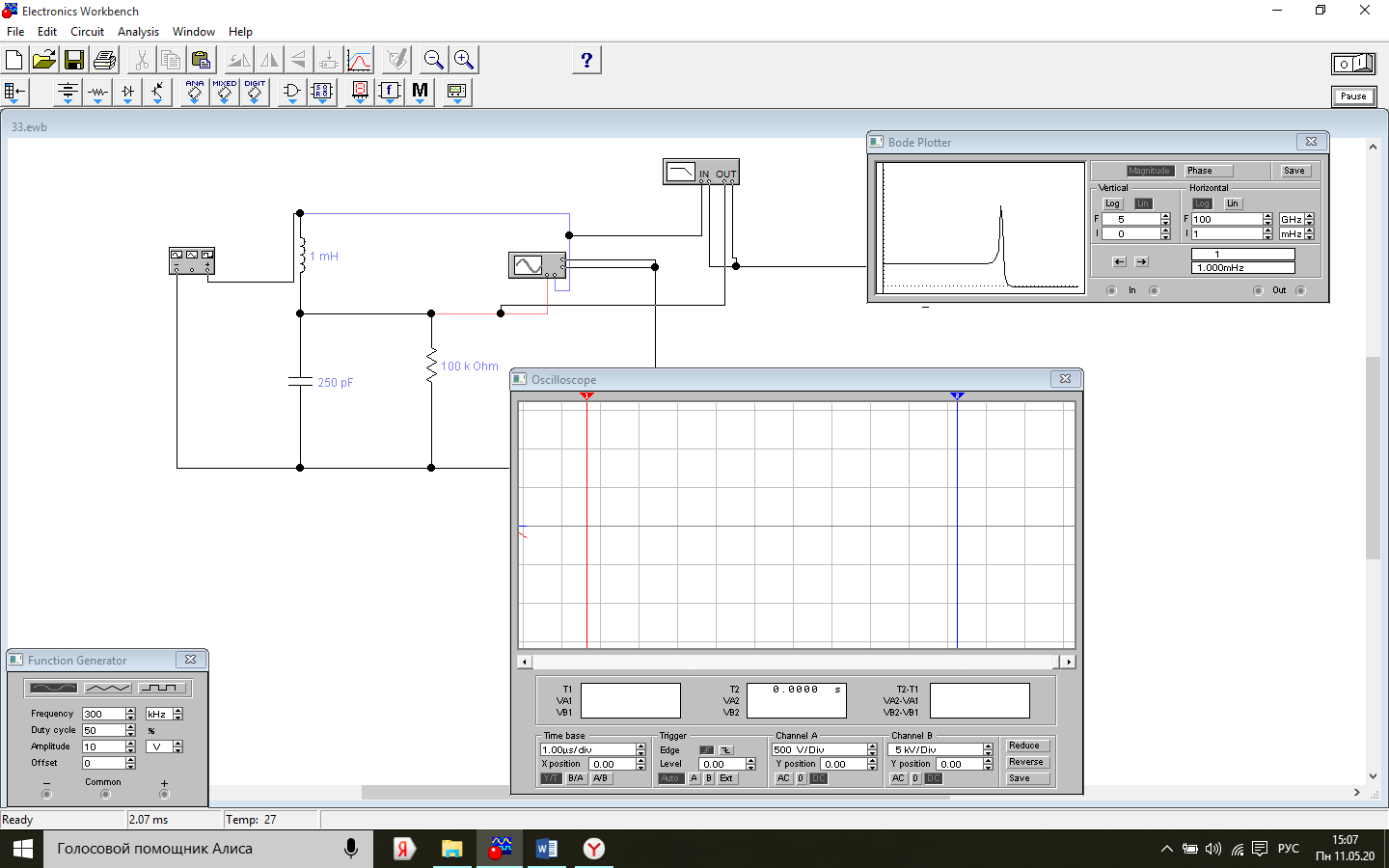
Схема установки.
Величина амплитуды входного напряжения Uin=10В, катушки индуктивности L=1 mH, резистора R=20КОм номинал конденсатора C =250pF
Измерения амплитудно-частотной характеристики.
f,КГц |
Uout, В |
K=Uout/Uin |
1 |
10 |
1 |
50 |
10.2 |
1,02 |
100 |
11 |
1,1 |
150 |
12.8 |
1,28 |
250 |
26.6 |
2,66 |
300 |
75.4 |
7,54 |
310 |
97.5 |
9,75 |
313.1 |
100 |
10 |
315 |
97.5 |
9,75 |
320 |
91.5 |
9,15 |
350 |
37 |
3,7 |
450 |
9.45 |
0,945 |
600 |
3.75 |
0,375 |
1000 |
1 |
0,1 |
10000 |
0 |
0 |
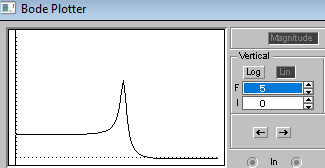
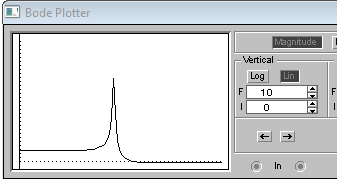
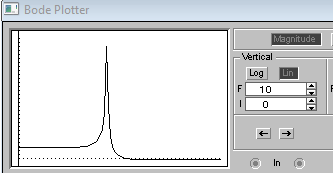
График зависимости K от частоты f.
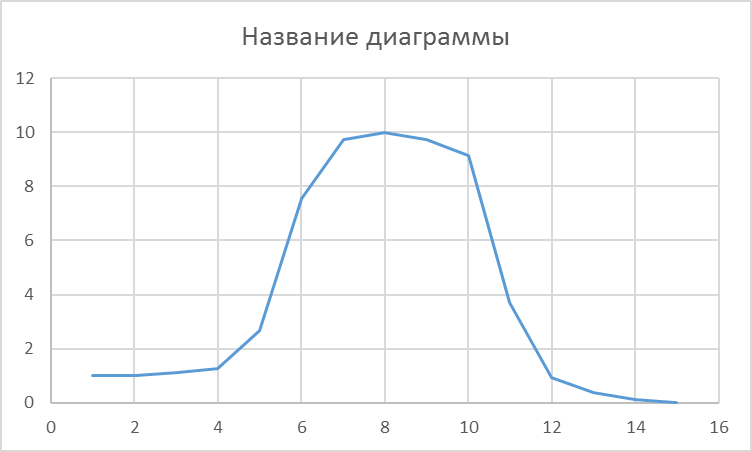
Значения амплитуды выходного сигнала могут значительно превышать (в десятки раз) значения амплитуды входного сигнала в следствии резонанса напряжений при совпадении частоты генератора и контура.
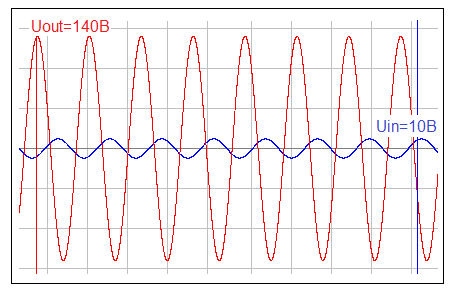
Измерения фазо-частотной характеристики.
f,КГц |
∆t,с |
φ, °град. |
1 |
0 |
0 |
50 |
50нс |
0,9 |
100 |
55нс |
1,98 |
150 |
62.5нс |
3,38 |
250 |
129нс |
11,61 |
300 |
437нс |
47,2 |
310 |
680нс |
75,89 |
313.1 |
764нс |
91,27 |
315 |
818нс |
92,76 |
320 |
951нс |
109,56 |
350 |
1.6мкс |
201,6 |
450 |
1.16мкс |
189,54 |
600 |
848нс |
183,17 |
1000 |
480нс |
172,8 |
10000 |
50нс |
180 |
График
зависимости φ
от частоты f.
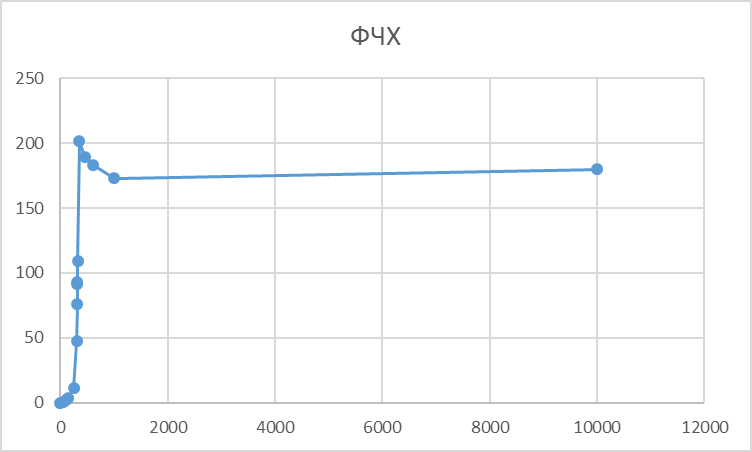
Теоретическое значение резонансной частоты последовательного колебательного контура fо=1/(2π√LС)=318.3 кГц По графику АЧХ определим: fоэкс=313.1кГц, fср=487.5кГц LC-фильтра нижних частот, ∆f=31.6кГц
Рассчитаем: теоретическое значение добротности последовательного колебательного контура Q=R*√(C/L)=10 Qэкс=fоэкс/∆f=9.91
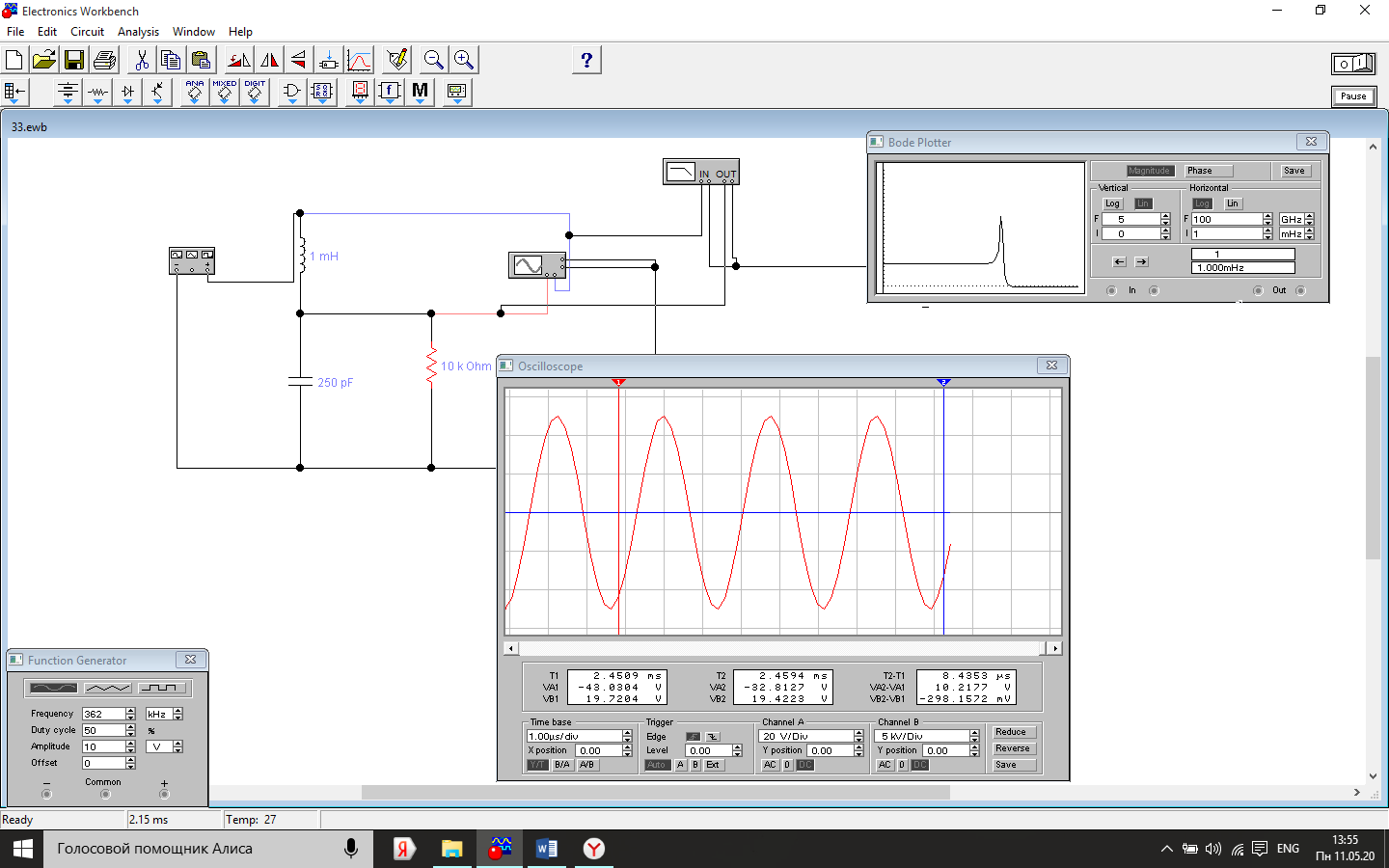
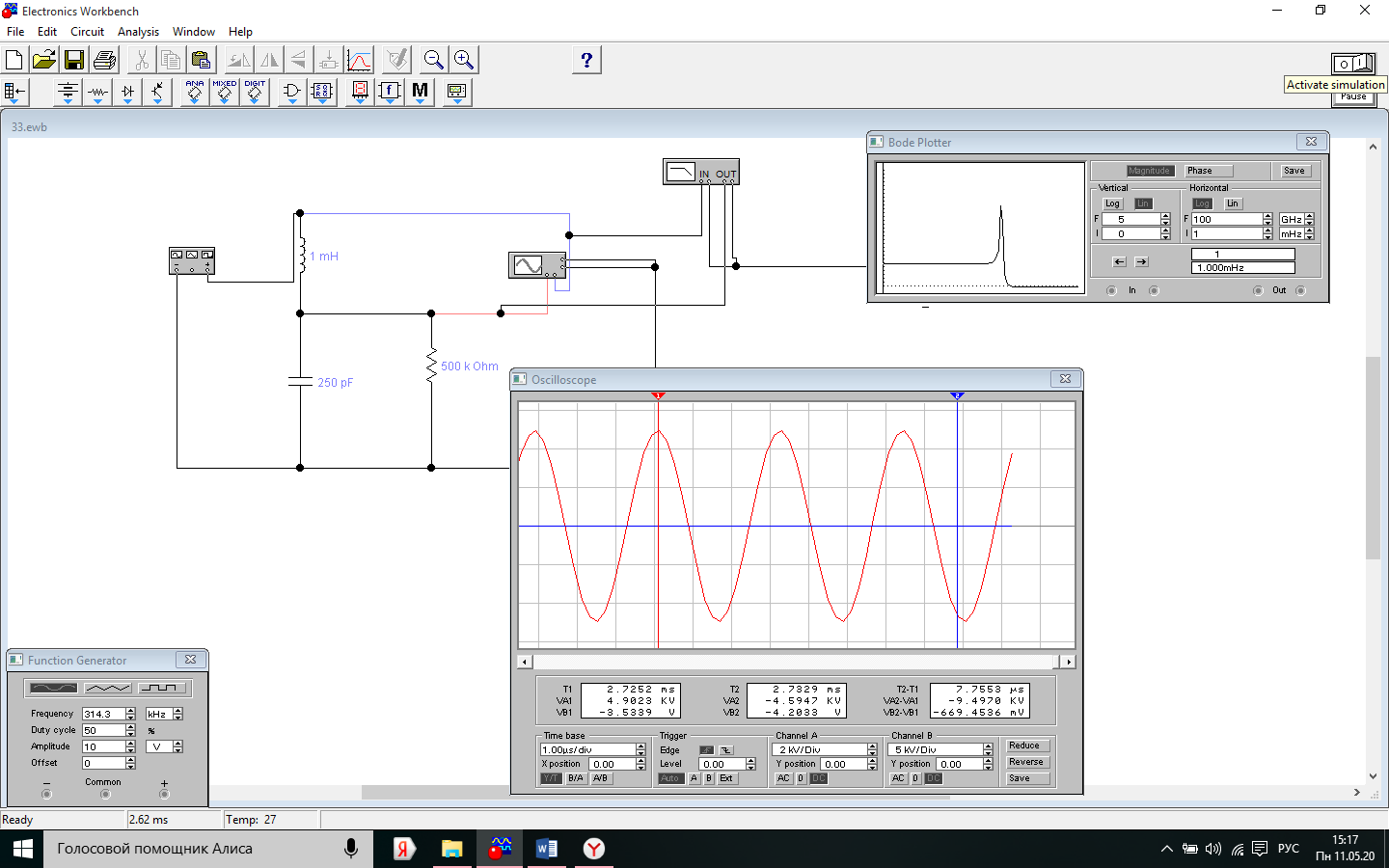
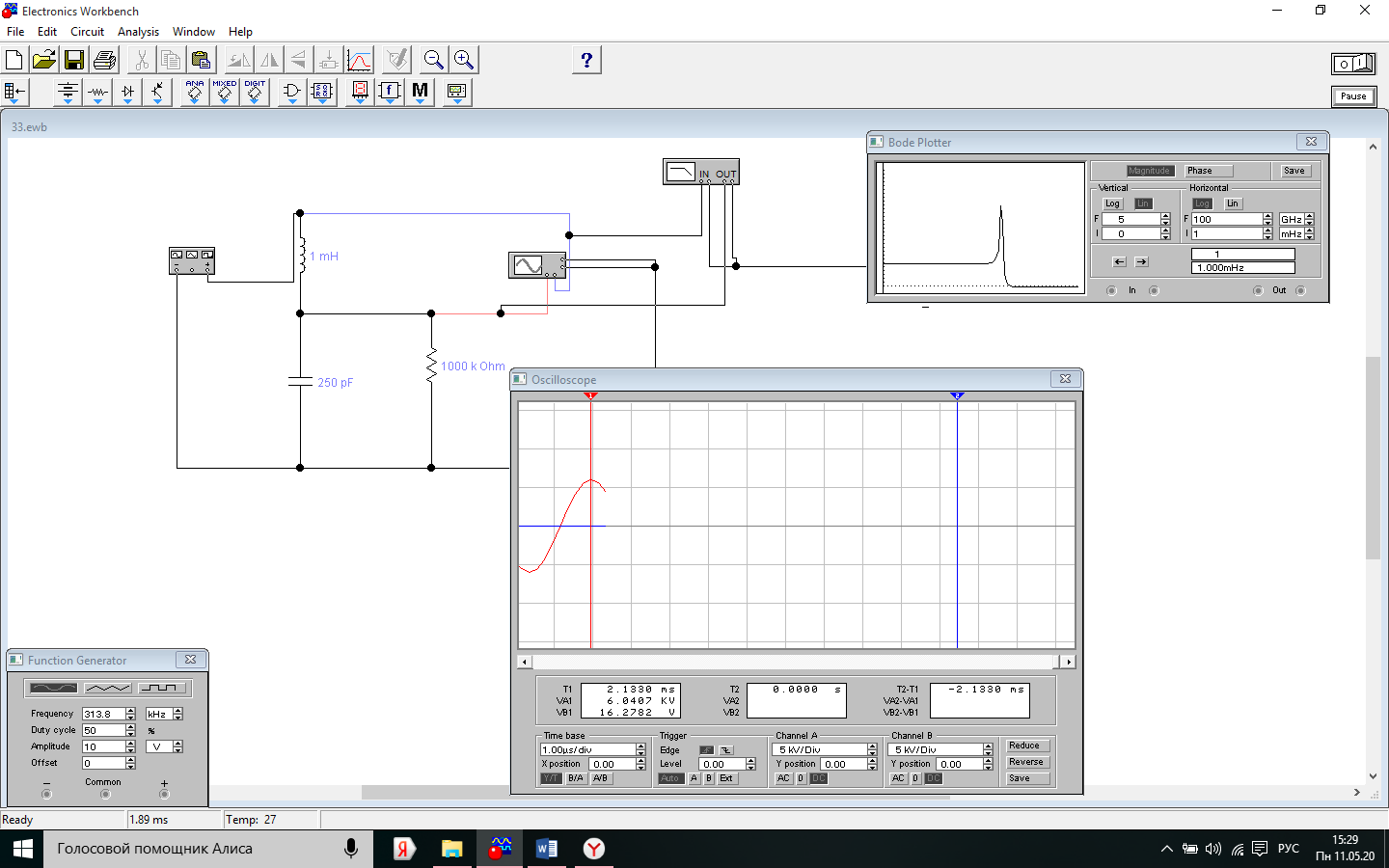
Осциллограмма
переходного процесса характерного для
резонансной колебательной системы при
значении нагрузочного резистора
R=100КОм.
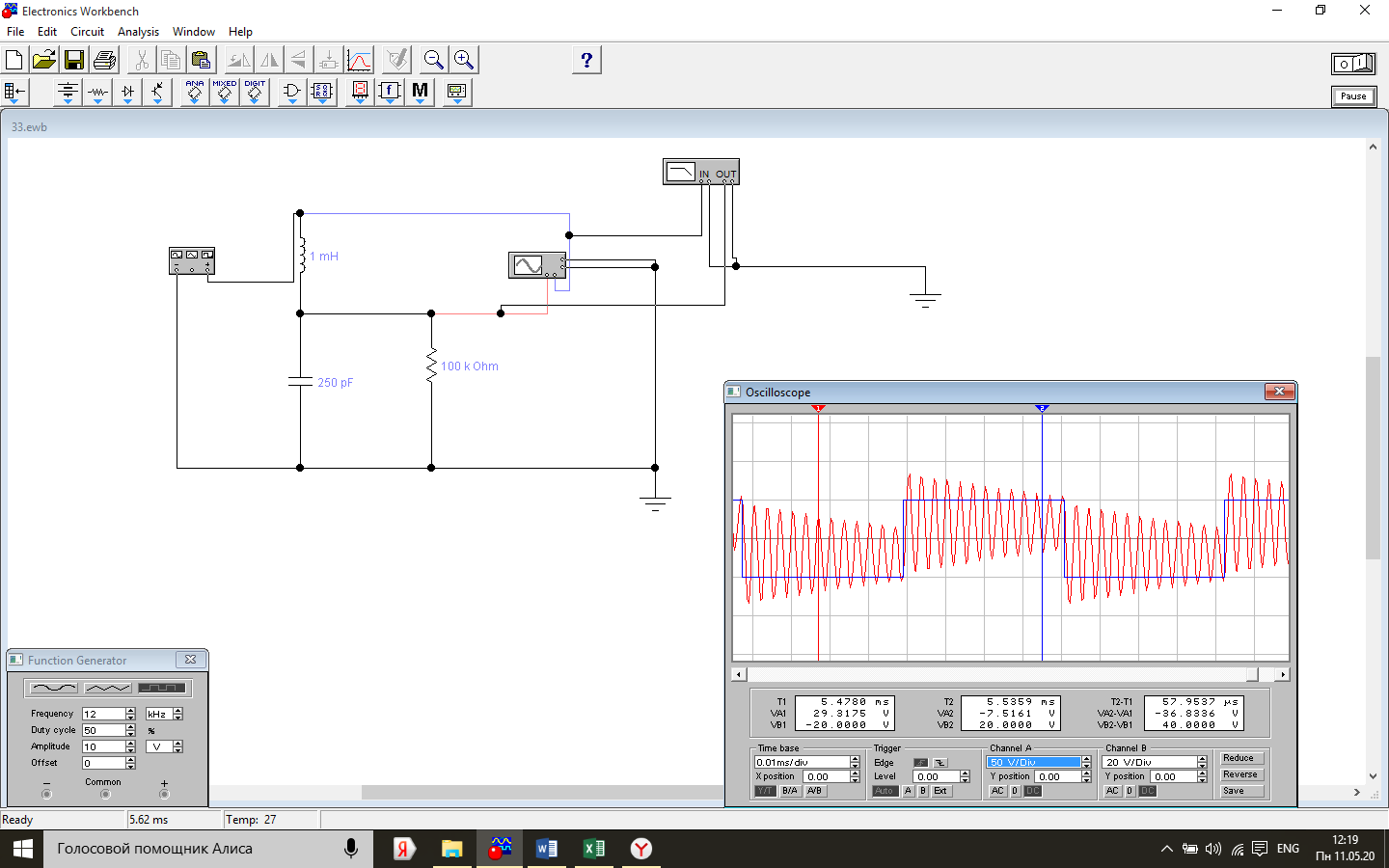
По графику переходного процесса экспериментально измерим: fс=1/T=303кГц
α=R/2L= 50000000 U(t)=83.8969 и U(t+T)= 78.6344 Рассчитаем: Qэкс=15.94 теоретическое значение добротности Q=50
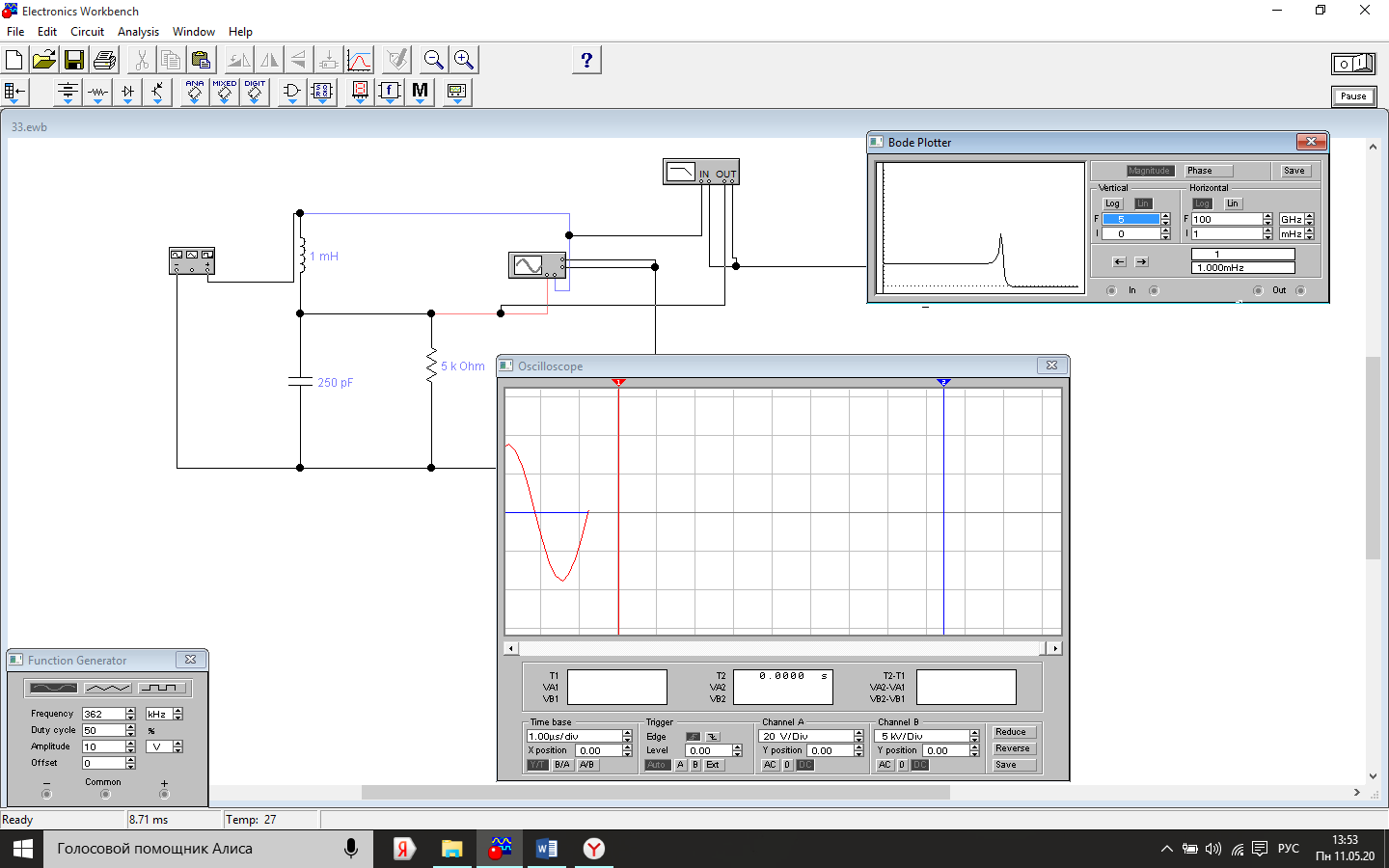
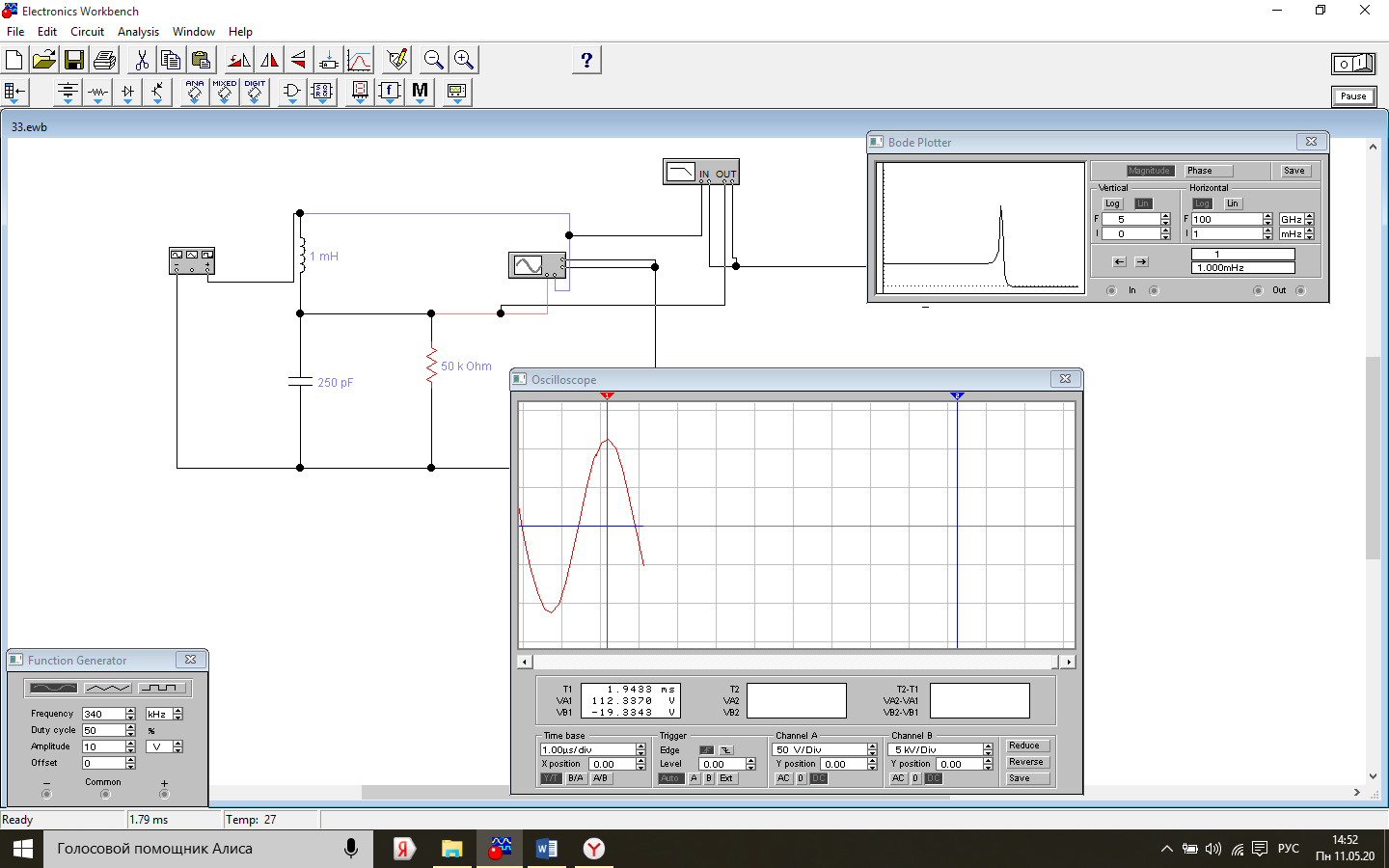
Зависимость добротности колебательного контура Q от значения сопротивления R
R, КОм |
fр, КГц |
∆f, КГц |
Qэкс |
Qт |
|
1 |
313 |
? |
? |
0.5 |
|
5 |
310 |
137 |
2.26 |
2.5 |
|
10 |
311 |
66 |
4.71 |
5 |
|
50 |
314.6 |
9.8 |
32.1 |
25 |
|
100 |
313.9 |
6.3 |
49.8 |
50 |
|
500 |
314.2 |
1.4 |
224.4 |
250 |
|
1000 |
314.2 |
0.6 |
523.7 |
500 |
|
Зависимость добротности колебательного контура Q от значения емкости конденсатора С, при значении резистора R=10КОм.
С, nF |
fр, КГц |
∆f, КГц |
Qэкс |
Qт |
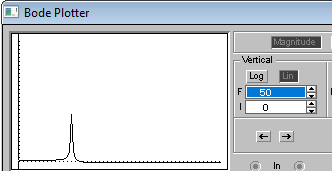
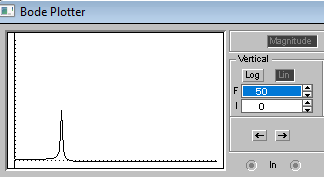
АЧХ |
0.1 |
498.1 |
174 |
2.86 |
3.16 |
|
0.5 |
222.9 |
31.9 |
7 |
7.07 |
|
1 |
157 |
15.6 |
10.01 |
10 |
|
50 |
22.2 |
0.3 |
74 |
70.71 |
|
100 |
15.7 |
|
|
100 |
|
500 |
7 |
0.032 |
218.75 |
223.6 |
|
1000 |
5 |
0.016 |
312.5 |
316.23 |
|