
- •Умова мінімумів: результуюче коливання ослаблюється, якщо різниця ходу доданих хвиль дорівнює непарному числу півхвиль:
- •Вимірюючи UЗ, можна визначити максимальну кінетичну енергію фотоелектронів:
- •Цю формулу прийнято називати рівнянням Ейнштейна для фотоефекту.
- •Як випливає із рівняння Ейнштейна, тангенс кута нахилу прямій, що виражає залежність замикаючого потенціалу UЗ від частоти ν, дорівнює відношенню постійної Планка h до заряду електрона e:
- •Це дозволяє експериментально визначити значення постійної Планка. Такі виміри були виконані в 1914 р. Р. Міллікеном і дали гарну згоду зі значенням, знайденим Планком. Ці виміри дозволили також визначити роботу виходу A:
- •Отже, закони фотоефекта свідчать, що світло при випромінюванні й поглинанні поводиться подібно потоку часток, що одержали назву фотонів або світлових квантів.
- •Енергія фотонів дорівнює
- •випливає, що фотон має імпульс
- •Перетворення Лоренца мають вигляд:
- •Тривалість τ процесу в системі K буде дорівнювати:
- •Перший постулат Бора (постулат стаціонарних станів) говорить: атомна система може перебувати тільки в особливих стаціонарних або квантових станах, кожному з яких відповідає певна енергія En. У стаціонарних станах атом не випромінює.
- •де h – стала Планка. Звідси можна виразити частоту випромінювання:
- •Загальне число нуклонів (тобто протонів і нейтронів) називають масовим числом A:
- •Ядра хімічних елементів позначають символом ZAX, де X – хімічний символ елемента. Наприклад,
- •Закон радіоактивного розпаду
- •Енергетичним виходом ядерної реакції називається величина:

1.Механіка. Основні формули.
Назва |
Величина, її визначення |
Основи кінематики Нерівномірний рух vмит - миттєва швидкість;
vсер - середня шляхова швидкість;
t - час;
 - середня швидкість переміщення;
- середня швидкість переміщення;
 - переміщення.
- переміщення.
Рівномірний прямолінійний рух
 - переміщення;
- переміщення;
 - швидкість; t - час
- швидкість; t - час
x - координата;
vx - проекція вектора швидкості на вісь Oх;
Sx - проекція вектора переміщення
Рівнозмінний прямолінійний рух
 - переміщення;
- переміщення;
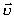 0 - швидкість; t - час;
0 - швидкість; t - час;
 - прискорення;
- прискорення;
Sx - проекція вектора переміщення;
ax - проекція прискорення на вісь Oх;
 0x - проекція вектора швидкості на вісь Oх;
0x - проекція вектора швидкості на вісь Oх;
x - координата;
Одиниця
вимірювання
м/с
м/с
c
м/с
м
м
м/c
с
м
м/с
м
м
м/с
с
м/с2
м
м/с2
м/с
м

Рівномірний рух по колу |
|
R - радіус кола, |
м |
T - період обертання, |
c |
n - частота обертання, |
1/c |
N - кількість обертів |
|
t - час |
c |
w - кутова швидкість, |
рад/с |
j - кут повороту, |
радіан |
aд - доцентрове прискорення |
м/с2 |
Другий закон Ньютона
Третій закон Ньютона
Закон Гука
(Fпр)x = – kx
Закон всесвітнього тяжіння
Основи динаміки
 - сила, що діє на тіло; m - маса тіла;
- сила, що діє на тіло; m - маса тіла;
 - прискорення надане тілу. t - час дії сили;
- прискорення надане тілу. t - час дії сили;
 - швидкість тіла, набута після дії сили F;
- швидкість тіла, набута після дії сили F;
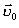 - початкова швидкість тіла.
- початкова швидкість тіла.
 ;
;  - сили, що діють на тіла під час взаємодії.
- сили, що діють на тіла під час взаємодії.
(Fпр)x - проекція сили пружності;
k - коефіцієнт жорсткості пружного тіла;
x - величина деформації (абсолютне видовження).
Н
кг м/с2
с
м/с
м/с
Н
Н
Н/м
м
F - сила притягання тіл; |
Н |
- стала |
|
всесвітнього тяжіння; |
|
m1, m2 - маси тіл; |
кг |
r - відстань між тілами. |
м |

Сила тяжіння, вага тіла
- сила тяжіння; |
Н |
|
|
- вага тіла; |
Н |
|
|
m - маса тіла; |
кг |
= 9,8 м/с2 - прискорення |
|
вільного падіння. |
|
Сила тертя
|
Fтер - сила тертя; |
Fтер = m0N |
m0 - коефіцієнт тертя спокою; |
|
N - сила нормальної реакції. |
Елементи статики. Момент сили |
|
|
F - модуль сили; |
M = Fd |
d - плече сили; |
|
M - момент сили. |
Умови рівноваги тіла |
|
F1, F2, …, Fn - сили, що діють на тіло;
Н
Н
Н
м
Н·м
Н
M1 + M2 + … + Mn = 0 |
M1, M2, …, Mn - моменти цих |
Н·м |
|
сил. |
|
|
|
|
|
Закони збереження в механіці |
|
Імпульс тіла
Закон збереження імпульсу
(для безлічі тіл замкненої системи);
(для взаємодії двох тіл)
Механічна робота
A = F·S·cosa;
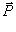 - імпульс тіла (кількість
- імпульс тіла (кількість
руху); |
|
|
m - маса тіла; |
кг |
|
- швидкість тіла. |
м/с |
|
|
||
|
- імпульси тіл |
|
замкненої системи; |
|
|
і |
- імпульси тіл до |
|
взаємодії; |
|
|
і |
- імпульси тіл після |
|
взаємодії. |
|
|
F - модуль сили, що діє на тіло; |
Н |
|

A = E2 – E 1 = DE |
S - модуль переміщення; |
|
a - кут між напрямом сили і |
|
переміщенням; |
|
A - робота сталої сили; |
|
DE - зміна енергії. |
Потужність |
|
м
рад
Дж
Дж
|
|
N - потужність; |
Вт |
|
|
|
F - модуль сили тяги; |
Н |
|
|
|
- модуль швидкості руху тіла; м/с |
||
|
|
< > - середня швидкість. |
м/с |
|
Кінетична і потенціальна енергія |
|
|||
|
|
Eк - кінетична енергія; |
Дж |
|
|
|
m - маса тіла; |
кг |
|
|
|
- швидкість тіла; |
м/с |
|
|
|
Eп - потенціальна енергія; |
Дж |
|
Eп = mgh |
|
g - прискорення вільного |
м/с2 |
|
|
|
|||
|
|
падіння; |
||
|
|
|
||
|
|
h - різниця висот. |
м |
|
Теорема про кінетичну енергію |
|
|||
|
|
А - робота тіла; |
Дж |
|
|
|
1, 2 - початкова і кінцева |
м/с |
|
|
|
швидкості тіла. |
||
|
|
|
||
Потенціальна енергія пружно деформованого тіла |
|
|||
|
|
Eп - потенціальна енергія |
Дж |
|
|
|
пружно-деформованого тіла; |
||
|
|
|
||
|
|
k - коефіцієнт жорсткості тіла; |
Н/м |
|
|
|
x - абсолютне видовження. |
м |
|
Закон збереження енергії в механіці |
|
|||
Eп1 + Eк1 = Eк2 |
+ Eп2 |
Eк - кінетична енергія; |
Дж |
|
Eп - потенціальна енергія. |
Дж |
|||
|
|
|||
Коефіцієнт корисної дії |
|
|
||
|
|
- ККД; |
|
|
|
|
Aк - корисна робота; |
Дж |
|
|
|
Aз - затрачена робота (повна |
Дж |
|
|
|
робота). |
||
|
|
|
||
|
|
Механіка рідин та газів |
|
|
Гідростатичний тиск |
|
|
||
p = rрgh |
|
rр - густина рідини; |
кг/м3 |
|

g - прискорення вільного падіння;
h - висота стовпа рідини;
р - тиск рідини на глибині h.
Закон сполучених посудин
h1, h2 - висоти стовпів рідини в стані спокою;
r1, r2 - густини рідин.
Гідравлічний прес
F1, F2 - сили, що діють на поршні;
S1, S2 - площі цих поршнів.
Закон Архімеда
м/с2
м
Па
м
кг/м3
Н
м2
|
rp - густина рідини; |
кг/м3 |
|
|
g - прискорення вільного |
м/с2 |
|
FA = rpgVт |
падіння; |
||
|
|||
|
Vт - об'єм зануреної частини |
м3 |
|
|
тіла. |
||
|
|
Під час розв'язування задач слід передусім вибрати систему відліку, яка складається із тіла відліку, пов'язаної з ним системи координат і початку відліку часу. Виконуючи рисунок до задачі, потрібно зобразити систему відліку, траєкторію руху, всі векторні величини, що визначаються умовою і положенням тіла в початковий момент часу. Далі складають кінематичні рівняння (закони) руху для кожного тіла у векторній формі і в проекціях на вибрані осі координат. У разі потреби встановлюють додаткові рівняння, які можуть виражати конкретні математичні зв'язки, що випливають з умови задачі. Отриману систему рівнянь розв'язують відносно шуканих величин.
Для графічного розв'язування задачі використовують графіки залежності від часу координат або швидкості (переміщення або шляху). Це дасть змогу визначати невідомі величини на основі графіків. Слід пам'ятати, що графічні залежності кінематичних величин можуть виявитися корисними як під час аналізу умови задачі, так і для перевірки результатів її розв'язування.

РОЗДІЛ 2. Молекулярна фізика і термодинаміка. Основні формули.
1. Рівняння стану ідеального газу:
PV = RT (для одного моля газу) PV = RT(для довільної маси газу),
де P – тиск, V- об’єм, Т – термодинамічна температура, m – маса, М – молярна маса, R – універсальна газова стала.
2. Закон Дальтона для тиску суміші газів:
= ∑ −1 ,
де Pi – парціальний тиск і-ої компоненти газу.
3. Молярна маса суміші газів:
= ∑ ,
де m – маса і-ої компоненти, - кількість молів і-ої компоненти.
4. Концентрація молекул однорідної системи:
де V – об’єм системи, - густина речовини, N – число структурних елементів системи (молекул, атомів), Na – число Авогадро.
5. Основне рівняння молекулярно-кінетичної теорії газів:
= 13 nm0( сер)2,
або:
PV = |
2 |
( |
0( сер)2 |
) = |
2 |
, |
3 |
|
3 |
||||
|
2 |
|
|
|||
де vсер. – середня квадратична швидкість молекул, m0 – маса одної молекули, N – число молекул в об’ємі газу V, n – концентрація молекул.
6.Швидкість молекул:
-найбільш ймовірна: йм = √2RT = √2kT;
0
-середня квадратична: кв = √3RT = √3kT;
0
середня арифметична: aр = √8RT = √ 8kT .
0
7.Середня кінетична енергія поступального руху молекули ідеального газу:
= 32 kT.
8.Середня кінетична енергія однієї молекули:
= 2 kT,
де і – число степенів свободи молекули.
9. Перший закон термодинаміки:
dQ + dA = dU,
де dQ – кількість теплоти, отриманої тілом, dU – зміна внутрішньої енергії, dA – робота, виконана тілом.
Молярна теплоємність:
= dQdT,

де - кількість молей (кількість речовини).
10. Молярна теплоємність газів, що складаються із n компонентів:
= 1 1+ 2 2+...+ .
11. Питома теплоємність:
dQ= dT
12. Внутрішня енергія ідеального газу:
= 2 RT
Розділ 3. Електродинаміка. Основні формули та поняття.
Електродинаміка – розділ фізики, що вивчає електромагнітне поле в найбільш загальному випадку (тобто, розглядаються змінні поля, що залежать від часу) і його взаємодію з тілами, що мають електричний заряд (електромагнітне взаємодія). Предмет електродинаміки включає зв’язок електричних і магнітних явищ, електромагнітне випромінювання (у різних умовах, як вільне, так і в різноманітних випадках взаємодії з
речовиною), електричний струм (взагалі кажучи, змінний) і його взаємодію з електромагнітним полем (електричний струм може бути розглянуто при цьому як сукупність рухомих заряджених частинок). Будь-яке електричне і магнітне взаємодія між зарядженими тілами розглядається в сучасній фізиці як здійснюване за посередництвом електромагнітного поля, і, отже, також є предметом електродинаміки.
Найчастіше під терміном електродинаміка за замовчуванням розуміється класична (не зачіпає квантових ефектів) електродинаміка; для позначення сучасної квантової теорії електромагнітного поля і його взаємодії з зарядженими частинками зазвичай використовується стійкий термін квантова електродинаміка.
Основні поняття, якими оперує електродинаміка, включають в себе:
Електромагнітне поле – це основний предмет вивчення електродинаміки, вид матерії, що виявляється при взаємодії із зарядженими тілами. Історично розділяється на два поля:
Електричний заряд – це властивість тіл, що дозволяє їм взаємодіяти з електромагнітними полями: створювати ці поля, будучи їх джерелами, і піддаватися (силового) дії цих полів.
Електричний струм – упорядкований не скомпенсований рух вільних електрична заряджених частинок, наприклад, під впливом електричного поля.
Спеціальні розділи електродинаміки

Електростатика описує властивості статичного (не мінливого з часом або мінливого досить повільно, щоб «електродинамічними» ефектами можна було знехтувати, тобто, коли в рівняннях Максвелла можна відкинути, через їх малості, члени з похідними по часу) електричного поля і його взаємодії з електрична зарядженими тілами (електричними зарядами), які також нерухомі або рухаються з досить малими швидкостями (чи, може, якщо є і швидко рухомі заряди, але вони досить малі за величиною), щоб створювані ними поля можна було наближено розглядати як статичні. Зазвичай при цьому мається на увазі і відсутність (або пренебрежимо малість) магнітних полів.
Магнітостатики досліджує постійні струми (і постійні магніти) і постійні магнітні поля (поля не змінюються в часі або змінюються настільки повільно, що швидкістю цих змін в розрахунку можна знехтувати), а також їх взаємодію.
Електродинаміка суцільних середовищ розглядає поведінку електромагнітних полів у суцільних середовищах.
Релятивістська електродинаміка розглядає електромагнітні поля в рухомих середовищах.
Основні формули електродинаміки
Закон Кулона
Різниця потенціалів
ΔU = Eδx.
Електроємність
С= q/U
Енергія конденсатора
Закон Джоуля-Ленца
ΔQ = I 2RΔt.
Сила Ампера
F = I l cos α.

Поле точкового заряду
Потенціал зарядженої кулі
Плоский конденсатор
С= ε0S/d.
Закон Ома
Сила Лоренца
F = q B sin α.
Магнітний потік
Φ= BS cos α.
Розділ 4. Коливання та хвилі. Основні формули.
4.1 Механічні коливання та хвилі.
Вільні коливання.
Рівняння гармонійних коливань:
= А(0 + 0| ), де
А– амплітуда або максимальне відхилення точки від положення рівноваги, м;0- власна частота вільних коливань;
−зміщення або відхилення точки від положення рівноваги, м;
Власна циклічна частота коливань 0 = 2 = 2Т [рад⁄с]
Частота коливань = 1Т = [Гц] Період коливань Т = 1 = [с]
Фаза коливань = 0 + 0 = 2 + 0, або при 0 = 0 = 2,
0 −початкова фаза коливань( при =0), [рад].
Швидкість при гармонійних коливаннях = ′ = А 0(0 + 0),

=А 0 - амплітуда швидкості [м⁄с] Прискорення при гармонійних коливаннях = ′ = ′′ =
−А 02(0 + 0| |
) = −02 , |
||
|
= А 2 |
= |
- амплітуда прискорення [м⁄с2]. |
|
0 |
|
0 |
Пружний маятник.
Рівняння вільних коливань пружного маятника
′′ = = − = −02 ,
−коефіцієнт жорсткості пружини [Н⁄м],−маса вантажу [кг].
Власна циклічна частота 0 = 2 = |
2 |
= √ |
|
. |
||||||||||||||||||||||||||
Т |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Період коливань Т= |
2 |
= |
|
2 √ |
|
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Потенціальна енергія п = |
2 |
|
= |
А2 |
sin2). |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|||||||||
Кінетична енергія |
= |
|
|
|
|
|
= |
|
|
0 |
A2cos2(| |0 + 0). |
|||||||||||||||||||
2 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||
Повна механічна енергія коливань |
|
|
|
|
||||||||||||||||||||||||||
|
2 |
|
|
2 |
|
|
А2 |
|
|
|
2 |
А2 |
= . |
|
|
|
|
|||||||||||||
= к + п = |
|
+ |
|
|
= |
|
|
|
|
= |
|
0 |
|
|
|
|
|
|
||||||||||||
2 |
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Амплітуда коливань А=√ |
2 |
= |
|
1 |
√ |
2 |
. |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Математичний маятник
Рівняння вільних коливань математичного маятника
′′ = = − = −02 ,
−тангенціальне прискорення [м⁄с2],−прискорення вільного падіння [м⁄с2],−довжина маятника, [м⁄с2],,
−зміщення маятника від положення рівноваги, [м⁄с2].
Вільна циклічна частота 0 = √ .
Період коливань Т=2 √ .
4.2 Електромагнітні коливання та хвилі.
Вільні коливання у електричному контурі
Рівняння вільних електричних коливань в контурі( без активного опору)
′′ = −02 .
Власна циклічна частота 0 = √1 ,
С – ємність конденсатора [Ф]; L – індуктивність контуру [Гн].
Миттєве значення заряду в конденсаторі−амплітудне значення заряду конденсатору [Кл]. Миттєве значення струму в контурі
= ′ = 0 0 = (0| |
| + |
|
). |
|
2 |
||||
|
|
|

Амплітудне значення струму в контурі |
= 0. |
||||||||
Період вільних коливань (формула Томсона) |
|||||||||
Т= |
2 |
|
|
. |
|
|
|
|
|
= 2 √ |
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
0 |
|
|
|
2 |
|
2 |
|
||
Повна енергія у контурі = Е + М = |
+ |
= , |
|||||||
2 |
|
||||||||
|
|
|
|
|
2 |
|
|||
Е −енергія електричного поля зарядженого конденсатора;М −енергія магнітного поля котушки індуктивності.
Змінний електричний струм.
Магнітний потік, пронизуючий рамку Ф= ,−площа рамки;
−кут між векторами магнітної індукції В і нормаллю к площі контуру ;−циклічна частота.
Миттєве значення ЕРС індукції у рамці
= −ф′ = −)= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Амплітудне значення ЕРС індукції |
= . |
|
|
|
|
|
|
|
|
||||||||||||
Миттєве значення змінного струму |
= (| |
|0 + 0). |
|||||||||||||||||||
ЕРС рамки, яка має витків: |
= −Ф′ |
= = , = . |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Діючи значення струму, напруги, ЕРС |
= |
|
|
|
; = |
|
; = |
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
√2 |
√2 |
|
|
√2 |
|||||||
|
|
|
|
Трансформатор |
|
|
|
|
|
|
|
|
|||||||||
Коефіцієнт трансформації |
|
1 |
|
= |
1 |
= , |
2 |
, |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
ККД трансформатора = |
2 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Індекс 1 – первинна обкладка трансформатору; Індекс 2 – вторинна обкладка трансформатору.
Розділ 5.Оптика та основи теорії відносності. Основні формули.
Геометрична оптика
Закон відбивання світла.
1) Падаючий і заломлений промені і нормаль до межі поділу лежать в
одній площині. |
|
|
|
|
|
|
|
2) |
Відношення |
синуса |
кута |
падіння α до |
синуса |
кута |
|
заломлення γ дорівнює |
відношенню |
швидкостей |
поширення світла |
в цих |
|||
середовищах: |
|
|
|
|
|
|
|
1 i |
2 – швидкості поширення світла в |
середовищах, показники |
|||||
заломлення яких п1 і п2.
Якщо світло переходить з оптично густішого середовища в оптично менш густе, то, починаючи з деякого кута падіння α0 , світло повністю відбивається від поверхні розділу цих двох середовищ. Кут падіння α, що відповідає куту

заломлення β0 = 900 , називають граничним кутом повного відбивання. В
цьому випадку γ = 900 , Sin γ = 1, отже:
Сферичне дзеркало – тіло, що має сферичну поверхню і дзеркально відбиває світло .
Рисунок 1 Оптичний центр дзеркала (О) – точка, проходячи через яку, промінь
повертається після відбивання у зворотному напрямі.
Полюс сферичного дзеркала (Р) – середина дзеркала, вершина сферичного сегмента.
Фокусна відстань (FP) – відстань від полюса дзеркала до головного фокуса F.
Головний фокус дзеркала – точка (F), у якій після відбивання перетинаються всі промені, що падають паралельно головній оптичній осі.
Головна оптична вісь – пряма (ОР), яка проходить через центр сферичної поверхні і полюс дзеркала.
Побічна оптична вісь – будь-яка пряма, що проходить через оптичний центр дзеркала.
Фокальна площина - площина, перпендикулярна до головної оптичної осі, яка проходить через головний фокус. Якщо радіус сфери R, то фокусна відстань:
Величину D, обернену до фокусної відстані, називають оптичною силою:
Вимірюється в діоптріях:

Формулою сферичного дзеркала називають таке співвідношення:
d – відстань від предмета до дзеркала, f – відстань від дзеркала до зображення, F – фокусна відстань, R – радіус сфери.
В даній формулі відстані до дійсних точок треба брати зі знаком плюс, а до уявних – зі знаком мінус.
Для побудови зображень у сферичному дзеркалі потрібно взяти будь-які з двох променів.
1.Промені АО і ВО, які проходять через центр О дзеркала (після відбивання вони протилежно направлені відносно початкового променя).
2.Промені AF i BF, які проходять через фокус F дзеркала (після відбивання вони поширюються паралельно головній оптичній осі).
3.Промені BD i AF паралельні головній оптичній осі (після відбивання від дзеркала, вони проходять через його фокус).
4.Промені АР і ВР, які падають у полюс Р дзеркала (вони відбиваються симетрично головній оптичній осі).
Рисунок 2 Лінзою називають прозоре тіло, обмежене двома сферичними поверхнями,
причому одна з них може бути плоскою. Лінза називається тонкою, якщо її товщина мала порівняно з радіусом кривизни поверхонь.
Лінза, товщина якої на краях менша, ніж на середині, називається збиральною. Лінза, краї якої товщі за середину, називається розсіювальною.
Рисунок 3

Пряма, що проходить через центри сферичних поверхонь, які обмежують лінзу, – головна оптична вісь .
Рисунок 4 Будь-яка пряма, що проходить через оптичний центр лінзи, – побічна
оптична вісь. Головний фокус лінзи – це точка, у якій після заломлення в збиральній лінзі перетинаються промені, що падають на лінзу паралельно головній оптичній осі. Фокусна відстань – відстань від оптичного центра лінзи до її фокуса. Фокальна площина – площина, яка проходить через фокус, перпендикулярна до головної оптичної осі і паралельна площині лінзи.
Для побудови зображення у лінзі потрібно використати будь-які два промені.
1.Промінь, який проходить через оптичний центр лінзи (не змінює напряму поширення).
2.Промінь, паралельний головній оптичній осі (після заломлення в лінзі йде через задній фокус).
3.Промінь, який проходить через передній фокус лінзи (після заломлення
влінзі паралельно головній оптичній осі).
Для розсіювальної лінзи передній фокус – уявний, і щоб його побудувати, беруть не самі промені, а їх продовження
Рисунок 5

Рисунок 6 Формула тонкої збиральної лінзи:
d – відстань від предмета до лінзи, f – відстань від лінзи до зображення, F – фокусна відстань, D – оптична сила лінзи.
Відстані до дійсних зображень треба брати зі знаком плюс, а до уявних – зі знаком мінус.
Відношення лінійного розміру зображення до відповідного лінійного розміру предмета називають лінійним збільшенням лінзи.
Кутове збільшення: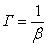
Фотометрія Світловий потік Ф – це кількість теплової енергії, що проходить через
деяку поверхню за одиницю часу.
 ,
,
де α ≤ 1 – функція видимості людського ока, яка дорівнює нулю, коли довжина хвиль λ < 0,38 мкм і λ > 0,76 мкм і дорівнює одиниці при
λ = 0,550 мкм.
Одиниця світлового потоку в СІ – люмен, 1 лм = 1кд · 1ср.
Світловий потік дорівнює добутку сили світла джерела на тілесний кут ω, в який посилають випромінювання :
Якщо джерело випромінює світло рівномірно у всіх напрямах, то сила світла:
Відношення світлового потоку Ф, що падає на поверхню площею S до цієї площі, називають освітленістю Е:

За одиницю освітленості в СІ приймають люкс (лк). Освітленість поверхні точковим джерелом прямо пропорційна силі світла джерела, косинуса кута падіння променів і обернено пропорційна квадрату відстані від джерела до
поверхні: 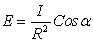 .
.
Умова максимумів: результуюче коливання максимально підсилюється тоді, коли різниця ходу додавання хвиль дорівнює парному числу півхвиль, або цілому числу довжин хвиль:
Умова мінімумів: результуюче коливання ослаблюється, якщо різниця ходу доданих хвиль дорівнює непарному числу півхвиль:
Енергія кванта E прямо пропорційна частоті світла: де h – так звана постійна Планка. h = 6,626·10–34 Дж·с. Постійна Планка – це
універсальна константа, яка у квантовій фізиці відіграє ту ж роль, що й швидкість світла в СТО.
Вимірюючи UЗ, можна визначити максимальну кінетичну енергію фотоелектронів:
Цю формулу прийнято називати рівнянням Ейнштейна для фотоефекту.
Як випливає із рівняння Ейнштейна, тангенс кута нахилу прямій, що виражає залежність замикаючого потенціалу UЗ від частоти ν, дорівнює відношенню постійної Планка h до заряду електрона e:

Це дозволяє експериментально визначити значення постійної Планка. Такі виміри були виконані в 1914 р. Р. Міллікеном і дали гарну згоду зі значенням, знайденим Планком. Ці виміри дозволили також визначити роботу виходу A:
де c – швидкість світла, λчер – довжина хвилі, відповідна до червоної границі фотоефекта. У більшості металів робота виходу A становить декілька електрон-вольт (1 еВ = 1,602·10–19Дж). У квантовій фізиці електрон-вольт часто використовується в якості енергетичної одиниці виміру. Значення постійної Планка, виражене в електрон–вольтах у секунду, дорівнює
h = 4,136·10–15 еВ·с
Серед металів найменшу роботу виходу мають лужні елементи. Наприклад, у натрію A = 1,9 еВ, що відповідає червоній границі фотоефекта λчер ≈ 680 нм. Тому сполуки лужних металів використовують для створення катодів у фотоелементах, призначених для реєстрації видимого світла.
Отже, закони фотоефекта свідчать, що світло при випромінюванні й поглинанні поводиться подібно потоку часток, що одержали назву фотонів або світлових квантів.
Енергія фотонів дорівнює
Фотон рухається у вакуумі зі швидкістю c. Фотон не має маси, m = 0. Із загального співвідношення спеціальної теорії відносності, що зв'язує енергію, імпульс і масу будьякої частки,
E2 = m2c4+p2c2,
випливає, що фотон має імпульс
.

Перетворення Лоренца мають вигляд:
Тривалість τ процесу в системі K буде дорівнювати:
Розділ 6. Атомна і ядерна фізика. Основні формули.
Перший постулат Бора (постулат стаціонарних станів) говорить: атомна система може перебувати тільки в особливих стаціонарних або квантових станах, кожному з яких відповідає певна енергія En. У стаціонарних станах атом не випромінює.
Другий постулат Бора (правило частот) формулюється в такий спосіб: при переході атома з одного стаціонарного стану з енергією En в інший стаціонарний стан з енергією Em випромінюється або поглинається квант, енергія якого дорівнює різниці енергій стаціонарних станів:
де h – стала Планка. Звідси можна виразити частоту випромінювання:

За сучасними вимірами, позитивний заряд протона в точності дорівнює елементарному заряду e = 1,60217733·10–19 Кл, тобто рівний по модулю негативному заряду електрона. У цей час рівність зарядів протона й електрона перевірено з точністю 10–22. Такий збіг зарядів двох несхожих одна на одну часток викликає подив і залишається однією з фундаментальних загадок сучасної фізики.
Маса протона, по сучасних вимірах, дорівнює mp = 1,67262·10–27 кг. У ядерній фізиці масу частки часто виражають в атомних одиницях маси (а.о.м.), яка дорівнює 1/12 маси атома вуглецю з масовим числом 12:
1 а.о.м. = 1,66057·10–27 кг.
Отже, mp = 1,007276 а.о.м. У багатьох випадках масу частки зручно виражати в еквівалентних значеннях енергії відповідно до формули E = mc2. Тому що 1 еВ = 1,60218·10–19 Дж, в енергетичних одиницях маса протона дорівнює 938,272331 МеВ.
Для характеристики атомних ядер уводиться ряд позначень. Число протонів, що входять до складу атомного ядра, позначають символом Z і називають зарядовим числом або атомним номером (це порядковий номер у періодичній таблиці Менделєєва). Заряд ядра рівний Ze, де e – елементарний заряд. Число нейтронів позначають символом N.
Загальне число нуклонів (тобто протонів і нейтронів) називають масовим числом A:
A = Z + N.
Ядра хімічних елементів позначають символом ZAX, де X – хімічний символ елемента. Наприклад,
Найважливішу роль у ядерній фізиці відіграє поняття енергії зв'язку ядра.
Енергія зв'язку ядра дорівнює мінімальної енергії, яку необхідно затратити для повного розщеплення ядра на окремі частки. Із закону збереження енергії випливає, що енергія зв'язку дорівнює тієї енергії, яка виділяється при утворі ядра з окремих часток.
Енергію зв'язку будь-якого ядра можна визначити за допомогою точного виміру його маси. У наш час фізики навчилися вимірювати маси часток –
