Добавил:

PickyEater13 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Политехнический Университет

Предмет:

Высшая математика

Файл:

Производная 1

.pdf

Скачиваний:

Добавлен:

27.11.2024

Размер:

2.09 Mб

Скачать

☆

1 / 31 2 3 > Следующая >>>

Производная функции Часть 1

Понятие производной

Пусть в промежутке [a;b] задана непрерывная функция y = f (x)

и x0 - некоторая точка в этом промежутке. Осуществим следующее построение:

1. Дадим значению аргумента x0 приращение x, т.е. переместимся из точки x0 в точку x0 x, оставаясь в пределах заданного промежутка . Значению функции в начальной

точке соответствует число	y0	= f (x0 ).
Значению функции в точке	x	x,
соответствует y = f (x0 x.) 0

2. Составим приращение функции как разность значений функции

в конечной и начальной точках.

y = f (x0 x) f (x0 )

3. Разделим приращение функции	y		f (x0 x) f (x0 )
на приращение аргумента и получим		=		,
	x		x
отношение

4. Находим предел отношения приращения функции к

приращению аргумента		lim	y	= lim	f (x0	x) f (x0 )	.
			x
		x 0		x 0		x
Этот предел и называется производной функции						y = f (x) в точке x0
	(или
и обозначается yx (x0 )		fx (x0 )) .
О п р е д е л е н и е.	Производной функции y = f (x)
называется предел отношения приращения функции к
приращению аргумента при стремлении этого приращения к
нулю				y

	yx (x0 ) = lim			x
		x 0

(в предположении, что предел этот существует).

Если этот предел существует, существует и производная в точке , и функция называется дифференцируемой в данной точке. Функция называется дифференцируемой в промежутке, если она дифференцируема в каждой точке этого промежутка.

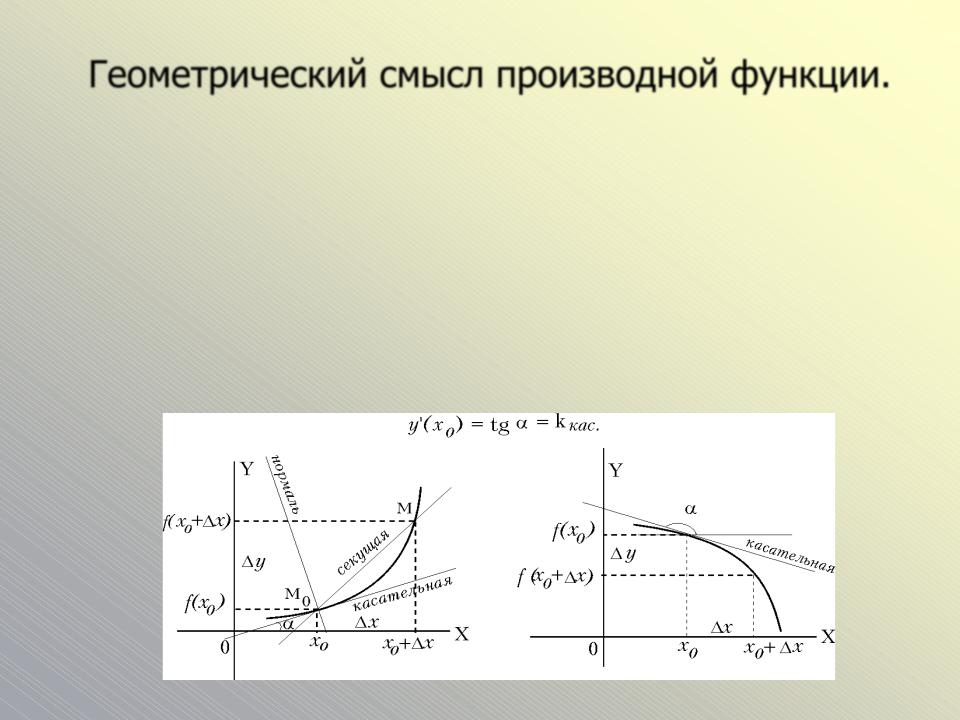
Геометрический смысл производной функции.

О п р е д е л е н и е. Касательной к графику функции y = f (x)

в точке M 0 называется предельное положение секущей M 0 M при стремлении точки M по кривой к точке M 0

Геометрический смысл производной:
Значение производной функции в точке			(x0 )
		yx
есть угловой коэффициент касательной,	проведенной к графику

функции в данной точке	(x0 ) = tg = kêàñ.
yx

Дифференцируемость функции в точке с геометрической точки зрения означает, что к графику функции в данной точке можно провести единственную невертикальную касательную (а).

Если функция недифференцируема в точке, то это означает, что касательная к графику функции в точке проходит вертикально (в, с)

	(x0 ) = tg = kêàñ.	=
= /2 yx

или в точке к графику функции можно провести больше, чем одну касательную (d) (производная не существует).

Механический смысл производной.

Производная от пройденного пути S (t) по времени t

есть мгновенная скорость прямолинейного движения в данный

момент времени t	0	S(t0 t) S(t0 )
	0
v(t0 ) = St (t0 ) = lim			.
v(t0 ) = St (t0 ) = lim			.
	t 0	t

Скорость движения в определенный момент времени также можно определить по угловому коэффициенту касательной к графику зависимости величины пройденного

Физический смысл производной

Значение производной функции в точке есть мгновенная скорость изменения функции в данной точке.

Основные правила дифференцирования

1. ( C ) = 0						Производная константы равна нулю
2.	( C U ) = C U					Константу можно вынести за знак производной
3.	( U V )' = U V					Производная суммы функций равна сумме производных
4.	( U V )' = U V U V Производная произведения двух функций
	U	'
	U			U V U V
5.			=			Производная отношения двух функций
5.			=
	V				V 2

6.		'
6.	[ y(U (x))] = yu U x
7.	xy ( y) =	1



		yx (x)

Производная сложной функции равна произведению производной функции по промежуточному аргументу на производную промежуточного аргумента по основному

Производная обратной функции есть величина обратная производной исходной функции

8. y (x) = y(x) (ln y(x))

Правило логарифмического дифференцирования

9.	UV = V UV 1	U UV lnU V	Производная показательно-степенной
			функции

Производная функции, заданной параметрически


10.		x = x(t)	,	y (x) =	y (t)	y (x) =	y (t)x (t) x (t) y (t)

					x (t)			(x (t))3
	y = y(t)				x (t)			(x (t))3

Таблица производных основных элементарных функций

1.xk ' = k xk 1

2. x ' = 2 1 x

	1	'	=	1
3.
				x2
x

4.a x ' = a x ln a

5.ex ' = ex

6. log		x ' =	1
6. log	a	x ' =	x ln a
	a

7.ln x ' = 1x

8.(sin x)' = cos x

9.(cos x)' = sin x

10.	(tg x)' =	1

		cos2 x
		cos2 x
11.	(ctg x)' =		1


		sin2 x
12.	(arcsin x)' =				1


			1		x2
			1		x2
13.	(arccos x)' =				1


					1 x2
					1 x2
14.	(arctg x)' =		1

			x2
		1	x2
15.	(arcctg x)' =				1


				1 x2

16.(sh x)' = chx

17.(ch x)' = sh x

	18. (th x)' =	1

		ch2 x
		ch2 x

1. U k ' = k U k 1 U '

U '

1 '

U '

U 2

4.aU ' = aU ln a U '

5.eU ' = eU U '

6. log U ' = 1 U '

a	U ln a

7.lnU ' = U1 U '

8.(sin U )' = cosU U '

9.(cos U )' = sin U U '

10.

(tg U )' =

U '

cos2U

11.

(ctg U )' =

U '

sin2U

12.

(arcsin U )' =

U '

U 2

13.

(arccosU )' =

U '

1 U 2

14.

(arctg U )' =

U 2

15.

(arcctg U )' =

1 U 2

16.(sh U )' = ch U U '

17.(ch U )' = sh U U '

18. (th U )' =	1		U '

	ch2	U
	ch2	U

1 / 31 2 3 > Следующая >>>

Соседние файлы в папке Модуль 6. Производная

#
27.11.2024243.96 Кб5Дифференцирование функций.docx
#
27.11.20242.09 Mб6Производная 1.pdf
#
27.11.20241.39 Mб5Производная 2.pdf
#
27.11.2024297.76 Кб9Терехина Л.И., Фикс И.И. Высшая математика -2. Глава 2. Производная функции.pdf