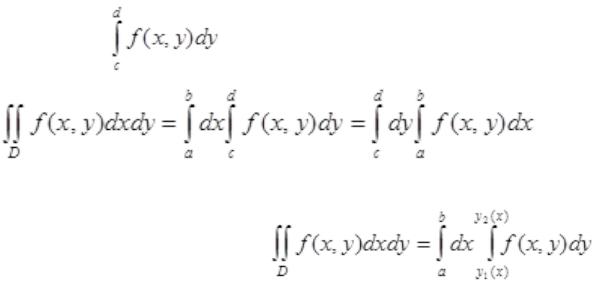
Теорема: Пусть f(x,y) интегрируема в прямоугольной |
|
области |
|
D: {a<x<b, c<y<d} и для любого x ε [a,b] существует |
|
определенный |
|
интеграл: S(x)= |
, тогда существует повторный |
интеграл: |
|
В случае криволинейной области D: {a<x<b, y1(x) <y< y2(x)} повторный интеграл равен:
1) Строит |
|
|
XOY |
интегрирования. |
в системе координат |
||||
Для вычисления двойного интеграла областьданной функции |
||||
по данной |
области рекомендуется |
действовать по |
||
2) Элементом площади является прямоугольник с размерами |
||||
следующей схеме. |
ds |
|
||
dx |
и dy |
, поэтому ds = dx dy |
|
|
3) Для заданной области |
[порядок интегрирования в соответствии со |
||||
|
|
(D) |
|
|
|
схемами 1 или 2(на следующих слайдах)] , |
|
y |
|||
определяются |
пределы изменения |
переменных |
|||
|
|
x и |
|
||
и строится соответствующий повторный (или двукратный) интеграл
Интеграл, стоящий в повторном на первом месте, называется внешним, а интеграл, стоящий после внешнего -- внутренни
)Сначала вычисляется внутренний интеграл. При этом одна из переменны x или вyзависимости от выбранного порядка интегрирования,
считается постоянной величиной
в первой из приведенных далее формул такой переменной будетy во второй -- x.
f (x, y)ds = ddy |
x |
( y) |
|
|
b |
y |
(x) |
|
|
2 |
|
f (x, y)dx |
f (x, y)ds = dx |
2 |
|
f (x, y)dy |
|||
|
|
|
|
|
|
|
|
||
(D) |
c |
x1( y) |
|
(D) |
a |
y1(x) |
|
||
5) После выполнения внутреннего интегрирования по формуле Ньютона-Лейбница внешний интеграл вычисляется как обычный определенный интеграл.
|
b |
y |
(x) |
|
f (x, y)ds = dx |
2 |
|
f (x, y)dy |
|
|
|
|
|
|
(D) |
a y1(x) |
Схема 2.
|
d |
x |
( y) |
|
f (x, y)ds = dy |
2 |
|
f (x, y)dx |
|
|
|
|
|
|
(D) |
c |
x1 |
( y) |
|
З а м е ч а н и е 1. Пределы интегрирования во внешнем интеграле всегда постоянны.
Ими служат координаты концов отрезка -- проекции области(D) на соответствующую координатную ось.
Пределы внутреннего интеграла, как правило, переменные. Они представляют собой функции, задающие границы области
Лишь в том случае, когда область представляет собой прямоугольник
о сторонами, параллельными координатным осям, ределы внутреннего интегрирования также становятся постоянными.
Удобно при расстановке пределов интегрирования использовать "стрелки", пересекающие область снизу вверх параллельно осиOY
(для 1-ой схемы расстановки пределов) или слева направо параллельно о OX (для 2-ой схемы).
Те кривые, на которой "стрелки" входят в область, называют линиями входа, а те кривые, на которой "стрелки" выходят из области, называют линиями выхода.
|
|
x2( y) |
|
|
b |
y |
(x) |
|
|
|
|
|
|
||||
|
d |
f (x, y)dx |
f (x, y)ds = dx |
2 |
|
f (x, y)dy |
||
f (x, y)ds = dy |
|
|
|
|
|
|||
|
|
|
(D) |
a |
y1(x) |
|
||
(D) |
c |
x1( y) |
|
|
||||
(D) |
«неправильная», то |
З а м е ч а н и е 2. Если область |
есть не удовлетворяет, условиям для правильной области,
например, Границы составные или прямые вертикальные или
горизонтальные пересекают её границы более, чем в двух точках, то необходимо либо поменять порядок интегрирования, либо область разбить на правильные части.
Задача 1. Записать двойной интеграл по указанной области (D) в виде повторного и расставить пределы интегрирования.
1. |
Область(D)ограничена линиями |
y = x |
2 |
и |
x y = 2. |
|
|
|
|
||||
|
Из рисунка видно, что область |
|
||||
|
ограничена сверху одной линией -- |
|||||
|
прямой |
|
x y = 2 |
|||
|
а снизу -- другой линией -- параболой |
= x2 |
||||
|
|
|
|
|
y |
|
т.е. для данной области удобно расставлять пределы интегрирования в соответствие с 1-ой схемой.
Спроектируем область на осьOX
Для нахождения абсцисс левой и правой границ области решаем систему
y = x2 |
, |
y = x2 |
, |
|
|
x2 |
= 2 x, |
|
x1 = 1, |
|
||
|
|
|
|
x, |
x2 x |
2 = 0, |
x2 |
= |
2. |
|||
x y = 2, |
y = 2 |
|
|
|||||||||
Итак, проекцией области на ось OX будет отрезок [-2;1].
Таким образом, для расстановки пределов интегрирования в повторном интеграле мы имеем:
при изменении переменнойx в интервале [ 2;1] значения переменнойyбудут находиться в пределах
от |
y1(x) = x2 - (линия входа в область) |
до |
y2 (x) = 2 x (линия выхода). |
Запишем повторный интеграл
|
b |
y |
(x) |
1 |
2 x |
|
|
f (x, y)dx dy = dx |
2 |
|
f (x, y)dy = dx |
|
f (x, y)dy. |
||
|
|
|
|
|
|
||
(D) |
a |
y1(x) |
2 |
x2 |
2. Область (D)ограничена линиями:
x y2 = 12 и |
x 4y = 0. |
1) Построим область (D.) Она ограничена справа параболой
x y2 |
= 12 |
y2 |
= (x 12) |
|
с вершиной в точке |
O (12; 0) |
|
||
|
и ветвями, направленными влево, |
|||
и слева прямой |
x 4y = 0 |
x = 4y |
||
для данной области удобно расставлять пределы интегрирования согласно 2-ой схеме
|
d |
x |
( y) |
|
f (x, y)ds = dy |
2 |
|
f (x, y)dx |
|
|
|
|
|
|
(D) |
c |
x1( y) |
|
|
Спроектируем область на ось OY.
Для нахождения ординат нижней и верхней точек области решаем систем
x y2 = 12, |
x = 12 y2 |
, |
|
12 y2 = 4y, |
|
y1= 2, |
|
|
|
y2 4y 12 = 0, |
y2 = 6. |
||
x 4y = 0, |
x = 4 y, |
|
|
|
||
Итак, проекцией области на ось |
OYбудет отрезок [ 2; 6]. |
|||||
аким образом, для расстановки пределов интегрирования в повторном |
|||||||||
нтеграле мы имеем: при изменении переменнойy в интервале [ 2; 6]. |
|||||||||
|
x |
|
|
|
|
|
|
|
|
значения переменной будут находиться в пределахот x1( y) = 4y |
|||||||||
(линия входа в область) до |
|
|
|
2 |
(линия |
|
|
|
|
|
x2 ( y) = 12 y |
|
выхода). |
12 y2 |
|
||||
апишем повторный |
|
d |
x ( y) |
|
|
6 |
|
||
f (x, y)dx dy = |
dy |
2 |
f (x, y)dx = |
dy |
|
f (x, y)dx. |
|||
интеграл |
|
|
|
|
|
|
|
||
|
(D) |
c |
x1( y) |
|
|
2 |
4 y |
|
|