
- •Тема III : Функции многих переменных.
- •Тема III: Функции нескольких переменных.
- •Глава 1. Предел и непрерывность ФНП.
- •ГЛАВА III ПРИЛОЖЕНИЯ ПРОИЗВОДНЫХ И
- •§2. Производная по направлению. Градиент.
- •§ 3. ПРИМЕНЕНИЕ ПОЛНОГО ДИФФЕРЕНЦИАЛА К
- •Приближенные вычисления с помощью дифференциала
- •откуда окончательно получаем формулу приближенных вычислений
- •Задача. Заменяя полное приращение функции ее дифференциалом, вычислить приближенно значение функции
- •4)Все полученные значения подставляем в формулу приближенных вычислений
- •ГЛАВА IV ЭКСТРЕМУМЫ Ф.Н.П.
- •Экстремум функции двух переменных
- •Необходимый признак экстремума
- •То, что условия (*) не являются достаточными легко
- •§2. Достаточные условия экстремума
- •Задача. Исследовать на экстремум функцию
- •3) Находим частные производные второго порядка и вычисляем их в этих точках
- •§ 3. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ
- •Пример . Найти наибольшее и наименьшее значения функции z x2
- •Пример: Найти наибольшее и наименьшее значения
- •Тема IV. : КРАТНЫЕ ИНТЕГРАЛЫ
- •§2. Понятие двойного интеграла
- •О п р е д е л е н и е. Двойным интегралом

§ 3. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ
ФУНКЦИИ В ОБЛАСТИ.
Пусть функция z f (x, y) определена и непрерывна со своими
частными производными 1-го порядка в замкнутой области D Тогда она согласно теореме Вейерштрасса достигает своего
наибольшего и наименьшего (т.е. глобального максимума и минимума)
значения либо во внутренних точках области, либо на границ этой области. Если экстремальное значение функция принимает во внутренних точках области, то эти точки обязательно будут критическими.
Поэтому для отыскания наибольшего и наименьшего значений в замкнутой области D необходимо:
1.Найти стационарные точки в этой области и вычислить значения функций в них.
2.Найти наибольшее и наименьшее значения функции на границах области, т.е. найти условный экстремум, например, методом исключения. Для этого из уравнений границы выражаем одну из переменных и подставляем в функцию z f (x, y). В результате получаем функцию
одной переменной, заданной на отрезке.
3.Из всех полученных значений функции нужно выбрать наибольшее и наименьшее.
Пример . Найти наибольшее и наименьшее значения функции z x2 |
y2 в |
||||
круге x2 y2 1. |
|
|
|
||
Решение: Находим частные производные: |
|
|
|
||
|
z |
2x; |
z |
2y . |
|
|
|
y |
|
||
|
x |
|
|
||
Приравнивая эти производные нулю, получим систему уравнений
2x 0,
2y 0,
откуда х = 0, у = 0; т.е. имеется одна критическая точка (0; 0).
Найдем критические точки функции на границе области – окружности, задаваемой уравнением x2 y2 1. Подставляя y2 1 x2 в функцию z=z(x; y), получим функцию одной переменной z = x2 – 1 + x2 = 2x2 – 1, причем x [–1; 1].
Найдя производную z = 4x и приравнивая ее к нулю, получим критическую точку на границе области х = 0. Найдем значения функции z=z(x; y) в критических точках внутри области z(0; 0) = 0 и на ее границе z(0) = –1, а также на концах отрезка [–1; 1] на границе области z(–1) = =z(1)= 1 и выбираем среди них наибольшее и наименьшее.
Итак, zнаиб = z(–1; 0) = z(1; 0) = 1 и zнаим = z(0; 1) = z(0; –1) = –1.
Пример: Найти наибольшее и наименьшее значения
функции z 2x2 2xy y2 /2 4y в замкнутой области D, ограниченной линиями: {y 2x; y 4; x 0}.
1. Находим критические точки:
zx 4x 2y 0; zy 2x y 4 0.
M : x 1; |
y 2 D. |
z(M ) z(1; 2) 4. |
2. z(O) 0; |
z(A) 8; |
z(B) 0. |
3. OA: x=0 z y2 /2 4y. |
||
zy y 4 0; y 4 точка A, z 8 AB: y 4; z 2x2 ( 8x) 8 16
zx 4x 8 0; x 2; y 4. точка B
OB:
y 2x; z 2x2 4x2 4x2 /2 8x
4x2 8x; zx 8x 8 0; x 1; y 2. точка М z 4.
zmin 0; в точках BиО. zmax 8 в точке А.
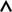 y
y
2
0 x
|
M |
A -4 |
B |

Тема IV. : КРАТНЫЕ ИНТЕГРАЛЫ
Глава 1. Двойные интегралы и их вычисление.
В данной теме мы рассмотрим основные вопросы интегрирования функций многих переменных и обобщение понятия определенного интеграла для функций нескольких переменных.
§1. Примеры, приводящие к понятию кратного интеграла.
Рассмотрим тело (T), плотность ρ, которого известна, но переменна. Требуется вычислить массу m этого тела. Повторим схему, аналогичную схеме построения определенного интеграла: 1) разобьем тело на элементарные части (кусочки-объемчики); 2) выберем в каждом по точке; 3) приближенно подсчитаем массу кусочка, как произведение плотности на объем и 4) просуммируем. Получим приближенно массу тела, а в пределе, если он существует, получим точное равенство.
m limn in=1 p(Mi ) Ti
(1.1)
Этот предел называют кратным интегралом. Смысл кратности интеграла связан с размерностью области T.

§2. Понятие двойного интеграла
Двойной интеграл является логическим продолжением понятия определенного интеграла на случай функции двух независимых переменных по плоскойПусть вобластизамкнутой. области(D) плоскости XOY
определена функция z = f (x, y) .
Повторим схему, аналогичную схеме построения определенного интеграла Разобьем область(Dпроизвольной) сеткой линий на элементарныечасти
si (i = 1,2, nи) вычислим значения функции в произвольной точке
(xi ,каждойyi ) элементарной области и составим интегральную сумму.
Оп р е д е л е н и е. Интегральной суммой для функцииz = f (x, y)
называется сумма произведений значений функции в выбранных точках на площади соответствующих
частичных (элементарных) областей
in=1 f (xi , yi ) si.
О п р е д е л е н и е. Двойным интегралом от функцииz = f (x, y)
по области (называетсяD) предел полученной интегральной суммы при неограниченном увеличении числарзбиений области на части
и стремлении площадей всех элементарных участков к нулю
f (x, y)ds = limn in=1 f (xi , yi ) si
(D)
Если такой предел существует, то функция f(x,y) называется интегрируемой в области D. Всякая непрерывная в ограниченной замкнутой области D функция f(x,y) интегрируема на ней.
Геометрически двойной интеграл от неотрицательной в области D функции z = f(x; y) есть объем цилиндрического тела, ограниченного сверху графиком поверхности z = f(x; y), снизу – областью D в плоскости x0y и с боков – цилиндрической поверхностью с образующими, параллельными оси 0z.
$2. Свойства двойного интеграла.
1. Вынесение постоянного множителя за знак интеграла
cf ( p)ds c f ( p) ds .
D D
2. Почленное интегрирование
f1( p) f2 ( p) ds f1( p)ds f2 ( p)ds .
D D D
3. Аддитивность (разбиение области на части). Если область D состоит из областей D1, D2, ..., Dn, то
f ( p)ds |
f ( p)ds |
f ( p)ds ... |
f ( p)ds . |
|
|
|
|
D |
D1 |
D2 |
Dn |
4. Если в области D имеет место неравенство f1(p) f2(p), то
f1( p)ds f2 ( p)ds
D1 D2
5. Оценка двойного интеграла. Если М и m – соответственно наибольшее и наименьшее значения функции f(p) в области D, то
m S f ( p)ds M S ,
D
где S – площадь области D.
Теорема о среднем значении. Если функция f(p) – непрерывна в области D, то двойной интеграл равен произведению значения функции
в некоторой точке Pc области интегрирования на площадь этой области:
f ( p) ds f (Pc ) S /
D
