Криволинейный и поверхностный интегралы, элементы теории поля. Таблица формул.
Тип интеграла
1Криволиней-
ный
1-го рода (по длине дуги)
2Криволиней-
ный 2-го рода (по
координатам
Формула
Грина
3Поверхност-
ный 1-го рода (по площади)
4Поверхност-
ный 2-го рода (по
координатам
Вид интеграла
f (x, y)dl
L
Fdr
AB
Pdx Qdy.
AB
F {P, Q}
Pdx Qdy
L
f (x, y, z)ds
S
П (F , n) ds
S
Pdydz
S
Qdxdz Rdxdy.
F {P,Q, R}
R(x, y, z)dxdy
S
P(x, y, z)dydz
S
Уравнение линии,
поверхности
x x(t), y y(t) ( t )
y y(x) (a x b)
( ) ( )
x x(t), y y(t)
tA ; tb y y(x)
a xA ,b xB L граница области G
z z(x, y)
Gxy проекция S на X 0Y
S (x, y, z) 0 [z z(x, y)]
Gxy проекция S на X 0Y
Формула для вычисления
f [x(t), y(t)]
(xt )2 ( yt )2 dt
b |
|
|
|
|
f [x, y(x)] 1 ( y )2 dx |
||||
|
x |
|
|
|
a |
|
|
|
|
|
|
|
|
|
f ( cos , sin ) |
2 ( )2 d |
|||
|
|
|
|
|
(P[x(t), y(t)] xt Q[x(t), y(t)] yt )dt
b
(P[x, y(x)] Q[x, y(x)] y )dx
x
a
( |
Q |
|
P )dxdy |
|
|
|
|
|
y |
|
|
|
|
G |
x |
|
|
|
||
|
f [x, y, z(x, y)] 1 (z )2 |
(z )2 dxdy |
||||
|
|
|
x |
y |
||
Gxy
П(Pcos Qcos Rcos )ds
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
PSx |
QSy |
RSz |
|
||
|
|
|
|
|
|
|
|
|
| S | |
|
|
||
|
|
|
|
|
|
dxdy |
|
|
|
|
|
| z z ( x, y ) |
|
|
Gxy |
|
z |
|
|
z z(x, y) |
R[x, y, z(x, y)] |
|
cos |
dxdy |
|
|
| cos | |
||||
|
|
|
|
||
|
Gxy |
|
|
|
|
x x(x, y) |
P[x( y, z), y, z)] |
cos |
|
dydz |
|
|
| cos | |
||||
|
|
|
|
||
|
Gxy |
|
|
|
|
Формула
Стокса
Формула
Остроградс- кого-Гаусса
Pdx Qdy Rdz |
LS граница S, |
||||
|
опирающейся на LS |
||||
LS |
|||||
|
|
|
|
|
|
Ц (F , dr) |
(rot F , n)ds |
||||
|
LS |
|
|
S |
|
Pdydz |
V область, |
|
|||
|
ограниченная S |
|
|||
S |
|
||||
Qdxdz Rdxdy |
|
|
|
|
|
П |
|
|
|||
|
(F , n) ds |
div Fdv |
|||
|
Q |
|
P |
|
R |
|
|
|
dxdy |
|
|||
|
|
|
|
|
|
|
|
x |
|
y |
|
||
S |
|
y |
|
|
||
|
P |
|
R |
|
|
|
|
z |
dzdx |
|
|
|
|
|
|
x |
|
|
|
|
|
P |
|
Q |
|
R |
|
|
|
dxdydz |
||
|
|
|
|
|
|
|
x |
|
y |
|
|
V |
|
|
z |
||
Q
dydz
z
SV
Ротор (вихрь) поля
О п р е д е л е н и е. Ротором, или вихрем, векторного поля
A = {P,Q, R}в некоторой точке называется вектор |
|
|
||||||||||||||||||
|
i |
|
j |
k |
|
|
R |
|
Q |
|
P |
|
R |
|
Q |
|
P |
|||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
rotA = |
|
|
|
|
|
|
|
= |
|
|
|
, |
|
|
|
, |
|
|
|
|
|
x |
|
y |
|
z |
y |
z |
z |
x |
x |
y |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
P |
Q |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторный определитель раскрывается как и обычный числовой. Необходимо только иметь ввиду, что произведение, например,
|
Q |
|
Q следует понимать как производную |
. |
|
x |
x |
|
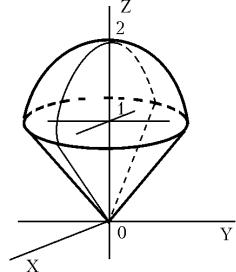
Найти поток поля |
A = {x2/2 2x 1, 3cos z 6y, ey 4z} |
|||||
через внешнюю сторону замкнутой поверхности |
||||||
|
|
x2 y2=2 z, x2 y2 = z2. |
|
|||
Найдем дивергенцию поля |
|
|
|
|||
|
2 |
/2 2x 1) |
(3cos z 6y) (e |
y |
4z) |
= x 2 6 4 = x. |
divA = |
(x |
|
||||
|
|
x |
y |
z |
|
|
П = |
|
|
div A dv = |
x dv. |
|
|
(V ) |
(V ) |
Дивергенция поля не является величиной постоянной, поэтому в данной задаче необходимо решить тройной интеграл от функции дивергенции по объему.
Для решения интеграла перейдем к цилиндрическим координатам:
x = cos , |
y = sin , |
z = z, dv = dxdydz = d d dz, |
Записываем уравнения поверхностей, ограничивающих тело в цилиндрической системе координат
Сверху тело ограничено параболоидомx2 y2 |
= 2 z z = 2 2 , |
||||||
а снизу - конусом x2 y2 = z2 |
|
z = , |
|
|
|||
Таким образом, пределы интегрирования |
|
|
|
||||
2 2 = = 1, z 2 2 , 0 2 , 0 1. |
|||||||
|
|
2 |
|
1 |
2 2 |
|
|
|
П = |
|
|
|
cos dz = |
||
|
|
d |
d |
|
|||
|
|
0 |
|
0 |
|
|
|
|
2 |
|
|
1 |
|
2 2 |
|
|
|
|
|
|
|
|
dz = 0. |
|
cos d 2 d |
|
|||||
|
0 |
|
|
0 |
|
|
|
|
Не проводя вычислений внутренних интегралов, |
||||||
|
можно сделать вывод, что интеграл равен нулю, |
||||||
2
так как cos d = sin |02 = 0.
0
Скалярное поле
XOY |
задано, |
Скалярное поле в некоторой области плоскости |
сли в каждой точке этой области определена некоторая функция двух |
|
езависимых переменных |
U = f (x; y). |
|
|
Скалярное поле в некоторой области 3-х мерного пространства задано,
если в каждой точке этого пространства определена некоторая функция трех независимых переменных
U = f (x; y; z).
Физическими примерами скалярных полей могут служить
-- поле температур неравномерно нагретого телаT=T (x; y; z),
-- поле атмосферного давления на некотором участке земной поверхности
P = P(x; y),
--поле распределения высоты поверхности над уровнем моряH = H (x; y),
--потенциал электрического или магнитного поля вокруг проводника с то
= (x; y; z).
Основные характеристики скалярных полей
1.Линии и поверхности уровня.
2.Производная поля в точке в заданном направлении.
3.Градиент поля.
Линии и поверхности уровня
U = U (x; y) |
называется линия на |
Линией уровня скалярного поля |
плоскости, соединяющая точки равных значений функции,
т.е. семейство линий уровня на плоскости определяется уравнением
U (x; y) = const.
В случае пространственного поля говорят о поверхностях уровня – -поверхностях, на которых функция принимает одинаковые значения. равнения поверхностей уровня:
U (x; y; z) = const.
Физические примеры линий и поверхностей уровня:
--изотермы, изобары в метеорологии,
--горизонтали в картографии,
--эквипотенциальные линии и поверхности в теории электромагнетизма.
Задача. Найти и изобразить линии и поверхности уровня скалярных пол
1. U = x2 y2.
Семейство линий уровня определяется уравнением
x2 y2 = C, |
|
|
x2 |
|
y2 |
= 1. |
|
C |
C |
||||
|
|
|
|
|
||
Это семейство равнобоких гипербол |
|
|||||
с асимптотами y = x, |
y = x. |
|
|
|||
В зависимости от знака взятой константыC действительной осью гипербол может быть и ось OX , и ось OY.
Производная по направлению
Пусть в некоторой области 3-х мерного пространства, содержащей точку M0 (x0; y0; z0задана), дифференцируемая функцияU = U (x; y; z).
Проследим за ее изменением при перемещении из точкиM0 (x0; y0; z0 )
взаданном направлении, характеризуемом единичным векторомl,
,OZ углы , ,образующим с осями координатOX , OY
соответственно.
О п р е д е л е н и е.
Производной скалярной функцииU (x; y; z) по направлениюl в точке M0 (x0; y0; z0 )
называется конечныйпредел отношения приращения функции U при перемещении
из точки M0 (x0; y0; z0 )в направлении вектора lк величине этого перемещенияρ
при стремлении величины перемещения к нулю
Ul = lim 0 U .